Flussi di Cassa Indipendenti o Perfettamente Correlati

Si può dimostrare che sotto tale ipotesi, la varianza è calcolabile come:

i flussi di cassa sono perfettamente correlati: date quindi le entrate di cassa all'anno 1, tutte le successive entrate sono influenzate dal trend seguito negli anni precedenti. Esiste quindi una relazione che regola la successione dei flussi di cassa.

La varianza si esprime come:

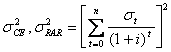
Vediamo ora, attraverso un esempio, come la conoscenza di s sia utile nella valutazione della bontà di un progetto.

Esempio

L'azienda "Giordanix SpA" sta valut 939e41j ando il progetto "Delta", che presenta un costo iniziale di 300M£ e la seguente distribuzione delle entrate di cassa:

dove:    R = valore atteso [M£] P = probabilità di accadimento dell'evento

L'azienda assegna i sseguenti valori del Coefficiente di Certezza Equivalente:

a

a

a

Si valuti:

l'equivalente certo del progetto, assumendo un tasso di sconto risk-free del 6%

la deviazione standard s_CE nel caso di flussi di cassa indipendenti e perfettamente correlati

il coefficiente di variazione per entrambe i casi

Soluzione

Calcoliamo come primo passo i valori attesi R^* nei vari periodi.

R^*₁ = 80M£ (0,1) + 100M£ (0,2) + 120M£ (0,4) + 140M£ (0,2) + 160M£ (0,1) = 120 M£

analogamente si ha:   R^*₂ = 132 M£ R^*₃ = 138,8 M£

Valutiamo l'Equivalente Certo:

Deviazione Standard dei valori attesi nei periodi

Essendo:

s _A =

svolgendo i calcoli risulta :

s = 21,9 M£

s = 19,39 M£

s = 14,09 M£

Valutazione di s_CE per

a.   FC indipendenti

b.   FC perfettamente correlati

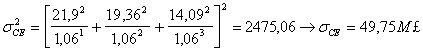
Coefficiente di variazione u

Essendo risulta :

FC indipendenti u

FC perfettamente correlati u

Considerazioni Conclusive: il progetto Delta presenta un CE>0 quindi rispetta il criterio di accettabilità. E' però interessante notare come il valore di s_CE nel caso di entrate di cassa perfettamente correlate sia significativamente maggiore di s_CE qualora i flussi di cassa siano ipotizzati indipendenti. Questo è dovuto alla risultante intensificazione del rischio prodotta dalla stretta correlazione esistente tra i flussi di cassa lungo la vita del progetto (l'andamento dei flussi negli anni precedenti influenza pesantemente il valore assunto nell'anno successivo), mentre nel caso di flussi indipendenti la correlazione è nulla, cioè quello che accade in uno specifico anno né influenza, né è influenzato dallo scenario degli anni precedenti e successivi.

4.6. Applicazione del modello CAPM in condizioni di incertezza e rischio

Una evoluzione del modello CAPM può essere impiegata per valutare la bontà di progetti inseriti in un mercato "incerto" e rischioso.

Il metodo si basa su due principi fondamentali :

Il ritorno atteso di ogni progetto è messo in relazione ad un indice che rappresenta il ritorno medio previsto dal mercato economico visto nella sua globalità

l'accettabilità del progetto si ricava dal confronto tra i valori stimati del Ritorno Atteso e del Ritorno Richiesto: se il ritorno atteso è maggiore di quello richiesto dal progetto per ripagarsi, allora l'investimento viene accettato.

La Tabella A riporta i valori previsti dalle varie grandezze nei diversi scenari, dove:

P_s = probabilità di avvenimento di ogni scenario dello stato economico

R_m = indice di ritorno di mercato (attività economica vista nella sua globalità)

R_a,...,d = indici di ritorno di ogni progetto

Tabella A

Punto 1 : valutazione del Ritorno Atteso, della Varianza e della Deviazione Standard di ogni progetto

Determiniamo tutte queste grandezze sia per il mercato che per i singoli progetti. Nella tabella sotto sono riportati i calcoli nel caso di analisi del mercato :

Tabella B

dove :   E (Rm) = valore atteso

s² _m = varianza

s _m = deviazione standard

Analogamente si procede per i progetti a, b, c, d ; si ottine così :

E (Ra) = 0.159

E (Rb) = 0.200

E (Rc) = 0.230

E (Rd) = 0.080

Punto 2 : valutazione del Ritorno Richiesto di ogni progetto

Il ritorno richiesto è legato alla rischiosità dell'investimento; il modello CAPM propone di valutarlo attraverso l'espressione:

RR _j = r _r-f + [E(Rm) - r _r-f ] B _j

dove :   RR _j = ritorno richiesto dal progetto j

r _r-f = tasso risk-free

E(Rm) = ritorno atteso valutato in base all'indice di ritorno del mercato

B _j = coefficiente beta del progetto j, definito dall'equazione:

Bj = [Cov (Rj , Rm)] / s² _m

in cui :  Cov (Rj , Rm) = covarianza tra i ritorni del progetto j e quelli dell'indice di mercato m

s² _m = varianza dell'indice di mercato

Nella tabella sotto, sviluppiamo i calcoli per il progetto a :

Tabella C

da cui :

Ba = [Cov (Ra , Rm)] / s² _m

Il prospetto relativo ai quattro progetti è :

Ricavati questi valori, supponendo un tasso risk-free dell' 8%, calcoliamo il ritorno richiesto attraverso l'espressione

RR _j = r _r-f + [E(Rm) - r _r-f ] B _j

e lo confrontiamo con il ritorno atteso.

Il criterio di accettabilità è: se il ritorno atteso è pari o supera il ritorno richiesto il progetto viene accettato, viceversa viene scartato; nel caso in esame solo il progetto a deve essere accettato, infatti tutti gli altri tre progetti presentano un ritorno atteso E(Rj) minore del ritorno richiesto RRj.