Distribuzione del Chi-square

economia

Distribuzione del Chi-square

E' molto utile per testare la "bontà" di un fit tra dati sperimentali e dati teorici. Matematicamente può essere  così definita: date n variabili indipendenti , con distribuzione Gaussiana, con valore teorico e deviazione standard , la somma:

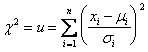838f58i 838f58i 838f58i 838f58i 838f58i 838f58i     (1)

definita come Chi-square (Chi-quadro). Nelle notazioni, per evitare ambiguità negli esponenti useremo sempre

Se è una variabile casuale, è anch'essa una variabile casuale e si può mostrare che segue la distribuzione:

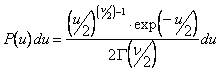838f58i 838f58i 838f58i 838f58i 838f58i     (2)

dove è la funzione gamma e è un integrale che corrisponde ai gradi di libertà ed è l'unico parametro della distribuzione. Il suo valore determina la forma della distribuzione. I gradi di libertà possono essere interpretati come parametri in relazione con il numero n di variabili della somma (1). In particolare se conosciamo il numero n di variabili indipendenti e il numero m di parametri bloccati dalla formula (m=2 nel caso y=ax+b) allora

La figura 1 indica la distribuzione del chi-square per vari valori di . Si può dimostrare che il valor medio e la dev. standard di una variabile distribuita come il chi-square a gradi di libertà sono:

Per vedere cosa rappresenta il chi-square, osserviamo la (1). Ignorando per un momento l'esponente, ogni termine nella somma è la deviazione di dal valore teorico, diviso per la dispersione. Perciò il chi-square caratterizza le fluttuazioni nei vari . Se infatti gli hanno distribuzione Gaussiana, con i parametri indicati, allora in media, ogni rapporto dovrebbe essere circa 1 e il

Per ogni dato insieme di , naturalmente, ci sarà una fluttuazione di da questa media () con una probabilità data dalla (2). L'utilità di questa distribuzione è che può essere usata per testare le ipotesi. Dal disporsi del chi-square tra un dato sperimentale e una media teorica, si può ottenere una misura della ragionevolezza delle fluttuazioni del dato sperimentale da questa media teorica. Se si ottiene un valore improbabile del chi-square, allora bisogna riesaminare i parametri teorici usati.

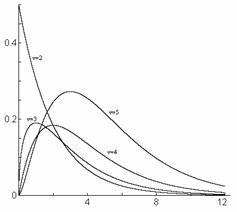Figura 1

Una volta trovato un valore di , ci possiamo chiedere quale sia la probabilità che un altrosia maggiore (ovvero che il ridotto sia più vicino a 1).

Esempio: Facendo i conti trovo che =2.08 con 4 gdl. Il ridotto

Che probabilità ho di avere in futuro misure con un più grande ovvero più vicino a 1? E' sufficiente calcolarla tramite la (2):

Se trovo che la probabilità è alta, allora significa che il mio fit è buono; altrimenti ho fluttuazioni troppo grandi, e mi conviene cambiare fit.