|
|
| |
LA QUANTITA' DI MOTO
Dobbiamo ora affrontare il problema della definizione in meccanica quantistica della quantità di moto.
Un modo naturale di procedere eè quello di richiedere alla nuova teoria probabilistica che 616g65g dare previsioni per l'evoluzione delle grandezze fisiche che siano in accordo in "media" con le previsioni della meccanica classica.
E' facile ad esempio derivare dall'equazione di Scrodinger una equazione di evoluzione per la posizione media e confrontare con l'equazione di evoluzione classica.
![]() (1)
(1)
Dalla prima utilizzando l'equazione di Scrödinger si ottiene
 (2)
(2)
Con un procedimento di integrazione per parti possiamo semplificare l'espressione. Prendendo ad esempio in considerazione il secondo termine si ottiene dopo una prima integrazione
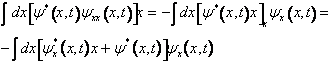 (3)
(3)
Si noti come le "parti finite ", che intervengono nella formula della integrazione per parti, siano state trascurate perchè la condizione di normalizzazione implica che le ampiezze di probabilità tendano a zero con le loro derivate per x che tende in modulo all'infinito. Il primo termine è il complesso coniugato del termine considerato e pertanto si ha complessivamente
![]() (4)
(4)
Possiamo interpretare questo risultato in due modi.
a)Eseguiamo un'altra integrazione per parti ottenendo
![]() (5)
(5)
Il secondo membro si interpreta come la media di un operatore differenziale quantità di moto
![]() (6)
(6)
La regola per ottenere la media di un operatore è quella di far agire l'operatore differenziale sulla ampiezza di probabilità, moltiplicare poi per l'ampiezza di probabilità complessa coniugata ed integrare.
Con questa definizione di quantità di moto come un operatore e la regola per definire la media dell'operatore si verifica la legge del moto classica.
b)Esiste un modo alternativo a prima vista più naturale. Esprimiamo l'ampiezza di probabilità come prodotto di un modulo ed una fase.
![]() (7)
(7)
Sostituendo nella ( ) si ottiene
![]() (8)
(8)
L'interpretazione è quella che il gradiente della fase cambiato di segno e diviso per la massa definisce ad ogni istante un campo di velocità la cui media (il quadrato di A è la densità di di probabilità) moltiplicata per la massa esprime la quantità di moto media. La quantità di moto risulterebbe pertanto una funzione dello spazio e del tempo definita associata al gradiente della fase della ampiezza di probabilita'.
Tale definizione e' equivalente alla precedente per quel che riguarda il calcolo del valor medio, ma porta ad una diversa valutazione del momento del secondo ordine. Dalla prima definizione abbiamo infatti,
![]() (9)
(9)
Operando una prima integrazione per parti otteniamo
![]() (10)
(10)
introducendo modulo e fase si perviene al seguente risultato.
![]() (11)
(11)
La seconda definizione ci darebbe invece solo il secondo termine e di conseguenza un secondo momento nullo nel caso di ampiezze di probabilita' reali. Questo e' in contraddizione almeno con il principio di Heisenberg che afferma che per un qualsiasi stato quantistico il prodotto delle incertezza sulla quantita' di moto per l'incertezza sulla posizione e' sempre maggiore di zero.
![]() (12)
(12)
Per incertezza intendiamo la media del quadrato della differenza tra la grandezza stessa ed il suo valor medio.
![]() (13)
(13)
Nel caso di valori medi nulli l'incertezza coincide con il momento del secondo ordine.
Il principio trae origine dalla critica al postulato classico che assumeva posizione e quantita' come grandezza determinabili con precisione indipendente. Una semplice analisi dei dispositivi anche ideali atti a determinare queste grandezze ci convince infatti che tale postulato non e' verificabile almeno nell'ambito dei procedimenti di misura attualmente concepibili. La difficolta' e' legata alla natura natura corpuscolare della radiazione elettromagnetica per cui la localizzazione di una particella con una incertezza dell'ordine della lunghezza d'onda implica una cessione di quantita' di moto alla particella dell'ordine di grandezza della quantita' di moto inversamente proporzionale alla lunghezza d'onda e pertanto una incertezza sulla quantita' di moto inversamente proporzionale alla incertezza sulla posizione. Heisenberg trasse spunto da questa critica alla meccanica classica per ipotizzare che in una formulazione alternativa la relazione di indeterminazione dovesse assumere il carattere di postulato. Le grandezze fisiche posizione e quantita' e le medie relative dovevano cioè essere definite in modo da verificare la relazione di indeterminazione.
Prima di vedere in generale quale deve essere la relazione tra due grandezze affinchè sia verificata una relazione di indeterminazione vogliamo verificare la relazione stessa nei due casi particolari che abbiamo introdotto.
Nel caso della diffusione quantistica se ass
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025