|
|
| |
Consideriamo le distribuzioni dlella componente X condizionate ai diversi valori della componente Y. Ovvero suddividiamo la popolazione in esame in gruppi con altezza appartenenti alla stessa classe (il gruppo di altezza 1.65, quello di altezza 1.75 e cosi' via) e calcoliamo la distribuzione delle altezze in ciascun gruppo. Se il risultato di tale indagine porta a distribuzioni significamente diverse in ciascun gruppo: ad esempio che la frequenze dei pesi piu' bassi siano maggiori nei gruppi con altezza minore, mentre le frequenze dei pesi piu' alti siano maggiori nei gruppi con pesi maggiori, si puo' supporre che tra le componenti della variabile esista una dipendenza. Viceversa se le cio' non si verifi 626h74g ca, si puo' supporre che le due componenti siano indipendenti.
Se riportiamo sul piano cartesiano x,y le coppie di valori ottenuti da un'idagine statistica, ci aspetteremo che i dati siano distribuiti in maniera omogenea nelle due direzioni x,y nel caso di indipendenza, e che seguano una certa legge nel caso di dipendenza.
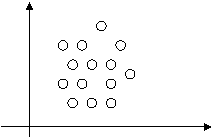
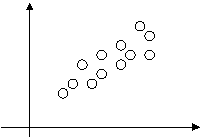
Torniamo ai dati non ordinati che abbiamo raccolto sulla popolazione di 10 individui. Avendo registrato per ciascun individuo due caratteristiche, la media sara' un vettore a due componenti: la prima sara' la media della caratteristica X e la seconda la media della caratteristica Y. La media della componente X si otterra' come media aritmetica dei valori che essa assume nella popolazione, eanalogamente la media della componente Y sara' la media aritmetic adei valori assunti dalla Y nella popolazione. Cio' equivale a considerare separatamente le due componenti, ordinarle nelle distribuzioni marginali, o ricavare le distribuzioni marginali a partire dalla distribuzione congiunta nella tabella a doppia entrata, e calcolare separatamente le due componenti della media come nel caso monodimensionale.
![]()
![]()
Ricordando l'espressione delle marginali si ottiene che
![]()
![]()
Cio' ci permette di definire l'operatore media per le variabili statistiche a due dimensioni:
![]()
Nel caso in cui si faccia la media di una delle due componenti o di una sua funzione si puo' utilizzare la distribuzione di frequenza marginale di tale componente:
![]()
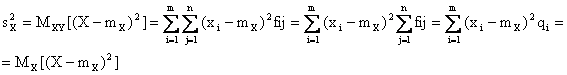
Piu' in generale posso pensare di applicare l'operatore media, a vettori o matrici le cui componenti siano funzioni di (X,Y).
Ad esempio la media della variabile doppia (X,Y), puo' pensarsi come l'operatore media applicato al vettore di componenti X e Y, che si calcola applicando l'operatore media alle singole componenti:
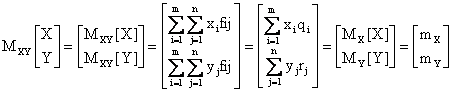 .
.
Per variabili statistiche doppie, si calcola la varianza delle singole componenti, la cui espressione, con lo stesso ragionamento fatto per le medie, e' data da:
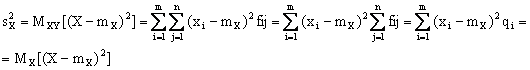

Per le varianze valgono le stesse proprieta' gia' enunciate nel caso di variabili monodimensionali.
Inoltre si calcola un ulteriore indice detto di covarianza che e' pari a
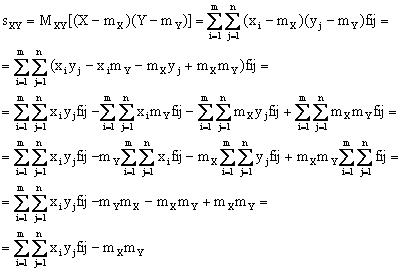 .
.
Tale coefficiente sara' prossimo a zero nel caso in cui le componenti della variabile statistica siano pressoche' indipendenti.
Gli indici di varianza covarianza di una variabile a due dimensioni (X,Y) si ordinano in una matrice 2 2, nel modo seguente:
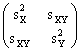 .
.
Tale matrice si ottiene applicando l'operatore media alla seguente matrice:
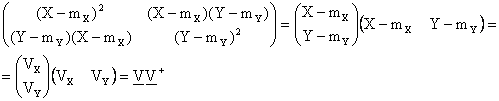
ovvero applicando l'operatore media a ciascun elemento della matrice:
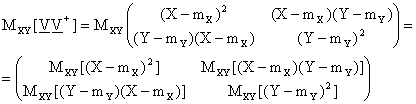
Come nel caso monodimensionale, anche nel caso bi-dimensionale e' possibile ricavare la distribuzione di una variabile statistica che sia funzione della variabile (X,Y), senza dover ricensire la popolazione. In particolare, vediamo il caso in cui la variabile (X,Y) si trasforma in una variabile mono-dimensionale:
Z=g(X,Y)
e quello in cui la variabile (X,Y) si trasformi nella variabile doppia (V,W):
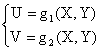
In entrambi i casi, il primo passo consistera' nel calcolare i valori argomentali assunti dalla nuova variabile. Nel primo caso per ciascuna coppia (xi,yj) si ricavera' un solo valore zi=g(xi,yj) , nel secondo caso per ciascuna coppia (xi,yj) si otterra' una coppia di valori ui=g1(xi,yj) e vj= g2(xi,yj).
A ciascun valore argomentale ottenuto (zi, ovvero la coppia (ui,vj)) si attribuira' la stessa frequenza della coppia (xi,yj) da cui deriva. Quindi si riordineranno i valori argomentali, riportando una sola volta quelli ripetuti, attribuendo loro una frequenza pari alla somma delle singole ripetizioni.
Consideriamo, ad esempio, la variabile (X,Y) in tabella
|
x\y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sia Z=XY
Si ottengono i seguenti valori argomentali:
|
x\y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
La frequenza di ciascun valore argomentale in tabella e' la stessa della coppia (xi,yj) da cui deriva: lo 0 in posizione (1,1) avra' frequenza 0,2, quello in posizione (1,2) avra' frequenza 0,1 e cosi' via.
I valori ottenuti vanno infine riordinati e in corrispondenza valutata la frequenza di ciascuno di essi:
|
z |
|
|
|
|
|
|
|
f' |
f11+f12+f13 |
f21 |
f22+f31 |
f23 |
f32 |
f33 |
|
|
|
|
|
|
|
|
Sia ora U=X2 e V=XY si ottiene
|
x\y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E riordinando
|
u\v |
|
|
|
|
|
|
|
|
f11+f12+f13=0.45 |
|
|
|
|
|
|
|
|
f21=0.15 |
f22=0.05 |
f23 =0.10 |
|
|
|
|
|
|
f31=0.10 |
|
f32 =0.05 |
f33 =0.10 |
E' facile dimostrare che anche nel caso di
trasformazioni del tipo Z=g(X,Y) e 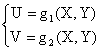 , vale il teorema della media, ovverosia che
, vale il teorema della media, ovverosia che
MZ[Z]=MXY[g(X,Y)] nel caso Z=g(X,Y)
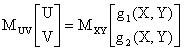 nel caso
nel caso 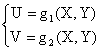 .
.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025