Le variabili casuali n-dimensionali

tecnica

Lezione #11

Le variabili casuali n-dimensionali

Consideriamo un esperimento aleatorio che dia luogo a ennuple di risultati, ad esempio il lancio contemporaneo di n dadi. La variabile casuale X mette in corrispondenza lo spazio dei possibili risultati con lo spazio Rⁿ=R R R (il prodotto cartesiano di R con se stesso n volte).

Se n=2 i risultati corrisponderanno a punti del piano cartesiano, per n=3 a punti dello spazio cartesiano.

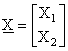 in R² e i singoli risultati dell'esperimento saranno i vettori a due componenti .

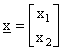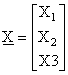 in R³ e i singoli risultati dell'esperimento saranno i vettori a tre componenti .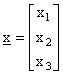

Nel caso di variabile discreta e finita in R², per ogni punto del piano, ovvero per ogni possibile risultato è data una probabilità congiunta della coppia:

che in R³ diventa:

e in Rⁿ

Ciascuna delle componenti delle variabili a più dimensioni é a sua volta una variabile casuale monodimensionale caratterizzata dalla distribuzione di probabilità marginale.

In R² le due componenti sono due variabili monodimensionali le cui rispettive distribuzioni marginali, sono:

marginale di X₁ e marginale di X₂

In R³

marginale di X₁ , marginale di X₂ e la marginale di X₃ .

In Rⁿ

marginale di X₁ , marginale di X₂ e la marginale di X_n .

Si possono calcolare, per n maggiore di due, le distribuzioni marginali di coppie di componenti. Fissata una coppia di componenti, la marginale di tale coppia si ottiene sommando la congiunta sugli indici delle componenti rimanenti.

Ad esempio in R³, si possono ricavare le tre distribuzioni delle coppie di componenti seguenti:

L'operatore media diviene:

In R²

in R³

in Rⁿ

La media sarà dunque

In R²

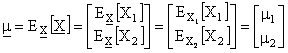
in cui la ciascuna delle componenti può essere calcolata a partire dalla distribuzione della marginale della componente corrispondente.

in R³

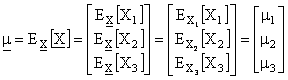
in Rⁿ

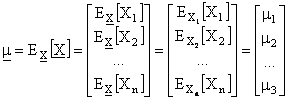
La matrice di covarianza richiede l'uso delle distribuzioni marginali delle singole componenti e delle coppie di componenti.

In R²

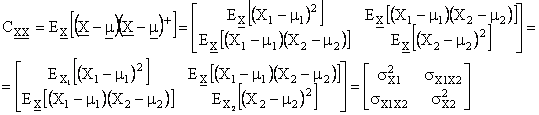
In R³

 In Rⁿ

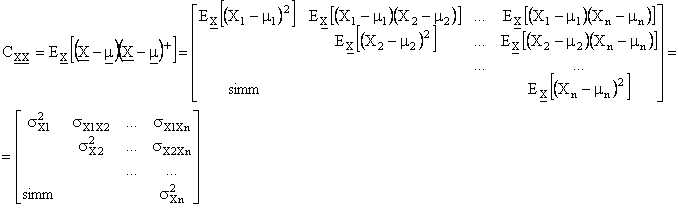
Se le componenti di una variabile a n dimensioni sono tutte indipendenti tra loro, la congiunta si spacca nel prodotto delle distribuzioni di probabilità marginali e le covarianze divengono tutte negative.

Vale inoltre il teorema della media.

da cui discendono le formule di propagazione della media e della covarianza

nel caso lineare

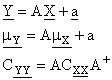
nel caso non lineare, in forma approssimata si ha

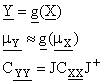
dove J eè la matrice iacobiana della trasformazione, calcolata in corrispondenza della media di X.