MECCANICA RAZIONALE - ELABORATO DI GEOMETRIA DELLE MASSE

DI

GEOMETRIA DELLE MASSE

Descrizione del sistema di lavor 232f56c o:

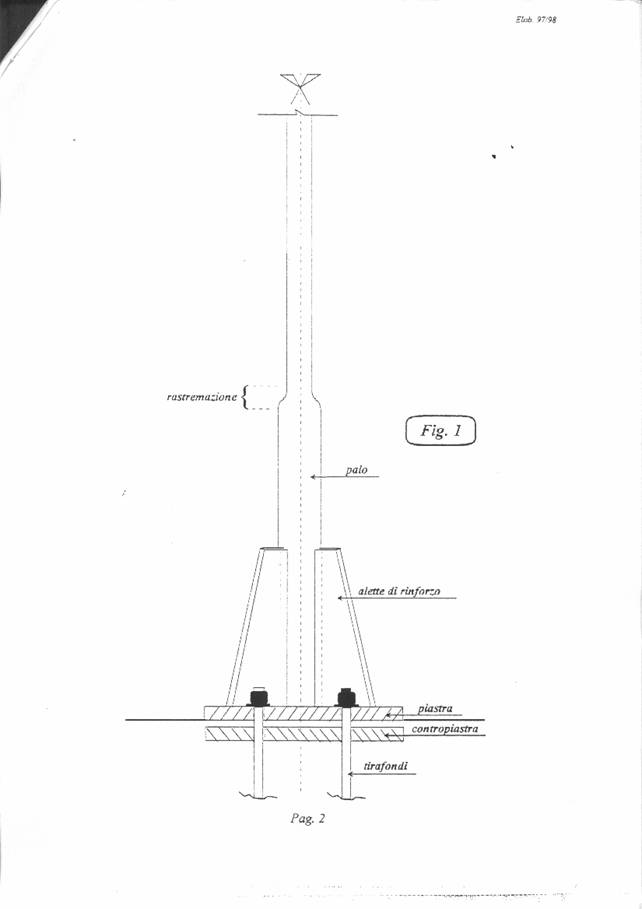
In figura 1 è stato rappresentato, in forma schematica, un palo tubolare a sezione circolare portafari rastremato in corrispondenza della zona indicata in figura e rafforzata alla base da n. 3 alette disposte in pianta in modo polar-simmetrico e saldate al palo ed alla piastra di base. Il tutto, poi, è opportunamente bullonato, mediante contropiastra e tirafondi, alla fondazione sottostante.

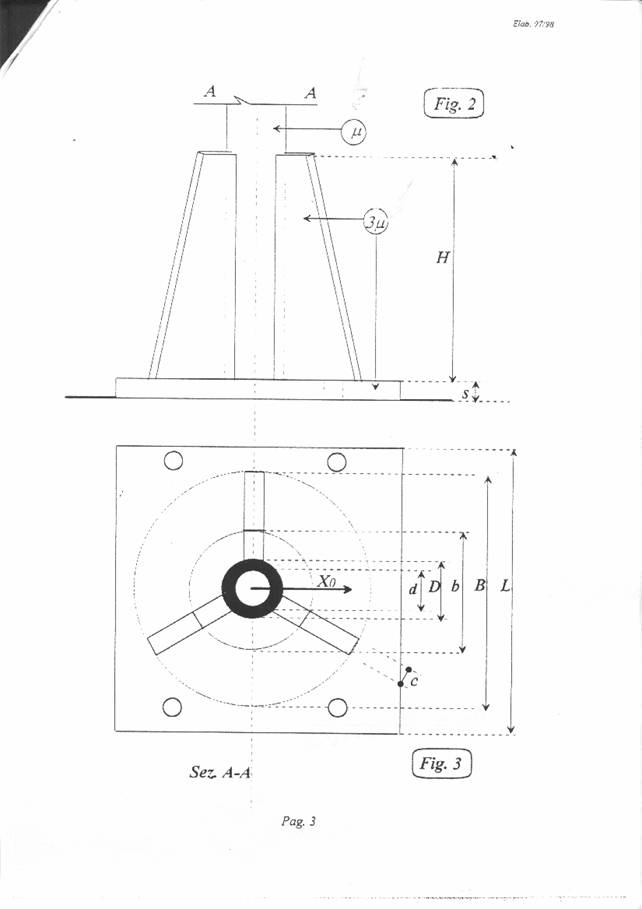
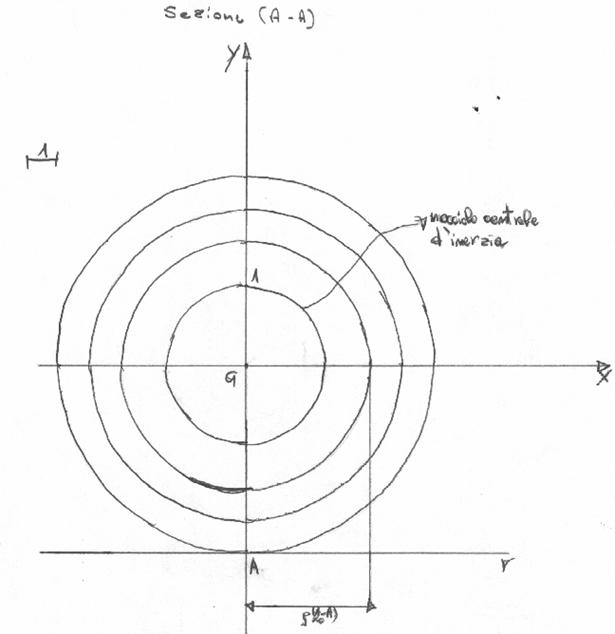
In figura 2 e 3 sono state rappresentate, rispettivamente, la vista laterale della zona rinforzata (con la piastra di base) e la sezione del palo eseguita in una zona (A-A di figura) non rinforzata.

Il materiale costituente le alette di rinforzo è la stesso di quello costituente la piastra di base ma diverso da quello del palo. Di tale differenza se ne è tenuto conto in seguito mediante l'assegnazione di differenti valori della "densità (di resistenza) m

Il sistema di rinforzo con alette qui proposto è stato realizzato per conferire alle sezioni maggiormente sollecitate del "sistema palo" (quelle cioè poste più vicino alla sezione di incastro alla piastra e al suolo) una maggiore resistenza alle sollecitazioni su di essa agenti. Tale maggiore resistenza, a sua volta, è stata ottenuta accrescendo il momento di inerzia della "sezione che resiste".

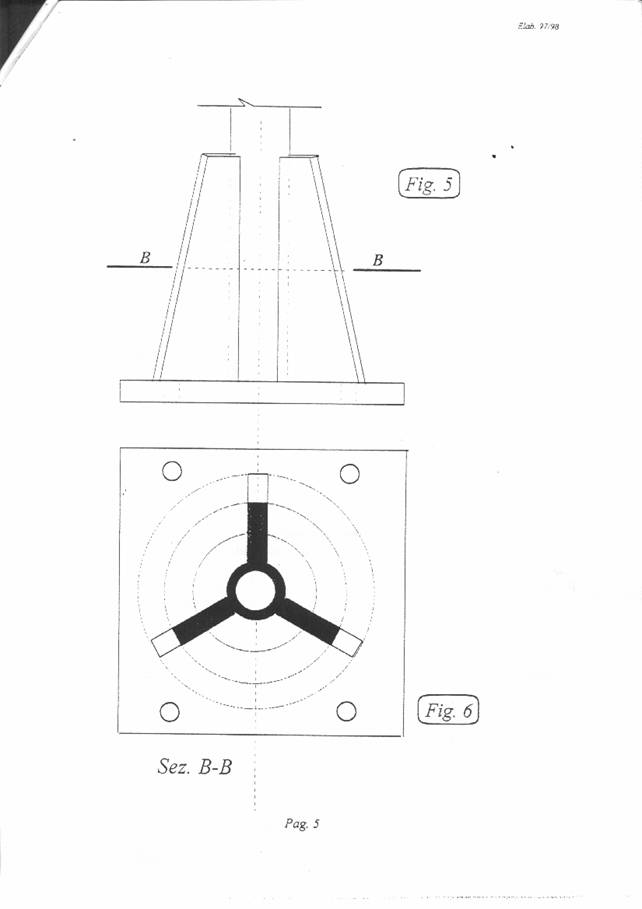
In figura 6 è stata tratteggiata la parte resistente della generica sezione (B-B) della porzione rinforzata del palo.

Definizione del problema:

Del sistema descritto si richiede di:

Determinare il valore dello spessore "c" delle ali in modo che il momento di inerzia della sezione di attacco alla piastra (sezione C-C) rispetto all'asse baricentrale X₀ (vedi fig. 3) risulti (K+10) volte quello della sezione tubolare non rastremata (sezione A-A di fig. 4) rispetto, anch'essa, ad un proprio asse baricentrale. (K è un numero il cui valore è descritto in seguito).

Per tale valore dello spessore determinare la legge di variazione del momento d'inerzia della sezione resistente del palo, rispetto ad un proprio asse baricentrale, al variare della altezza, a partire dalla sezione di contatto piastra-contropiastra. Diagrammare tale legge.

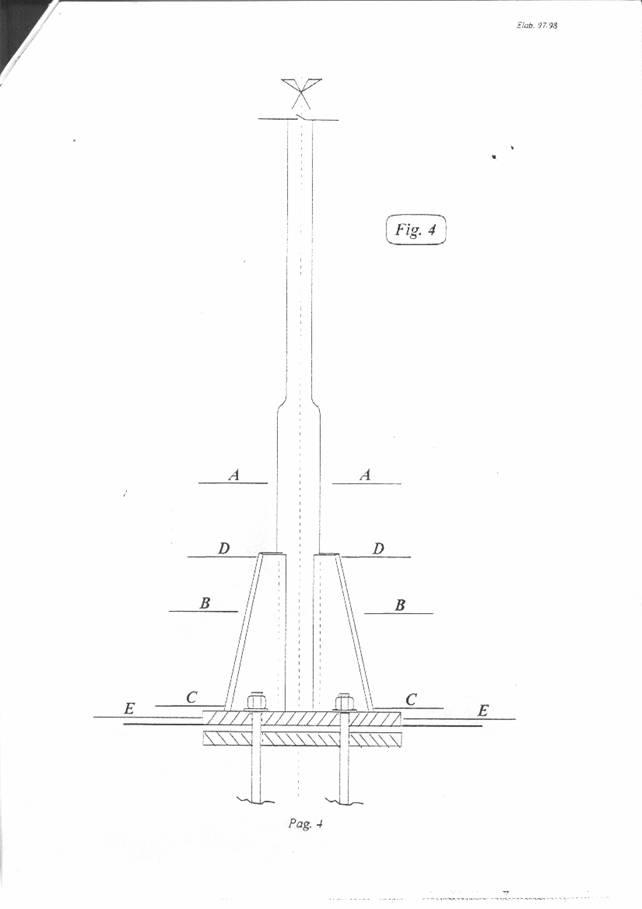
Disegnare (in scala) le ellissi centrali d'inerzia ed i relativi noccioli centrali d'inerzia delle sezioni resistenti (fig. 4):

Piastra (quadrata);

C-C di attacco alla piastra;

D-D estrema dell'ala;

A-A del palo non rastremato.

Espressione dei dati numerici: K=13

d=10,4 D=13 b=19,5 B=58,5

L=73,125    H=78 s=5 m

Determinare il valore dello spessore "c" delle ali in modo che il momento d'inerzia della sezione di attacco alla piastra, sezione C-C, rispetto all'asse baricentrale X₀ risulti (K+10) volte quello della sezione tubolare non rastremata, sezione A-A, rispetto anch'essa ad un proprio asse baricentrale.

Inizio con il calcolare il momento di inerzia della sezione tubolare senza rinforzi rispetto ad un suo asse baricentrale:

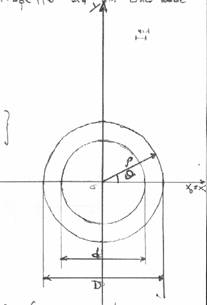
In coordinate polari:

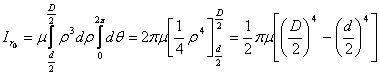
Oss.

r₀ è una retta normale al piano contenente la figura e passante per G, se considero una retta baricentrale appartenente a tale piano avrò la relazione:

,

quindi:

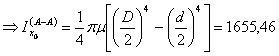
Calcolo inoltre la massa che mi sarà utile per il calcolo del raggio d'inerzia, :

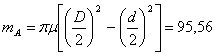
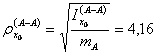
7Pertanto il momento d'inerzia della sezione d'attacco alla piastra dovrà valere:

Determino ora il momento d'inerzia della piastra quadrata rispetto ad un suo asse baricentrale:

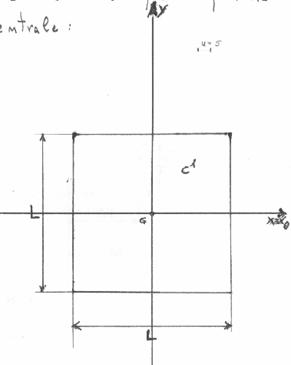
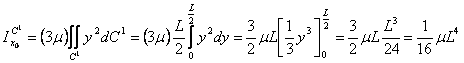
poiché:

 

completo con il calcolo della massa e del raggio d'inerzia:

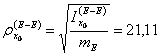
Determino ora il momento d'inerzia della sezione tubolare con rinforzi:

Oss.

decido di schematizzare con una retta la variazione della profondità delle ali (x) al variare

dell'altezza (z) ; considero la base della piastra.

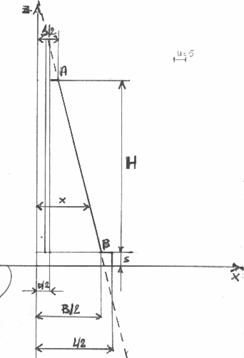
Equazione retta AB

I dati sono:

 

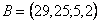
Applicando la ben nota formula per l'equazione

di una retta passante per due punti ottengo:

   

Calcolo ora il momento d'inerzia della sezione B ad una generica quota z:

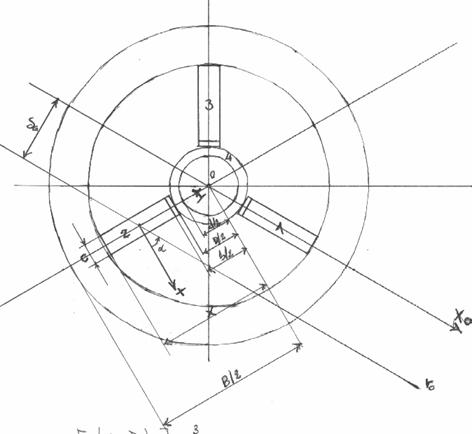
  ,calcolato in precedenza.

Ora poiché:

 

Oss.

, inoltre poiché sto considerando un riferimento centrale d'inerzia.

Applico Huygens

determino e :

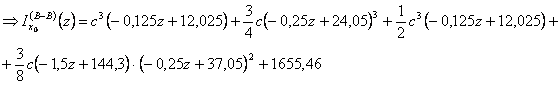
svolgendo i calcoli e semplificando i termini simili arrivo ad una scrittura di questo tipo:

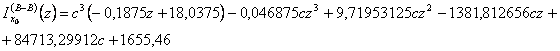
poiché deve essere:

 

Ricavo il valore di c dall'equazione di terzo grado ottenuta proprio imponendo la

Per questo valore di c studio la legge di variazione del momento d'inerzia al variare dell'altezza z :

Oss. Dal grafico si deducono diverse cose importanti:

Il momento d'inerzia nel tratto iniziale relativo allo spessore della piastra quadrata è costante, subisce poi una brusca diminuzione dovuta appunto alla brusca variazione di sezione quando si giunge nel tratto tubolare con rinforzi; da qui il momento d'inerzia diminuisce con continuità per la riduzione della parte che resiste (le alette di rinforzo), infine diminuisce ancora bruscamente per via del passaggio di sezione della zona estrema delle alette alla sezione tubolare senza rinforzi.

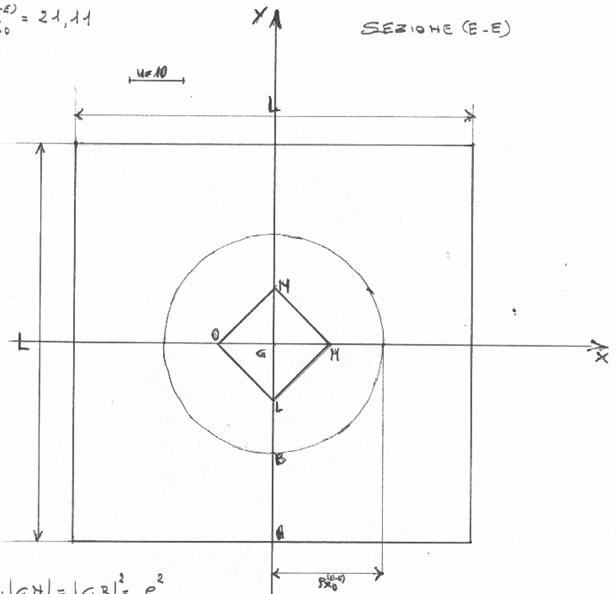
Disegno le ellissi centrali d'inerzia ed i relativi noccioli centrali d'inerzia delle seguenti sezioni resistenti:

piastra quadrata (E-E)

dati numerici utili:

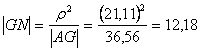
sezione d'attacco alla piastra (C-C)

dati:

poiché:

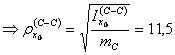
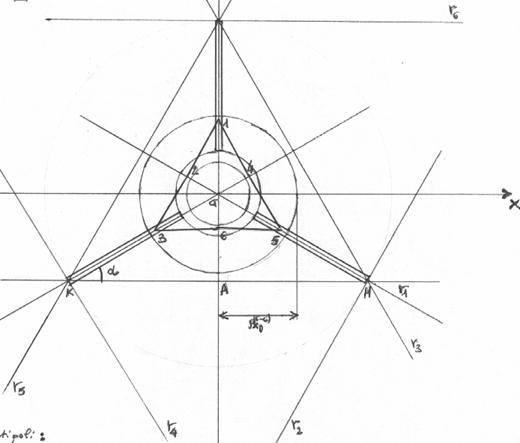
Antipoli

antipolo di

  

antipolo di

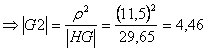
analogamente per le altre rette ottengo i punti 3,4,5,6 .

sezione palo non rastremato (A-A)

dati:

Antipoli

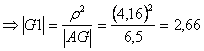
sezione estrema dell'ala (D-D)

dati:

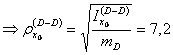
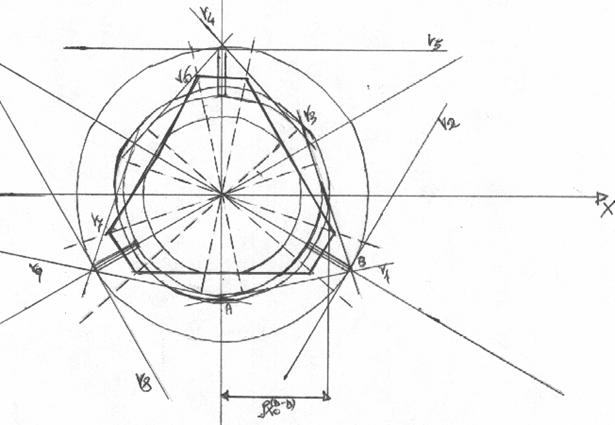
Antipoli

antipolo di

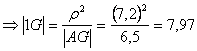
antipolo di

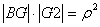
analogamente rispetto alle altre rette ricavo i punti 3,4,5,6,7,8,9 .