IMPEDENZE MECCANICHE ED ACUSTICHE

Diaframmi vibranti (membrane e piastre)

I vincoli impongono un numero discreto di modi di vibrazione, ciascuno dei quali risuona (=la Z è minima) ad una certa frequenza. Fissati i vincoli, le autofrequenze stanno in rapporti determinati con la fondamentale. Per una membrana circolare incastrata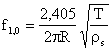

La forma conica, a parità di diametro è più rigida di quella piana ed inoltre le autofrequenze dei modi simmetrici sono molto più elevate (anche quelle dei modi simmetrici lo sono, ma molto di meno e poi comunque questi ultimi vengono impediti dal cestello dell'altoparlante).

massa e velocità equivalenti di un diaframma, per i modi simmetrici. Servono per utilizzare l'analogia elettromeccanica 1) massa e velocità centrali (il centro è dove viene applicata la forza ed ha velocità U_c): sono tali che . Si pone M_c=bM. 2) massa e velocità media : sono legate alle costanti centrali da U_m=aU_c

Schema elettrico equivalente di un diaframma. E' un circuito risonante serie con inertanza M e frequenza di risonanza . Da questa si ricava C_m. Infine conoscendo (sperimentalmente[1]) il fattore di merito si può calcolare la resistenza meccanica.

impedenze acustiche (ac.3.3-3.3.5) analogia elettroacustica (pressione-tensione, portata acustica-corrente)

Cavità di dimensioni<<l quindi pressione uniforme nel tempo nella cavità

Sotto questa ipotesi l'analogia elettroacustica discende dal fatto che una cavità chiusa si comporta come una conduttanza (cedevolezza acustica C_a=V₀/gP₀) rispetto alla pressione agente sulla parete mobile ed alla portata acustica relativa ad essa, ed invece un tubo aperto si comporta come una induttanza (inertanza acustica M_a=rl/S)

Impedenza acustica Z_a=P/y

Risonatore acustico serie e parallelo

Non idealità acustiche:

viscosità dinamica del fluido: 1) velocità non uniforme del fluido (nulla sulle pareti) quindi M_a=c_s rl/S con c_s>1. 2) resistenza acustica (dissipazione di energia elastica proporzionale alla velocità di vibrazione del fluido) in serie con l'inertanza: Z_a=R_a+jwM_a. Se la sezione diventa molto piccola R_a prevale su M_a. Ciò si ha quando

conduzione termica 1) La trasformazione non è completamente adiabatica e quindi C_a=c_pV₀/gP₀.  2) conduttanza acustica (dissipazione di energia elastica in calore) in parallelo alla cedevolezza Y_a = 1/Z_a =G_a+jwC_a

In entrambi i casi le perdite si riflettono nel fattore di merito ,

Conduzione termica in cavità cilindriche di piccola altezza

Costanti acustiche di tubi di lunghezza qualunque

impedenza specifica (ac.3.3.6) rapporto tra due grandezze locali

Z_s = P/U

Equivalenza tra le varie impedenze Z_m = Z_sS = Z_aS²

Calcolo per campi di onde piane e sferiche, impedenza caratteristica del mezzo

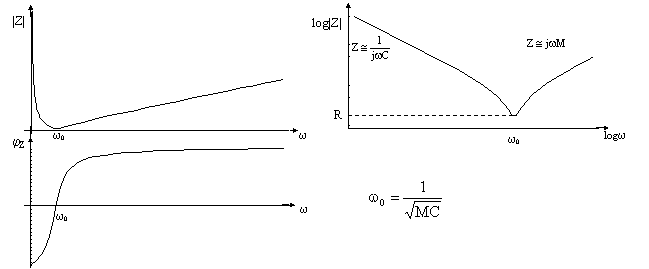
andamento in frequenza di una impedenza (elet.ac.1.2) Riportando su un grafico l'andamento di un'impedenza generica  si ottiene:

impedenza di radiazione (elet.ac.1.6) Impedenza calcolata sulla superficie dell'organo vibrante che genera le onde acustiche

Onde piane: Z_sr=r c, onde sferiche:  (casi limite 2pR₀<<l e 2pR₀>>l), disco rigido oscillante in uno schermo piano infinito:

---