 |  | |
|
| | |
|
| |
BUCA SEMI-INFINITA
Consideriamo gli stati stazionari di una particella che si muove lungo l'asse x soggetta all'azione di un campo di forza U(x) che si schematizza come segue.
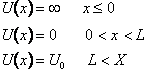343d37d 343d37d 343d37d 343d37d
Nella realtà la forza varierà con continuità. Una una particella che si muove in tale campo di forza oscillerà, secondo la meccanica classica, all'interno della buca se la sua energia è minore di U0 . Ci sono due aspetti interessanti in questo semplice problema.
a) in quali condizioni si possono realizzare stati stazionari quantistici con energia minore di U0 . Si può infatti prevedere che,al contrario di quanto prevede la fisica classica, non sia sempre possibile "localizzare " una particella nella buca. In uno stato localizzato infatti l'ampiezza della buca rappresenta una stima della incertezza con cui è nota la posizione della particella e l'energia dello stato è proporzionale alla incertezza sulla quantità di moto. Per il principio di indeterminazione al diminuire dell'ampiezza aumenta l'energia ed esiste pertanto una ampiezza minima al di sopra della quale lo stato non è più localizzato.
b) Agli stati localizzati è associata una funzione d'onda che si estende all'interno della regione considerata "proibita" dalla fisica classica. Si tratta di un primo esempio di effetto "tunnel" dell'effetto cioè per cui è possibile osservare una particella in regioni dello spazio classicamente proibite perchè l'energia potenziale supera l'energia della particella.
Il calcolo degli stati stazionari si esegue risolvendo l'Equazione di Scrodinger indipendente dal tempo separatamente nelle tre regioni in cui l'energia potenziale è costante e raccordando poi le tre soluzioni.
343d37d 343d37d 343d37d
Le soluzioni sono le seguenti rispettivamente la prima all'interno del segmento e la seconda all'esterno.
343d37d 343d37d (3)
Trattandosi di equazioni differenziali del secondo ordine le soluzioni dovrebbero contenere due costanti arbitrarie. Nella prima soluzione una costante è stata determinata imponendo la condizione al contorno in x=0 nella seconda imponendo che la soluzione tenda a zero per x che tende all'infinito. Dal reccordo delle soluzioni e delle loro derivate in x=l otteniamo
343d37d 343d37d 343d37d 343d37d (4)
Si tratta di due Eqs omogenee nelle incognite A,B.
Per avere soluzioni non identicamente nulle occorre che il determinante dei coefficienti sia nullo. Da quest condizione o più direttamente dividendo membro a membro le due Eqs. otteniamo
343d37d 343d37d 343d37d 343d37d 343d37d (5)
Si tratta di una equazione trascendente nell'Energia.
Trasformando in seno o in coseno con le note formule trigonometriche otteniamo:
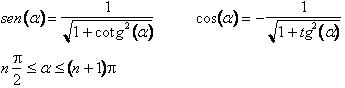343d37d 343d37d (6)
si ottiene
343d37d 343d37d 343d37d 343d37d 343d37d (7)
Per una soluzione grafica conviene introdurre un parametro m ed una variabile adimensionale x.
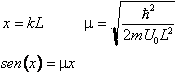343d37d 343d37d 343d37d 343d37d (8)
Ci si rende conto facilmente che esistono intersezioni tra la curva del seno e la retta di inclinazione m solo se m<1 in accordo con la stima basata sul principio di indeterminazione. All'aumentare di m aumentano le intersezioni fino a diventare un numero infinito poste in x=np per U0 che tende a zero. In tale limite si riottengono cioè gli autovalori della buca infinita.
343d37d Figura
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024
