armature

dielettrico (materiale isolante)

Quando si collega il condensatore ad un generatore di corrente continua, l'armatura collegata al polo positivo si caricherà positivamente, mentre quella collegata al polo negativo si caricherà negativamente. La quantità di elettricità dislo 111h77b cata su ciascuna armatura dipende oltre che dalle caratteristiche del sistema, anche dal valore della f.e.m. del generatore, poiché da questa dipende il numero di elettroni in eccesso che un generatore riesce a mantenere sul suo polo negativo. Nel nostro caso, più precisamente si può affermare che il numero di elettroni in eccesso sull'armatura negativa dipende dal valore della d.d.p. che tale armatura ha rispetto a quella positiva. Risulta quindi che la quantità di elettricità Q dislocata su una armatura è direttamente proporzionale alla d.d.p. V esistente fra le due armature. Si può perciò scrivere, detto C il fattore di proporzionalità, che:

Q = CV

Alla costante C è stato dato il nome di capacità elettrica. Per un dato condensatore la capacità rappresenta perciò la quantità di elettricità che esso può immagazzinare quando fra le sue armature la d.d.p. è uguale ad 1V. Infatti, per la relazione precedente, la capacità C viene definita come:

C = Q/V

COME VARIA LA CAPACITA' DI UN CONDENSATORE PIANO VARIANDO LA DISTANZA FRA LE ARMATURE.

L'esperienza mette facilmente in rilievo che la capacità di un dato condensatore aumenta avvicinando fra loro le sue armature e viceversa diminuisce se le armature vengono allontanate. Si supponga di disporre di un condensatore costituito da due armature piane, la cui distanza possa (mediante opportuno dispositivo) essere variata.

Dopo aver derivato fra le armature un elettrometro, si carichi il condensatore mediante un'opportuna batteria di accumulatori o di pile, ad una tensione per esempio di 100 volt (vedi figura).

Aprendo l'interruttore t il condensatore rimane carico e l'elettrometro segna ancora, come sappiamo, la stessa tensione di 100 volt. Se, a interruttore aperto, mediante un manico isolante, si allontana una armatura dall'altra fino a che la distanza diventi doppia, tripla, ecc. si vedrà che la tensione indicata dall'elettrometro sale rispettivamente a 200, 300 volt ecc. (vedi figura).

Se invece la distanza fra le armature viene ridotta a metà, anche la tensione indicata dall'elettrometro si riduce a metà (vedi figura).

Ciò significa che, raddoppiando la distanza fra le armature, si riduce a metà la capacità del condensatore: mentre infatti la carica elettrica dislocata sulle armature rimane sempre la stessa, la tensione invece si è raddoppiata. L'esperienza prova inoltre che se si varia la distanza fra le armature finchè permane il collegamento con il generatore (interruttore chiuso) allora la tensione indicata dall'elettrometro non varia. In tal caso infatti la tensione fra le armature rimane sempre uguale a quella fornita dalla batteria; e pertanto al variare della capacità del condensatore col variare della distanza fra le sue armature, varia la carica Q che si distribuisce sulle armature. Aumentando la distanza, la capacità diminuisce e corrispondentemente si verifica una retrocessione di cariche elettriche dalle armature lungo il circuito del generatore; avvicinando invece le armature la capacità aumenta ed il generatore disloca sulle armature delle nuove cariche elettriche in modo che resti sempre soddisfatta la relazione Q=CV.

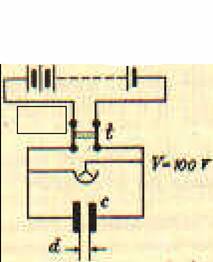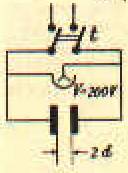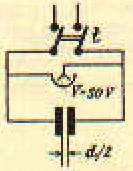CAPACITA' DI UN CONDENSATORE PIANO A VUOTO.

La figura seguente mostra una disposizione detta condensatore piano, consistente in due piatti conduttori paralleli di area A separati da una distanza d:

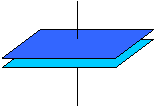
Vogliamo ora calcolare la capacità di un condensatore piano (avente come dielettrico il vuoto) una volta nota la sua geometria. Il procedimento da seguire è il seguente:

si assume che ci sia una carica Q sulle armature;

si calcola il campo elettrico E tra le due armature in funzione della carica Q, utilizzando la legge di Gauss;

conoscendo il campo elettrico, si calcola la differenza di potenziale V tra le armature mediante l'equazione:

V_f - V_i =   -

si calcola C dall'equazione:

Q = CV

Il campo elettrico tra le armature è legato alla carica Q su una armatura dalla legge di Gauss, ossia

e = q

dove q è la carica contenuta entro la superficie gaussiana e l'integrale è esteso a tutta la superficie.

Per arrivare facilmente ai risultati, è necessario ipotizzare che le linee di forza entro lo spazio compreso tra le armature siano rettilinee ed uniformemente distribuite, e ciò anche in vicinanza dei bordi. Nessuna linea esce fuori dal condensatore. A tal proposito si precisa che l'effetto di incurvatura e la fuoriuscita delle linee di forza in prossimità dei bordi sono in realtà tanto più trascurabili quanto più piccola è la distanza tra le due armature in confronto con le dimensioni trasversali delle armature stesse. I risultati cui si perverrà saranno perciò tanto più vicini alla realtà quanto più l'effetto ai bordi sarà trascurabile.

In tali ipotesi il teorema di Gauss diviene:

q = e EA

in cui A è l'area di quella parte di superficie gaussiana attraverso cui vi è effettivamente un flusso. Per questioni di comodità la superficie gaussiana viene tracciata in modo che essa racchiuda completamente la carica del piatto positivo:

A armatura carica +Q

superficie gaussiana

armatura carica -Q

Applicando quindi il teorema di Gauss con le ipotesi restrittive appena descritte si ottiene che

Q = e EA

La differenza di potenziale tra i piatti è legata al campo elettrico dall'equazione:

V_f - V_i = -

In cui l'integrale è calcolato su un qualunque percorso che va da un'armatura all'altra. Per semplicità scegliamo un percorso che segue una linea di campo dall'armatura positiva a quella negativa. In tali ipotesi i vettori sono paralleli e concordi, per cui il loro prodotto scalare è semplicemente la quantità positiva data dal prodotto dei due moduli Eds. Se ne deduce che V_f - V_i sarà sempre negativa.

Trattando di condensatori, si usa attribuire implicitamente il valore zero del potenziale ad uno dei due piatti, di modo che il potenziale V dell'altro piatto viene a coincidere con la d.d.p. Scegliendo allora il potenziale dell'armatura negativa nullo (V_f = 0) si ha:

V_i = V =

dove i segni + e - indicano che il cammino di integrazione inizia sull'armatura positiva e termina su quella negativa.

Detta quindi d la distanza tra le armature del nostro condensatore piano e ricordato che il campo elettrico è costante e quindi può portarsi fuori dall'integrale, si ha:

V = =Ed

Possiamo quindi calcolare la capacità del condensatore:

Q e EA e A

C = = =

V Ed d

Questa formula permette dunque di calcolare il valore della capacità offerta da un condensatore ad armature piane e parallele separate dal vuoto, note che siano le sue caratteristiche geometriche.

CAPACITA' DI UN CONDENSATORE PIANO CON DIELETTRICO.

Si consideri un condensatore piano tra le cui armature sia stato posto un materiale isolante, omogeneo di costante dielettrica e, il quale sia tale da riempire completamente lo spazio compreso fra le armature stesse:

Q Q_p

+ -

V

-

⁺

Ai fini pratici, è molto comodo esprimere il valore della costante dielettrica e di una certa sostanza in funzione della costante dielettrica del vuoto e . In tal caso e, che ovviamente rappresenta la costante dielettrica assoluta del materiale, viene espressa nel seguente modo

e e_r e

dove e_r ha il significato di costante dielettrica relativa del materiale considerato.

In una regione completamente riempita da un dielettrico, tutte le equazioni elettrostatiche contenenti la costante dielettrica del vuoto e devono essere modificate sostituendo questa costante con la costante assoluta del mezzo e e_r e Pertanto la capacità del condensatore piano con dielettrico diventa:

e e_rA

C =

d

La capacità di un condensatore piano, avente per dielettrico un materiale omogeneo di costante dielettrica relativa e_r, assume dunque e_r volte il valore della capacità che lo stesso condensatore presenta quando il suo dielettrico è il vuoto.

Vediamo allora come mai la capacità di un condensatore aumenta all'aumentare del valore della costante dielettrica del suo dielettrico. Per spiegare questo fatto si incominci a considerare che cosa succede quando lo spazio compreso tra le due armature di un condensatore piano, inizialmente costituito dal vuoto, carico alla tensione V e portante su ciascuna armatura la carica Q₀, si riempie con un dielettrico omogeneo avente una costante dielettrica relativa >1. Ovviamente questo si polarizza come mostrato nella figura precedente; d'altronde le cariche di polarizzazione che affiorano sulle due facce esterne del materiale, indicate con Q_p, sono di segno opposto a quelle Q₀ presenti inizialmente sulle armature, per cui la carica risultante nell'intorno di ciascuna armatura tende a diminuire per portarsi al valore Q₀ - Q_p.

Ma ciò non può avvenire se il condensatore è collegato ad un generatore elettrico che mantiene la d.d.p. V fra le sue armature, poiché il generatore vi invierà nuove cariche elettriche, al fine di neutralizzare l'azione di quelle di polarizzazione Q_p. in definitiva dunque, effettivamente su ciascuna armatura si troverà dislocata una quantità di elettricità pari a Q₀ + Q_p, mentre nell'intorno dell'armatura si farà sentire l'azione di una carica risultante (Q₀ + Q_p) - Q_p = Q₀, cioè ancora uguale a quella che si avrebbe nel caso che il dielettrico fosse il vuoto: per questo motivo il campo elettrico non ha subito variazione di sorta e vale perciò V/d, come se ci fosse ancora il vuoto.

La capacità C in questa nuova condizione, che risulta, come sempre, per definizione dal rapporto tra la quantità di elettricità totale assorbita dal condensatore (Q = Q₀ + Q_p) e la d.d.p. V fra le sue armature, tenendo presente che Q₀/V rappresenta la capacità C₀ dello stesso condensatore avente per dielettrico l'aria o il vuoto, è espressa dalle seguenti relazioni:

Q Q₀ + Q_p Q₀ Q_p Q_p

C = = = + = C₀ +

V V V V V

da cui risulta immediatamente che C > C₀.

Ma l'espressione appena scritta serve anche a dimostrare che la capacità C è tanto più grande rispetto a quella C₀, quanto più grande risulta il termine Q_p/V, cioè quanto più elevato è il valore assunto da Q_p rispetto a V. ora ciò avviene in maniera tanto più sensibile quanto più il dielettrico è polarizzabile, cioè in ultima analisi, quanto più alto è il valore della sua costante dielettrica, come volevasi dimostrare.