Impianti di turbine a gas - Rendimento del ciclo

tecnica

Impianti di turbine a gas

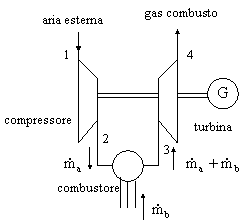
Hanno una configurazione simile a quella degli impianti di turbina a vapore, ma non sfruttano il cambiamento di fase del fluido.

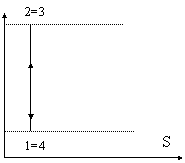
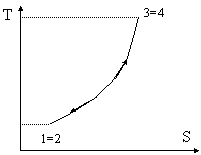
						= portata in massa dell'aria = portata in massa del combustibile Il compressore aumenta la pressione e la temperatura dell'aria; poi avviene la combustione nel combustore e i gas ad alta temperatura si espandono nella turbina; il gas combusto, in questo caso di ciclo aperto viene espulso all'esterno. Nel caso di ciclo chiuso si ha invece il raffreddamento del gas alla temp. iniziale.
					Qui a lato è raffigurato il ciclo di funzionamento ideale, in cui la massa che percorre il ciclo rimane costante, mentre in realtà è una quantità variabile. Come abbiamo detto, giunti al punto 4 si hanno due possibilità: il gas combusto viene scaricato nell'ambiente e viene sostituito con una massa d'aria a temperatura T1, oppure il gas viene raffreddato.

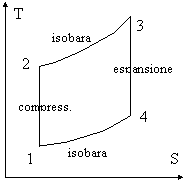
Dal punto di vista termodinamico il comportamento è il medesimo, cioè quello raffigurato nel grafico; a proposito di questo, nota che il segmento 1-2 è più piccolo del segmento 3-4 perché le isobare divergono per entropie crescenti. Questa differenza esprime il lavoro ottenuto dal gas.

Rendimento del ciclo

Calcoliamo il rendimento del ciclo in funzione del rapporto di compressione del compressore.

Gli scambi di calore avvengono solo durante le trasformazioni isobare (le altre due sono isoentropiche); il rendimento del ciclo si calcola così:

 

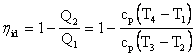
infatti Q₁ è il calore fornito a pressione costante, mentre Q₂ è il calore sottratto a pressione costante;

  

perché la trasformazione 1-2 (idem la 3-4) è una isoentropica, quindi vale la relazione:

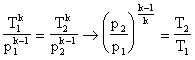
Analogamente:

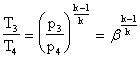    infatti p₂=p₃ e p₁=p₄;

dalle relazioni precedenti segue:

Lavoro massico ideale

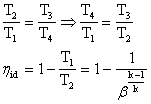
Il lavoro massico netto è pari al lavoro fornito dalla turbina meno quello speso nella compressione:

Nella trasformazione isoentropica 3-4, trascurando la variazione di energia cinetica dei gas, dall'equazione di conservazione dell'energia otteniamo:

    (convenzione macchina motrice)

Analogamente per la trasformazione 1-2:

   (convenzione macchina operatrice)

quindi

Si ottiene il lavoro massimo quando la quantità  è minima; siccome, come abbiamo visto, vale la relazione , e T₁ e T₃ sono rispettivamente la temperatura ambiente e la temperatura massima di lavoro, cioè sono valori imposti e costanti su cui non possiamo agire, la somma è minima quando T₂=T₄.

Inoltre, siccome

il lavoro è nullo in due casi:

h_id =0 , cioè b=1, e quindi T₁=T₂ e T₃=T₄

T₃=T₂

			T

Calcoliamo adesso il b_lim , cioè il valore di b quando il lavoro si annulla:

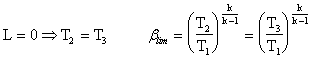
Calcoliamo adesso il b_Lmax , cioè il valore di b quando il lavoro è massimo; abbiamo già determinato che il lavoro è massimo quando T₂=T₄:

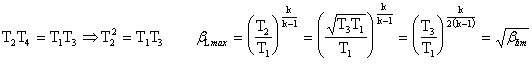
Quindi il lavoro massimo si ottiene quando

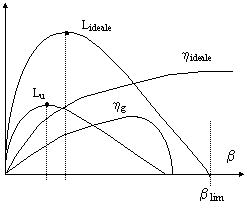
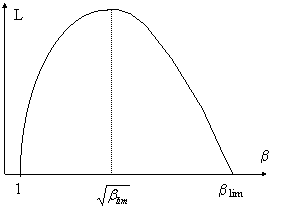
			Il grafico qui a lato riassume le considerazioni svolte finora. Per b=1 e b blim il lavoro è nullo, per il lavoro è massimo.

Dall'espressione che ci fornisce b_lim , possiamo dedurre che questo valore cresce al crescere di T₃. Inoltre possiamo calcolare la relazione esistente tra il lavoro e la temperatura massima di funzionamento T₃:

Ciclo reale

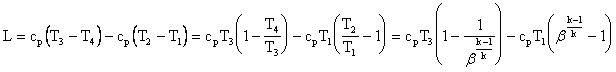
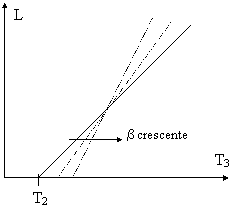
			Nel grafico, con la linea tratteggiata è stata segnato il ciclo ideale visto prima, con la linea continua è stato segnato il ciclo reale. Differenze rispetto al ciclo ideale: 1-2: non è isoentropica; inoltre il nuovo punto 2 ha una pressione maggiore del precedente; questa serve a compensare la perdita di pressione nel combustore (2-3). 3-4: non è isoentropica; inoltre la posizione del punto 4 dipende dal tipo di ciclo: aperto o chiuso.

Il lavoro del compressore è aumentato perché la pressione finale (2) è maggiore rispetto al ciclo ideale, mentre il lavoro di espansione è diminuito a causa degli attriti.

Calcoliamo dunque il lavoro totale:

Q₁= area sottesa alla trasformazione 2-3

Q₂= area sottesa alla trasformazione 4-1

Come abbiamo visto il rendimento globale è dato da:

 e inoltre:

dove: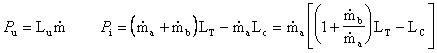   

ricordiamo che la dosatura è definita: , quindi:

			Il massimo del lavoro Lu non coincide con il massimo del rendimento globale hg, anche se i due massimi sono prossimi.

Tecniche per migliorare il rendimento

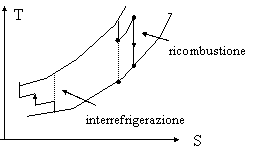
Finora abbiamo visto il ciclo "semplice"; esistono delle tecniche che rendono il ciclo più complesso, ma permettono di aumentare il rendimento fino a circa 0.35 - 0.38.

compressione interrefrigerata

ricombustione

rigenerazione

rigenerazione più compressione interrefrigerante

rigenerazione più ricombustione

Con le prime due tecniche il rendimento diminuisce, ma si ottiene un aumento del lavoro massico ottenuto; con il terzo metodo aumenta solo il rendimento; infine, con le ultime due tecniche aumentano sia il rendimento che il lavoro massico.

Compressione interrefrigerante e ricombustione

Siccome il lavoro massico è dato da: L=L_T-L_c, l'idea è quella di diminuire in qualche modo il lavoro svolto dal compressore; questo lo si può ottenere mediante refrigerazione del gas durante la compressione; d'altro canto possiamo incrementare il lavoro ottenuto dalla turbina mediante ricombustione dei gas durante la fase di espansione.

			Nel primo caso il rendimento diminuisce perché diminuisce Q2, nel secondo caso perché aumenta Q1.

Rigenerazione

Con la rigenerazione si recuperano i gas combusti e si immettono nuovamente nel combustore insieme all'aria esterna.