|
|
| |
IL MOMENTO ANGOLARE
REGOLE DI QUANTIZZAZIONE
P 515i85f er una particella che si muove nello spazio si definisce, in meccanica classica, una grandezza fisica caratteristica detta momento angolare L:
![]()
La generalizzazione immediata alla meccanica quantistica si ottiene sostituendo alla quantità di moto il corrispondente operatore vettoriale
![]()
Si noti come le componenti della quantità di moto commutino tra di loro così come commutino le componenti del vettore posizione con le componenti non omologhe della quantità di moto.
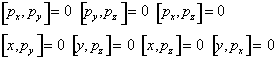
P 515i85f er le componenti omologhe si generalizza invece la regola di commutazione del moto unidimensionale.
![]()
Si noti inoltre come il momento angolare così definito sia un operatore hermitiano.
Sorge il problema della indipendena delle componenti. E' possibile misurare con precisione indipendente le componenti del momento angolare?
Calcolando i commutatori di tali componenti si ottiene
![]()
Insieme alla ( ) valgono le relazioni che si ottengono per permutazione ciclica degli argomenti x,y,z.
Dalla ( ) si deduce la relazione di indeterminazione che lega l'incertezza associata a misure di due componenti del momento angolare
![]()
Accanto alla ( ) valgono le relazioni che si ottengono per permutazione ciclica.
Il modulo quadro del momento angolare commuta peraltro con ciascuna delle componenti.
![]()
P 515i85f ossiamo pertanto scegliere come insieme rappresentativo di grandezze che caratterizzano il momento angolare il modulo quadro ed una componente . Convenzionalmente si sceglie la componente lungo l'asse z.
Un insieme completo di autofunzioni del momento angolare sarà costituito dalle autofunzioni di queste due grandezze fisiche.
![]()
Analogamente a quanto fatto per l'oscillatore armonico cerchiamo di determinare i possibili valori degli indici l,m che abbiamo associato agli autovalori sfruttando le proprietà algebriche, ovvero le regole di commutazione delle componenti del momento angolare. Anche in questo caso possiamo introdurre degli operatori di innalzamento ed abbassamento
![]()
Tali operatori si comportano rispetto ad Lz come gli analoghi operatori dell'oscillatore amonico nei confronti di H. Valgono infatti le seguenti proprietà di commutazione.
![]()
In base alle ( ) è facile mostrare che partendo da un autostato di Lz applicando l' operatore di innalzamento si ottiene un altro autostato in cui l'indice dell'autovalore è incrementato di una unità ed applicando l' operatore di abbassamento si ottiene un altro autostato in cui l'indice dell'autovalore è diminuito di una unità.
![]()
![]()
A differenza però dell'oscillatore armonico questa scala ideale presenta un limite inferiore ed uno superiore. Se si calcola infatti la norma degli stati incrementati si ottiene

Affinché tale norma sia semidefinita positiva m dovrà essere compreso tra le radici dell'equazione di secondo grado
![]()
Ripetendo lo stesso ragionamento per lo stato incrementato negativamente si ottiene
![]()
Le due condizioni saranno soddisfatte contemporaneamente se
![]()
Lo stato m=-l si deve sovrapporre a quello per m=l dopo un certo numero di applicazioni dell'operatore di innalzamento ciò comporta che 2l sia un numero intero ovvero che l sia o intero o semintero.
I valori seminteri si possono escludere studiando le proprietà di trasormazione dello stato sotto operazioni di rotazione come vedremo nel paragrafo successivo. Abbiamo così determinato le regole di quantizzazione del momento angolare. Riassumendo si hanno due numeri quantici l'uno l è un numero intero positivo ed è associato al modulo del momento angolare l'altro m è un numero intero che assume tutti i valori compresi tra -l ed l ed è associato alla componente del momento angolare nella direzione dell'asse z.
ROTAZIONI
Vogliamo mostrare come il momento angolare sia il generatore delle rotazioni. Consideriamo un punto sul piano x,y di coordinate (x,y,0). Se ruoto la posizione del punto di un angolo q rispetto all'asse z le sue coordinate muteranno come segue
![]()
P 515i85f er piccole rotazioni q,trascurando il secondo ordine in q otteniamo.
![]()
L'effetto di una rotazione sullo stato del sistema si rappresenta tramite l'applicazione di un operatore unitario U che poniamo in analogia con il caso delle traslazioni nella forma
![]()
Il valor medio della x e della y sullo stato ruotato si possono scrivere come valor medio sullo stato non ruotato di operatori trasformati x(q) e y(q) così definiti

Richiedendo che i vlori medi si trasformino come le coordinate sotto rotazioni e considerando piccole rotazioni si ottiene
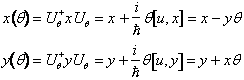
P 515i85f ossiamo identificare il generatore delle rotazioni u con Lz valendoci delle seguenti proprietà di commutazione
![]()
Lo stesso ragionamento si può ripetere per rotazioni rispetto agli assi x,y.. P 515i85f er una rotazione rispetto ad un asse qualsiasi individuato dal versore n varrà la seguente espressione dell'operatore di rotazione .
![]()
Il generatore di una rotazione rispetto ad un asse qualsiasi è coè dato dal prodotto scalare tra il versore n e l'operatore vettoriale S.
Uno stato in cui sia definito l è in generale uno stato sovrapposizione di autostati con m diverso. Se a questo stato applichiamo una rotazione rispetto all'asse z otterremo la stessa sovrapposizione in cui ogni autostato è moltiplicato per un fattore di fase associato all'autovalore corrispondente di Lz.
![]()
P 515i85f er una rotazione di 2p lo stato deve ritornare identico se le variabili posizionali sono gli unici gradi di libertà del sistema. Da tale condizione si deduce che m può assumere solo valori interi come avevamo anticipato;
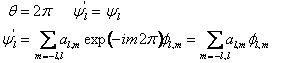
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025