Propagazione della media e della covarianza

tecnica

LEZIONE #6

Propagazione della media e della covarianza

Estendiamo le formule di propagazione al caso di trasformazion 424i85e i del tipo Z=g(X,Y), ovvero di una variabile doppia in una variabile monodimensionale e al caso di trasformazion 424i85e e tra due variabili doppie:  .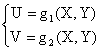

Anche in questo caso il teorema della media permette di calcolare rispettivamente, media e varianza  della Z e media e matrice di covarianza delle (U,V) senza calcolare le distribuzioni di frequenza delle variabili Z e (U,V). Se in piu' la trasformazione e' lineare, possiamo ricavare tali espressioni senza dover calcolare neanche le medie rispetto alla variabile (X,Y), tramite le formule di propagazione. Nel caso di trasformazion 424i85e i non lineari si possono ricavare formule approssimate di propagazione come gia' visto per le trasformazioni tra variabili monodimensionali.

Consideriamo dapprima la trasformazione

per il teorema della media

Se la trasformazione e' lineare

La media si calcola direttamente a partire dal vettore media della variabile (X,Y), infatti:

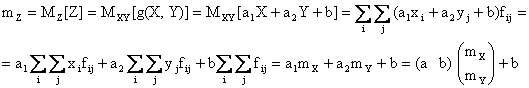
ovvero, posto

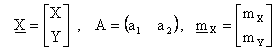
e analogamente la varianza si calcola direttamente dalla matrice di varianza-covarianza della variabile (X.Y):

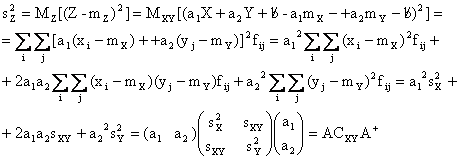
Osserviamo che tutta l'informazione che serve per calcolare la varianza della Z, a partire dalla variabile doppia (X,Y) e' contenuta nella matrice di varianza covarianza.

Nel caso in cui la trasformazione g sia non lineare, possiamo ricavare le formule approssimate di propagazione, utilizzando l'espressione linearizzata di g intorno alla media di (X,Y).

Valgono le stesse considerazioni fatte in precedenza riguardo al grado di approssimazione delle formule cosi' ricavate: essa sara' tanto migliore quanto piu' regolare e' la trasformazione g nell'intorno della media e quanto piu' e' concentrata la distribuzione di (X,Y) intorno alla media.

L'equazione linearizzata di g corrisponde a quella del piano tangente alla superficie di equazione z=g(x,y) ed e' data da

Applicando il teorema della media otteniamo:

per la media

e per la varianza

ovvero

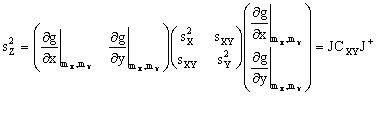
dove con J si indica la matrice iacobiana della trasformazione, qui calcolata in corrispondenza della media di (X,Y).