Fondamenti di termofluidodinamica

tecnica

Fondamenti di termofluidodinamica

Consideriamo la regione v_c delimitata dalle superifici A₁ (ingresso del fluido), A₂ (uscita) e di superficie totale A_c. Sia m(t) la massa di fluido in v_c all'istante t e sia m( 343c29d t+dt) = m(t)+dm la massa di fluido in v_c all'istante t+dt. Indicando con dm_f1 la massa che entra durante il tempo dt e con dm_f2 la massa che esce durante il tempo dt, possiamo scrivere l'equazione del bilancio della massa:

  

dividendo per dt otteniamo la stessa equazione espressa con le portate:

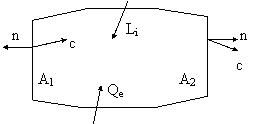
Introduciamo il versore n perpendicolare alle superficie A, e la velocità c del fluido:

  (1)

[infatti ]

Attraverso la superficie, a parte A₁ e A₂, non ci sono trasferimenti di massa, ma solo di calore Q_e e di lavoro L_i, e quindi:

   

in altre parole non c'è portata attraverso altre superfici che non siano A₁ e A₂, quindi possiamo riscrivere la (1) così:

  (2)

Nel caso di moto stazionario, cioè massa costante nel volume v_c, la (2) si semplifica:

questa espressione prende il nome di equazione di continuità: il flusso netto di massa rimane costante e quindi non ci sono accumuli di liquido. Se la densità e la velocità sono costanti su tutta la superficie possiamo scrivere: