|
|
| |
Criterio lagrangiano
La conservazione dell'energia in una trasformazione elementare è espressa da:
![]() (1)
(1)
![]() = è il calore netto
che il sistema riceve dall'esterno
= è il calore netto
che il sistema riceve dall'esterno
![]() = è il lavoro compiuto dalle forze trasmesse al sistema per contatto superficiale
con l'es 555b18f terno
= è il lavoro compiuto dalle forze trasmesse al sistema per contatto superficiale
con l'es 555b18f terno
![]() =è la variazione di energia
del sistema conseguente al calore e al lavoro ricevuti
=è la variazione di energia
del sistema conseguente al calore e al lavoro ricevuti
Nota: queste quantità sono scritte in lettere corsive; quando invece sono scritte in lettere non corsive, indicano le stesse grandezze, ma riferite all'unità di massa.
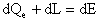 (2)
(2)
![]() = è il calore netto
che il sistema riceve dall'esterno per unità di massa:
= è il calore netto
che il sistema riceve dall'esterno per unità di massa: ![]()
![]() = è il lavoro compiuto dalle forze trasmesse al sistema per contatto superficiale
con l'es 555b18f terno per unità di massa:
= è il lavoro compiuto dalle forze trasmesse al sistema per contatto superficiale
con l'es 555b18f terno per unità di massa: ![]()
![]() =è la variazione di energia
del sistema conseguente al calore e al lavoro ricevuti per unità di
massa:
=è la variazione di energia
del sistema conseguente al calore e al lavoro ricevuti per unità di
massa: ![]()
L'energia E si può scomporre in diversi tipi di energia:
![]()
![]()
U=energia interna, U=energia interna per unità di massa
Ec=energia cinetica, Ec= energia cinetica per unità di massa
Eg=energia potenziale, Eg= energia potenziale per unità di massa
Ew energia rotazionale, Ew= energia rotazionale per unità di massa
Integrando lungo una trasformazione generica tra due stati, otteniamo:
![]()
(dQe e dL non sono differenziali)
![]()
![]() (3)
(3)
trascurando l'energia potenziale e rotazionale:
![]()
![]() (4)
(4)
Gli attriti inevitabili in ogni trasformazione danno origine alle perdite per resistenze passive, indicate con Lw o Lw. Questa quantità non compare esplicitamente nella (3) o (4).
Si può dimostrare che il bilancio dell'energia meccanica massica (cioè riferita all'unità di massa) del sistema elementare è:
![]() (5)
(5)
Sostituendo questa relazione nella (2) si ottiene:
![]() (6)
(6)
dove i
è l'entalpia del sistema: ![]()
Per una trasformazione reversibile, cioè priva di attriti, Lw=0.
Criterio euleriano
Indichiamo con
![]() la potenza termica
fornita al sistema attraverso le pareti del volume di controllo non
attraversate dal fluido
la potenza termica
fornita al sistema attraverso le pareti del volume di controllo non
attraversate dal fluido
![]() la potenza meccanica (Pi)
fornita al sistema dagli organi mobili
la potenza meccanica (Pi)
fornita al sistema dagli organi mobili
![]() la portata in massa di un fluido
la portata in massa di un fluido
Nota: sono vere le seguenti relazioni:
![]() e
e ![]() (7)
(7)
Si dimostra che il primo principio, scritto in forma euleriana, con riferimento all'unità di massa, è:
![]() (8)
(8)
Siccome i due criteri si equivalgono quando
l'intervallo di tempo considerato tende a zero, possiamo ricavare ![]() dalla (6), integrare e sostituire nella (8), ottenendo:
dalla (6), integrare e sostituire nella (8), ottenendo:
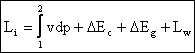 (9)
(9)
Un ciclo diretto ha lo scopo di produrre lavoro meccanico, e il suo rendimento è:
![]() (10)
(10)
dove L è il lavoro (massico) svolto nel ciclo e Q1 è la quantità di calore (massico) fornita al fluido nel ciclo.
In un ciclo, la variazione di energia DE è nulla, perché E è una funzione di stato; dal primo principio:
![]()
nota che abbiamo utilizzato la convenzione di segno dei fluidi motori, cioè dei fluidi che fanno lavoro positivo sull'esterno,
![]()
dove Q1 è il calore fornito al fluido e Q2 è il calore sottratto al fluido nel ciclo; quindi possiamo scrivere:
![]() (11)
(11)
Il lavoro massimo ottenibile da un sistema, assegnati i livelli di temperatura T1 e T2, si ottiene fornendo dall'esterno calore al sistema tutto alla temperatura massima T1, sottraendo calore al sistema tutto alla temperatura minima T2, con trasformazioni intermedie adiabatiche e senza attrito.
Postulati di Carnot: il rendimento del ciclo dipende solo da T1 e T2 il rendimento del ciclo reversibile è: Per ciclo reversibile si intende dire che
le due adiabatiche sono reversibili
La trasformazione adiabatica garantisce la
mancanza di scambio di calore nelle trasformazioni intermedie.
![]()
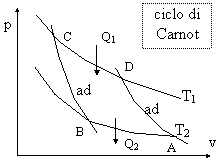
Il rendimento del ciclo reversibile è superiore a quello del ciclo irreversibile:
![]()
Si dimostra che la quantità ![]() è un differenziale esatto; in altre parole
il suo integrale definito non dipende
dagli estremi di integrazione. Quindi, integrando questa quantità su due
trasformazioni termodinamiche differenti ma con identici estremi, si ottiene lo
stesso risultato.
è un differenziale esatto; in altre parole
il suo integrale definito non dipende
dagli estremi di integrazione. Quindi, integrando questa quantità su due
trasformazioni termodinamiche differenti ma con identici estremi, si ottiene lo
stesso risultato.
Come già accade con l'energia interna U,
funzione di stato il cui differenziale esatto è ![]() , anche qui abbiamo una funzione di stato che chiamiamo
entropia:
, anche qui abbiamo una funzione di stato che chiamiamo
entropia:
![]()
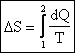 (12)
(12)
dQ tiene conto del calore scambiato netto e del calore (sempre positivo) introdotto dall'interno del fluido a causa dell'attrito:
![]()
Nel caso di trasformazione reversibile abbiamo Lw=0 e quindi:
![]() (13)
(13)
Come succede per l'energia interna U, la variazione di entropia in un ciclo reversibile è nulla:
![]()
invece in un ciclo irreversibile è negativa:
![]()
Combinando la (6) con la (12) otteniamo:
![]()
![]() (14)
(14)
Un gas perfetto soddisfa la seguente equazione di stato:
![]() (15)
(15)
dove:
p è la pressione del gas
v è il volume massico del gas
R è una costante che dipende dal tipo di gas
T è la temperatura del gas
Per un gas perfetto le capacità termiche massiche a pressione e a volume costante non dipendono né dalla pressione né dalla temperatura, e sono così definite:
![]() (16)
(16)
La capacità termica massica in una trasformazione generica è così definita (vedi la (6)):
![]()
In una trasformazione isocora la variazione di volume dv è nulla:
![]() (17)
(17)
In una trasformazione isobara la variazione di pressione dp è nulla:
![]() (18)
(18)
Nota bene: la (17) e la (18) hanno validità generale, cioè sono vere per qualunque tipo di trasformazione; infatti qualunque trasformazione può essere ricondotta a un'isoterma più un'isocora, oppure a un'isoterma più un'isobara; infatti nell'isoterma non si ha variazione di energia interna U né di entalpia i.
Possiamo dimostrare che ![]() :
:
![]()
![]()
Nota: R è una costante positiva, quindi cp > cv.
Un gas quasi perfetto è un fluido che soddisfa l'equazione di stato dei gas perfetti, ma le capacità termiche massiche dipendono dalla temperatura.
Un gas reale è viscoso e soddisfa ad un'equazione del tipo:
![]()
dove z è una funzione che dipende dal tipo di fluido e vale 1 per i gas perfetti e quasi perfetti.
Per una trasformazione generica vale la relazione:
![]()
|
trasformazione |
caratteristiche |
m |
c |
|
isobara |
p=cost |
|
cp |
|
isocora |
v=cost |
|
cv |
|
isoterma |
T=cost |
|
|
|
isoentropica |
pvk=cost |
k=cp/cv |
|
|
politropica |
pvm=cost |
altro |
costante |
isoentropica = adiabatica reversibile, quindi ![]() ,
, ![]() quindi
quindi ![]()
politropica = trasformazione con capacità termica massica costante
Per ricavare l'equazione della isoentropica si procede in questo modo:
![]() ma
ma
![]() , quindi:
, quindi:
![]()
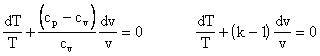
Integrando:
![]()
![]()
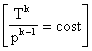
Vediamo le 4 trasformazioni sul diagramma di Clapeyron:
m=0 isobara m=1 isoterma m=k isoentropica m= isocora isoterma: è
un' iperbole equilatera: pv=cost p
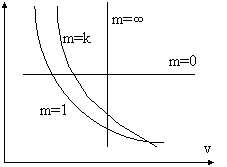
Vediamo le 4 trasformazioni sul diagramma entropico:
T isobara quindi l'isobara è un esponenziale: isocora
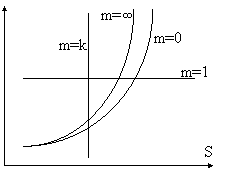
![]()
![]()
![]()
![]()
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025