Quindi in presenza di campo elettrico o magnetico il sistema si deformerà e si verrà a creare un dipolo elettrico atomico. Comunque, essendo la massa dell'elettrone molto minore di quella del protone, assumiamo che sia solo la nube elettronica a muoversi e che invece il nucleo resti fermo.

Nel caso di molecole polari, i dipoli sono già pre 919d37j senti in assenza di campo elettrico, ma la loro orientazione casuale determina un momento complessivo macroscopico nullo; la presenza del campo orienta i vari dipoli producendo un momento complessivo non nullo.

polarizzazione

Si definisce un momento di dipolo macroscopico a partire dai momenti[2] atomici (o molecolari) :

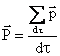con dt=elemento infinitesimo di volume

E' come se fosse una densità spaziale di momento di dipolo.

A sua volta, un dipolo atomico è in realtà la somma di tanti dipoli elettrone-nucleo. Andiamo ora a considerare l'energia potenziale U di un elettrone, relativa al campo elettrico generato dal nucleo, dagli altri atomi ed elettroni vicini e dal campo esterno; essa dipende dalla deformazione d del dipolo secondo una certa curva[3]:

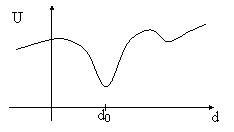Applicando un campo elettromagnetico esterno, su ogni elettrone agirà la forza di Lorentz che però sarà praticamente pari a q, perché il termine è di solito molto minore di q, essendo in modulo B=E/c.

Ora, se essa è molto minore della forza elastica che tende a far tornare l'elettrone in equilibrio, ovvero la forza coulombiana di attrazione del nucleo, legata al campo elettrico generato da quest'ultimo, allora possiamo trattarla come una perturbazione; possiamo cioè supporre che la deformazione d rimanga all'interno della buca di minimo e possiamo quindi approssimare l'andamento del potenziale come parabolico (cioè quello tipico dell'oscillatore armonico). Questo vorrà dire che applicando una forza q, l'atomo si deformerà come un oscillatore armonico con una certa costante elastica k:

kx = qE    con x = d d₀

Dunque assumerà un momento di polarizzazione:

E corrispondentemente, se il materiale ha una densità di elettroni pari a N, la polarizzazione macroscopica sarà:

Quindi per campi elettrici piccoli rispetto al campo elettrico atomico la polarizzazione è proporzionale al campo. Il campo generato dal nucleo vale circa 10¹⁰ V/m ed è molto grande.

Normalmente invece i campi elettrici esterni sono dell'ordine di 10³ V/m quindi molto minori.

Con i laser però si raggiungono valori molto più alti, tali da invalidare l'approssimazione vista ora; si parla in questo caso di ottica non lineare. Nell'ottica non lineare la polarizzazione dipende dal campo elettrico secondo una relazione non lineare del tipo:

Torniamo al caso dell'ottica lineare.

La costante di proporzionalità tra campo elettrico e polarizzazione viene indicata con:

dove c viene detta suscettività e nel vuoto vale 0. Consideriamo solo materiali con c>0, ovvero con polarizzazione concorde al campo elettrico. Si definisce poi la costante dielettrica relativa:

e_r c e e e e_r

In questo modo possiamo compattare la scrittura della prima equazione di Maxwell in presenza di dielettrici; infatti, tenendo conto delle cariche aggiuntive r_p dovute alla polarizzazione, tale equazione dovrebbe scriversi come:

Sappiamo (vedi Fisica II) che:

Quindi possiamo scrivere:

Definiamo allora un vettore ausiliario detto spostamento elettrico:

Dunque la prima equazione di Maxwell diventa:

approssimazioni

L'approssimazione che abbiamo visto, di proporzionalità tra campo elettrico e polarizzazione viene detta approssimazione di mezzo lineare. Inoltre in generale e deve essere trattato come un tensore e questo implica che la polarizzazione, pur mantenendo la proporzionalità con il campo elettrico, può non avere la stessa direzione (anisotropia). Per molti materiali però e può essere trattata come uno scalare; si parla in questi casi di mezzo isotropo.

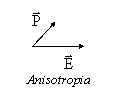Un'ulteriore semplificazione si ottiene quando e è costante nello spazio, e si parla di mezzo omogeneo.

Per un mezzo lineare, isotropo e omogeneo possiamo portare fuori dalla divergenza e nella prima equazione di Maxwell, e scrivere:

magnetizzazione

Anche per la magnetizzazione accade una cosa analoga, cioè in condizioni di linearità il vettore di magnetizzazione è proporzionale al campo magnetico attraverso una costante di suscettività magnetica c_m

Normalmente però, nello studio dell'ottica le proprietà magnetiche sono sempre trascurabili per cui non ci interessiamo della trattazione di questo caso.

equazioni di maxwell ed onde elettromagnetiche

Riportiamo le equazioni di Maxwell e a fianco la loro forma nel caso di mezzi lineari omogenei isotropi e in assenza di cariche elettriche libere e di correnti (r = 0 e J = 0):

   

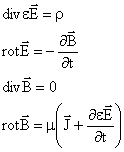
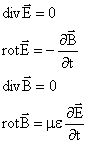
Applicando il rotore ad ambo i membri della seconda equazione ed utilizzando anche le altre equazioni, dopo alcuni passaggi si possono ricavare le equazioni delle onde elettromagnetiche:

e

Queste due equazioni vettoriali corrispondono a due sistemi di 3 equazioni scalari, che valgono, ad esempio nel caso del campo elettrico[4]:

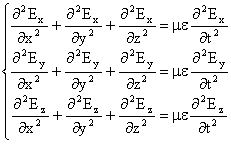
Essendo l'espressione del campo elettrico:

onde piane trasversali

Mettiamoci nel caso in cui E sia costante sul piano xy, cioè E_x E_y e E_z non dipendono da x e y:

E_x(x,y,z,t) = E_x(z,t) E_y(x,y,z,t) = E_y(z,t) E_z(x,y,z,t) = E_z(z,t)

In questo modo l'equazione vettoriale delle onde si riduce alla forma:

Questa equazione rappresenta tre equazioni scalari, che in questo caso sono indipendenti, cioè possono essere risolte separatamente; infatti in generale E_x , E_y ed E_z sono legate dalle equazioni di Maxwell[5], per esempio dalla prima:

In questo caso invece ==0 (i = x,y,z) e quindi possiamo limitarci a considerare anche una sola delle tre equazioni scalari, essendo tra loro indipendenti. Prendiamo quella lungo x:

vogliamo dimostrare che sicuramente questa equazione ammette soluzioni del tipo:

E_x(z,t) = f(z vt)

La soluzione f(z vt) descrive una funzione di una certa forma f(z) che trasla lungo l'asse z ad una velocità v che è la definizione di onda progressiva o regressiva. Se poniamo x = zvt, possiamo scrivere:

e

Derivando una seconda volta si ha:

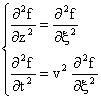
Equazione caratteristica delle onde

Dunque sicuramente un'onda di questo tipo è una soluzione possibile per le equazioni delle onde. Notiamo inoltre che essa sarà dotata di una velocità:

dunque nel vuoto dovrà essere:

Sappiamo che l'indice di rifrazione n è definito come:

Quindi potremo scrivere:

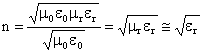
Dove abbiamo tenuto conto che nei mezzi di interesse ottico m_r è praticamente 1.

onde piane monocromatiche

Abbiamo visto quindi che una soluzione molto semplice delle equazioni delle onde è un campo elettrico costante su ogni piano parallelo al piano xy e variabile nel tempo.

La variazione nel tempo la possiamo vedere come dovuta alla traslazione lungo z di una certa forma f(z) con velocità .

E' conveniente considerare variazioni nel tempo (ovvero forme lungo z) di tipo sinusoidale poiché mediante la scomposizione in serie di Fourier qualunque funzione temporale può essere vista come una somma di sinusoidi di frequenza diversa.

Avremo quindi un campo elettrico del tipo:

E_x(z,t) = E_0xsink(z vt)  (analogamente per le altre componenti)

Il parametro k è inserito per rendere adimensionale l'argomento del seno ed ha quindi le dimensioni dell'inverso di una lunghezza ovvero le dimensioni di una frequenza spaziale. E' detto numero d'onda.

Un onda di questo tipo viene detta onda piana monocromatica trasversale polarizzata linearmente.

Se per esempio la direzione di oscillazione è una certa (si mantiene sempre nel piano xy trasversale alla propagazione), abbiamo ancora un'onda polarizzata linearmente e la possiamo vedere come la composizione di due onde oscillanti una lungo x e una lungo y:

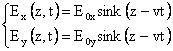   ovvero in maniera compatta

Calcoliamo il periodo di oscillazione T: in un punto z₀ all'istante t₀ l'argomento del seno vale kz₀ kvt₀ . Il periodo T sarà tale che all'istante t₀+T, sempre nel punto z₀, la differenza tra i due argomenti sarà 2p

kz₀ kv(t₀+T) kz₀+kvt₀ = 2p

Quindi frequenza e pulsazione saranno:

    w = kv

Analogamente, la lunghezza d'onda, ovvero il periodo spaziale sarà   

Possiamo allora riscrivere l'onda come:

Mettiamoci ora nel caso ancora più generale, cioè quando la direzione di propagazione non è z ma una certa . L'argomento del seno, che contiene la variabilità nello spazio e nel tempo, dovrà essere costante su ogni piano ortogonale al vettore in ogni istante.

Essendo un vettore, conviene scegliere anche k come vettore avente la stessa direzione di , cioè la direzione di propagazione, in modo tale che w rimanga scalare.

Indicando con il generico punto dello spazio (x,y,z), il piano ortogonale a è quello formato dai vettori ortogonali a e cioè formato da tutti i vettori tali che .

Questo però è il piano passante per l'origine. Tutti gli altri piani paralleli si ottengono traslando e cioè sono dati da ovvero .

Quindi se scriviamo sin, l'argomento del seno sarà costante su ogni piano diretto secondo e dunque un'onda piana monocromatica polarizzata linearmente secondo e propagantesi lungo potrà scriversi in generale come:

onde sferiche monocromatiche

Un'onda sferica ha come superficie equifase una sfera, quindi l'argomento del seno sarà . Inoltre, per mantenere l'energia per unità di superficie costante, l'ampiezza dovrà diminuire come 1/r. Otteniamo quindi:

Questa volta k è uno scalare.

intensità di un'onda piana

Nel calcolo dell'energia trasportata da un'onda piana, viene fuori il vettore di Poynting, che è definito come e nel caso di un'onda piana[6] vale . Il suo modulo è detto intensità istantanea e rappresenta l'energia che all'istante t fluisce nell'unità di tempo attraverso la superficie unitaria disposta ortogonalmente alla velocità di propagazione.

Si trova:

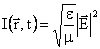
Attenzione, non è il modulo della notazione complessa ma il modulo del vettore ampiezza. Quindi ad esempio per un'onda piana si avrà, nelle due notazioni:

e

Si parla inoltre anche di intensità media, che è l'intensità istantanea mediata su un periodo di oscillazione. Si osserva che la media su un periodo del 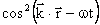è 1/2 (lo stesso per il sin²) e quindi, per un'onda piana:

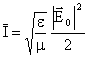  (normalmente in ottica il fattore non viene considerato)

disturbanza e altre approssimazioni

Se supponiamo come ulteriore approssimazione che le varie componenti E_x , E_y ed E_z siano indipendenti[7] (il che è vero nel caso di onda piana) e lo stesso per le componenti di B, possiamo descrivere le onde con un'unica grandezza scalare, detta disturbanza V(r,t) che genericamente rappresenta ciascuna di queste componenti.

Per la disturbanza varrà quindi l'equazione scalare delle onde:

Questa approssimazione, detta approssimazione scalare, è giustificata dal fatto che normalmente fa previsioni abbastanza in accordo con gli esperimenti.

Inoltre limitiamo il nostro interesse a soluzioni di tipo monocromatico:

V(r,t) = V(r)cos(wt+j

Normalmente per compattare le scritture e semplificare alcuni calcoli si usa il simbolismo complesso:

V = V(r) e ^iwt con V(r) = A(r) e^iF(r)

La parte reale di V è la V(r,t) vista prima.

cammino ottico

Dati due punti A e B a distanza r in un mezzo di indice di rifrazione n, si definisce cammino ottico tra i due punti:

l = nr

Essendo n=c/v, dove v è la velocità delle onde in quel mezzo, il cammino ottico risulta essere pari a:

dove t è il tempo impiegato dalla luce per spostarsi da A a B. In pratica il cammino ottico è lo spazio percorso dalla luce nel vuoto nel tempo impiegato per andare da A a B (nel mezzo n).

Consideriamo un'onda piana o sferica in due punti disposti lungo il cammino di propagazione (quindi per l'onda piana ) allo stesso istante t. L'argomento del coseno, ovvero la fase del campo, valgono in entrambi i casi (piana o sferica):

cos (kr₁ wt) e cos (kr₂ wt)

Dunque se ci spostiamo di r=r₂ r₁, l'onda si sfasa di kr, ovvero[8] k₀nr.

Quindi lo sfasamento di un'onda di frequenza w (e quindi k₀ = w/c) che percorre un tratto r in un mezzo di indice di rifrazione n è:

Dj = k₀nr = k₀l

velocità di gruppo

Consideriamo un insieme di onde piane armoniche con frequenze diverse che si propagano nella stessa direzione in un certo mezzo.

Nel caso ideale hanno tutte la stessa velocità v = c/n, ma in realtà se consideriamo la dispersione, n dipende da w e quindi anche v(w) = c/n(w

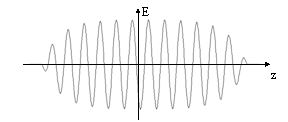Un particolare insieme di onde piane di estremo interesse pratico è il pacchetto d'onda, ovvero un treno d'onda armonico di lunghezza d'onda propria nel vuoto l e durata finita Dt (e quindi di lunghezza nel vuoto Dz = cDt). Esso può essere scomposto spazialmente secondo Fourier in tante componenti di vettore d'onda diverso (ovvero di lunghezza d'onda diversa):

(1)

Ogni componente e^i[kz-w(k)t] si muoverà nel mezzo con una certa frequenza w(k) dipendente dalla lunghezza d'onda[9].

La g(k) invece è il peso di ciascuna componente.

Poiché e allora

Vediamo come è fatta la g(k); se consideriamo un istante fissato, per esempio per semplicità t=0, possiamo schematizzare il treno d'onda come una sinusoide troncata, cioè:

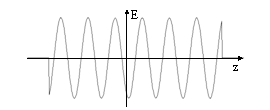
La (1) è allora l'antitrasformata di g(k) e si può vedere facilmente (vedi teoria dei segnali) che g(k) corrisponde ad una sinc.

Per k>0 si ha:

Osserviamo che la larghezza della sinc è inversamente proporzionale al suo argomento e cioè Dz, e se indichiamo con Dk la sua larghezza a metà del valore massimo si ha che .

Supponiamo allora che Dz sia abbastanza largo e quindi Dk abbastanza stretto e supponiamo che w(k) vari lentamente con k.

Possiamo allora sviluppare w(k) in serie intorno a k₀ fermandoci al primo ordine:

Riscriviamo lo sviluppo secondo Fourier per tempi t

A parte il fattore di fase fuori dall'integrale, osserviamo che ogni componente di lunghezza d'onda trasla approssimativamente con la stessa velocità . Ovviamente questa è un'approssimazione tanto più valida quanto più w(k) ha un comportamento lineare.

---