|
|
| |
Tecniche di Calcolo Economico
Quando un perito viene chiamato a formulare un giudizio di stima deve ricorrere talora alla matematica finanziaria.
L’interesse può definirsi un compenso che viene corrisposto a colui che cede ad altri l’uso di un capitale monetario per un certo periodo di tempo; quindi, detto interesse viene commisurato alla durata del prestito ed alla grandezza del capitale mutuato.
Generalmente esso viene stabilito in un tanto per cento del capitale per ogni unità di tempo di impiego ( in genere l’anno, o i sei mesi, o i tre mesi, ecc ).
- Il tasso di interesse, indicato con il simbolo “r”, può essere espresso in percentuale ( % ) o numericamente.
- L’interesse, indicato con il simbolo “i” o “I”, è dato dalla formula:
![]()
Dove:
“C0” è il capitale di partenza;
“r” è il tasso di interesse, come si è già visto sopra;
“n” è il tempo espresso in anni.
L’interesse è il prezzo che si paga per l’uso di un capitale, la sua unità è il tasso e si indica con il simbolo “r” o “i”.
L’interesse si distingue in interesse semplice e interesse composto:
si ha l’interesse semplice quando gli interessi maturati da un capitale, in un dato tempo, non maturano a loro volta alti interessi, infatti viene ca 444g68e lcolato per tutto il periodo di impiego, anche se di parecchi anni, sulla somma originariamente impiegata. In linea di massima si parla di interesse semplice se il tempo a cui si riferisce è inferiore, o al massimo uguale, ad un anno.
si ha l’interesse composto quando si maturano gli interessi degli interessi; quindi l’interesse prodotto dal capitale si aggiunge al capitale stesso alla fine di ciascuna unità di tempo di impiego e diventa a sua volta fruttifero di interessi con il capitale originario.
Interesse semplice
Montante = Capitale + Interesse
Montante unitario = q = 1 + r ← in un anno
· Esempio 1
Tizio deposita, in buoni fruttiferi presso l’Ufficio Postale, 3.000 € al tasso di interesse del 5%. Calcolare l’interesse.
Dato che si parla di interesse semplice il tempo è uguale ad un anno. Quindi:
![]() €
€
Dalla formula dell’interesse si ricavano facilmente la formula del valore scontato ( C0 ), e il tasso di interesse:
![]() ;
; ![]() ;
;
considerando, però, il tempo pari ad un anno le formula precedenti diventano:
![]() ;
; ![]() .
.
La formula ![]() , detta anche di capitalizzazione, è di
fondamentale importanza per determinare il valore di un bene suscettibile di
fornire un reddito medio annuo costante e tendente all’infinito.
, detta anche di capitalizzazione, è di
fondamentale importanza per determinare il valore di un bene suscettibile di
fornire un reddito medio annuo costante e tendente all’infinito.
Sostituendo l’interesse nella formula generica del montante si ha:
![]() ;
; ![]() ;
;
da cui:
![]() ;
;
dove:
- “![]() ” è il coefficiente
di posticipazione ad interesse semplice; si usa per calcolare il valore
del capitale in un tempo futuro.
” è il coefficiente
di posticipazione ad interesse semplice; si usa per calcolare il valore
del capitale in un tempo futuro.
- “![]() ” è il coefficiente
di anticipazione ad interesse semplice; si usa per calcolare il valore
iniziale del capitale, o anche detto valore
scontato.
” è il coefficiente
di anticipazione ad interesse semplice; si usa per calcolare il valore
iniziale del capitale, o anche detto valore
scontato.
Graficamente:
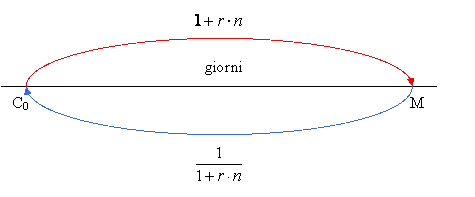
· Esempio 2
Essendo Tizio in possesso di una cambiale da 10.000 €, che scade tra 5 mesi, a quanto ammonta la somma che egli riscuoterebbe se la cambiale venisse scontata, in banca, al saggio dell’ 8%?
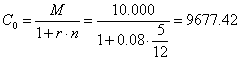 €
€
Giovedì 07/04/05
· Esempio 3
Quale è il montante di un capitale di 1.000 € per novanta giorni al saggio di interesse del 5%?
![]() €
€
Lunedì 11/04/05
Un valore riferito ad una determinata epoca non può essere addizionato o sottratto con un altro riferito ad un epoca diversa, se non quando ambedue i valori siano resi omogenei, e cioè riferiti alla stessa epoca; quindi ne consegue che uno dei due valori deve essere riportato all’epoca dell’altro oppure, che ambedue devono essere riportati ad una terza epoca. Tale spostamento di capitali nel tempo si raggiunge con i coefficienti di posticipazione o di anticipazione sia di interesse semplice che ad interesse composto.
Interesse composto
L’interesse composto annuo si ha quando l’interesse viene aggiunto al capitale che lo ha maturato alla fine di ogni anno, e viene adottato in tutte le applicazioni riguardanti tempi superiori ad un anno.
- Montante ad interesse composto
Per indicare il montante ad interesse composto si dice calcolare il montante comprensivo del capitale iniziale e dei relativi interessi composti maturati in un certo numero di anni.
![]() ;
; ![]() .
.
· Esempio 4
Siano dati 1.000 € impiegati a capitalizzazione composta con tasso di interesse del 4%, alla fine dell’anno quale sarà l’importo finale?
![]() €
€
Dove con Rt si indica il capitale nel tempo.
Alla fine del secondo anno si avrà:
![]() €
€
Sia dato un capitale nel tempo, e si vuole rapportarlo ad un altro tempo, naturalmente si adopererà lo studio precedente. Quindi si avrà:
![]() ;
;
![]() ;
;
iterando il procedimento fino all’n-esimo anno si avrà:
![]() ; se e solo se i = i1
= i2 . . . = in.
; se e solo se i = i1
= i2 . . . = in.
Dalle formule
generiche del montante,![]() e
e ![]() , si ricavano le seguenti espressioni:
, si ricavano le seguenti espressioni:
![]() ;
; ![]() ;
;
dove:
- “![]() ” è il coefficiente
di posticipazione ad interesse composto; si usa per calcolare il valore
del capitale in un tempo futuro.
” è il coefficiente
di posticipazione ad interesse composto; si usa per calcolare il valore
del capitale in un tempo futuro.
- “![]() ” è il coefficiente
di anticipazione ad interesse composto; si usa per calcolare il valore
iniziale del capitale, o anche detto valore
scontato.
” è il coefficiente
di anticipazione ad interesse composto; si usa per calcolare il valore
iniziale del capitale, o anche detto valore
scontato.
Graficamente:
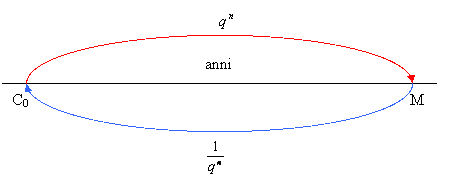
Lunedì 18/04/05
· Esempio 5
A quanto ammonterà fra 10 anni un capitale di 50.000 € depositato oggi in banca all’interesse del 4% ?
![]() €
€
· Esempio 6
Il diritto di realizzare tra 8 anni un credito di 100.000 € viene ceduto oggi ad una certa persona. Quale somma viene pagata attualmente supposto un saggio di sconto del 6% ?
![]() €
€
· Esempio 7
Depositando oggi in banca la somma di 100.000 € al saggio di interesse del 5%, quale sarà l’interesse maturato dopo 8 anni ?
![]() €
€
· Esempio 8
Tizio tra 4 mesi deve estinguere un debito di 20.000 €. Quanto dovrebbe pagare per liberarsi subito del suo debito? Saggio di sconto del 6%.
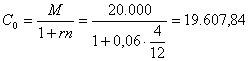 €
€
· Esempio 9
Tizio tra 5 anni deve estinguere un debito di 50.000 €, se volesse liberarsi oggi del suo onere, quanto dovrebbe sborsare? Tasso di interesse del 6%.
![]() €
€
Esercizi tipo esame
Normalmente si richiede un grafico temporale ( generalmente in anni ) del tipo in figura nel quale si chiede di determinare dove si ha l’interesse semplice, dove quello composto, e se i capitali indicati vengono riscossi a fine o inizio anno. Vediamo alcuni esempi.
- Esempio 1
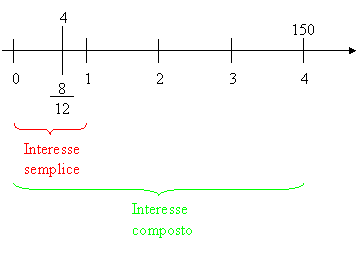
In questo caso si ha nel primo periodo un interesse semplice, e nel secondo un interesse composto, ma in entrambi la riscossione del valore monetario avviene a fine periodo.
□
- Esempio 2
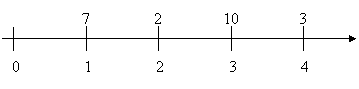 Anche in questo caso i valori monetari possono essere riscossi alla
fine di ogni singolo anno.
Anche in questo caso i valori monetari possono essere riscossi alla
fine di ogni singolo anno.
Inoltre si può notare che l’andamento del valore monetario presenta degli alti, primo e terzo anno, e dei bassi, secondo e terzo anno. □
- Esempio 3
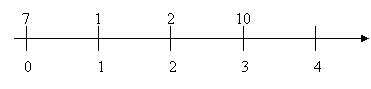 In questo caso, invece, i valori monetari vengono riscossi all’inizio
di ogni periodo. Questo si chiama annualità
.
In questo caso, invece, i valori monetari vengono riscossi all’inizio
di ogni periodo. Questo si chiama annualità
.
Non è detto che i valori considerati ogni anno devono essere per forza diversi ma possono essere anche uguali in ogni periodo; vediamo un esempio:
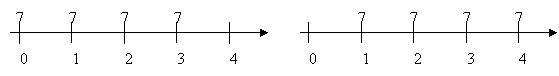
Quindi i valori monetari possono essere uguali o diversi.
Lunedì 02/05/05
Annualità
Distinguiamo quattro diversi tipi di annualità:
annualità costanti, posticipati, limitate;
annualità costanti, anticipate, limitate;
annualità costanti, posticipati, illimitate;
annualità costanti, anticipate, illimitate.
Il termine annualità sta ad indicare o dei debiti, o dei crediti, o il tasso di interessi, ecc.; insomma una qualunque cosa che si ripeta sempre con lo stesso valore. Le annualità si dicono:
a) costanti perché sono, in ogni periodo, sempre allo stesso modo, cioè uguali;
b) posticipate perché avvengono alla fine di ogni periodo, normalmente un anno;
c) limitate perché è indicato il numero finito di anni a cui si fa riferimento;
d) illimitate perché non è indicata il numero finito di anni a cui si fa riferimento.
Per rendere più chiare le idee vediamo come una rappresentazione del tipo:

sta ad indicare una annualità costanti, posticipati, limitate; mentre una rappresentazione del tipo:

sta ad indicare una annualità costanti, anticipate, limitate.
Naturalmente se si vuole determinare a priori o a posteriori quanto sarà l’ammontare totale, di un determinato periodo preso in esame, è necessario riportare tutti i valori uno ad uno o all’inizio, o alla fine del periodo totale.
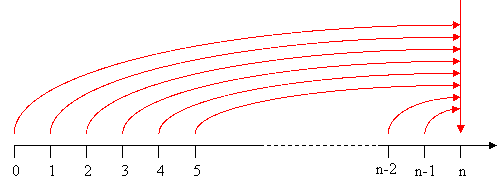 Supponiamo di voler determinare il valore totale calcolato alla fine
del periodo totale; allora per quanto detto sopra si avrà graficamente:
Supponiamo di voler determinare il valore totale calcolato alla fine
del periodo totale; allora per quanto detto sopra si avrà graficamente:
mentre matematicamente
si ha : ![]() , la quale è stata
ricavata dallo spostamento di ogni quantità ne tempo e precisamente tutti gli
spostamenti sono avvenuti verso la fine.
, la quale è stata
ricavata dallo spostamento di ogni quantità ne tempo e precisamente tutti gli
spostamenti sono avvenuti verso la fine.
Partendo da
![]()
mettendo in evidenza il fattore comune “a” cioè l’annualità, si ha
![]()
quindi osservando la parte presente si può concludere dicendo che essendo questa una processione geometrica crescente di regione “q”, essa avrà per soluzione la seguente espressione:
![]() .
.
Sostituendo nell’espressione di “An” si ha:
![]() .
.
Allo stesso modo si ragiona per determinare il valore totale calcolato all’inizio del periodo totale, per maggiore semplicità indichiamo ora ciò che si intende graficamente.
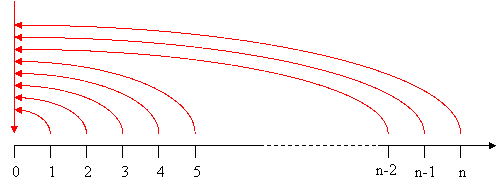
Risparmiamo il procedimento matematico perché del tutto uguale al precedente; indichiamo però solo la formula finale.
![]() .
.
- Accumulazione finale ( An )
Ogni qualvolta si
voglia determinare la somma riferita alla fine del periodo di una serie di
valori annui costanti e posticipati basterà moltiplicare l’importo
dell’annualità per il coefficiente: ![]() ,. Sono valori che si ripetono costantemente alla fine di
ogni anno per un determinato numero di anni; in particolare per “An” occorre
trasportare una ad una le singole annualità alla fine dell’anno “n” partendo da
quella che si verifica alla fine del periodo, ovvero un espressione aritmetica
in cui le diverse annualità si possono addizionare tra di loro perché riferite
alla stessa epoca e precisamente alla fine del periodo.
,. Sono valori che si ripetono costantemente alla fine di
ogni anno per un determinato numero di anni; in particolare per “An” occorre
trasportare una ad una le singole annualità alla fine dell’anno “n” partendo da
quella che si verifica alla fine del periodo, ovvero un espressione aritmetica
in cui le diverse annualità si possono addizionare tra di loro perché riferite
alla stessa epoca e precisamente alla fine del periodo.
Si osserva così che i termini tra parentesi costituiscono una progressione geometrica crescente di regione “q”.

- Accumulazione iniziale ( A0 )
L’accumulazione
iniziale si ottiene riportando una ad una, con
il coefficiente di sconto composto: ![]() , le singole annualità
all’anno zero ed eseguirne, data l’omogeneità dei valori, la somma aritmetica.
, le singole annualità
all’anno zero ed eseguirne, data l’omogeneità dei valori, la somma aritmetica.
Con un procedimento matematico analogo al precedente otteniamo:
![]()
e tale formula non è
altro che l’accumulazione finale riportata all’annualità con il coefficiente di
sconto composto ![]() .
.
In definitiva ogni qualvolta si voglia conoscere, all’anno zero, la somma
di più valori annui, costanti e posticipati, verificatosi per un determinato
numero di anni, basterà moltiplicare l’annualità data per il relativo
coefficiente: ![]() .
.
Ciò che è stato finora descritto è riferito alle annualità costanti posticipate limitate, vediamo ora le annualità costanti anticipate limitate.
• Le annualità costanti anticipate limitate differiscono dalle precedenti solo perché si verificano al principio di ognuno degli anni del periodo considerato.
Per trovare l’accumulazione finale ( An ) e l’accumulazione iniziale ( A0 ) non vi è che da applicare lo stesso procedimento già visto in precedenza, quindi basterà portare le singole annualità all’anno “n” per conoscere An e all’anno zero per conoscere A0.
Si può concludere dicendo che le annualità anticipate si verificano un anno prima di quelle posticipate; basterà quindi posticipare di un anno le annualità mediante il coefficiente di posticipazione annua “q” e quindi applicare gli stessi coefficienti di accumulazione relativi alle annualità costanti posticipate limitate.
Quindi si ha:
![]()
![]()
Se si hanno delle annualità e si posticipano di un anno allora An e A0 saranno spostati di tanto quanto è il periodo di posticipazione.
Giovedì 05/05/05
• Esempio 10
Per la maturazione straordinaria di un fabbricato il proprietario ha speso alla fine di ogni anno per quattro anni consecutivi 5.000 €. Si vuole conoscere la spesa complessiva riferita alla fine del periodo considerato. Sia r = 5%.
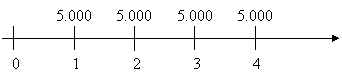
![]() €
€
• Esempio 11
Un agricoltore, in
seguito all’acquisto di una particolare macchina agricola, risulta debitore
verso
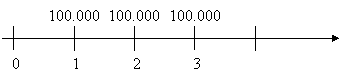
![]() €
€
• Esempio 12
Tizio per l’uso di un grosso supermercato che detiene in locazione paga un canone annuo di 30.000€ suddivise in tre rate anticipate. Le spese annue mediamente anticipate a carico della proprietà ammontano a 5.000 €. Si vuole conoscere il reddito annuo percepito dal proprietario del fabbricato. Sia r = 6%. Si determini poi anche il valore del fabbricato, supposto un saggio di capitalizzazione del 5%.
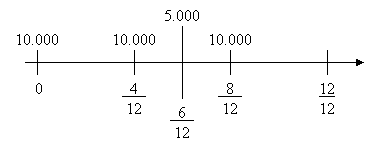
Dato che i valori presi in esame non sono uguali non possiamo parlare né di annualità né di accumulazione; pertanto si procede con le formule relative all’interesse semplice, perché siamo all’interno di un anno.
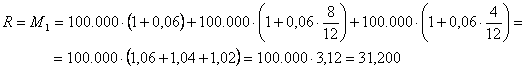
![]() €
€
![]() €
€
Reddito medio annuo posticipato = 26,050 €
Il reddito medio annuo coincide con l’interesse che ogni anno percepisce chi possiede un bene o una somma di denaro.
Per stimare il valore del fabbricato si usa la formula:
![]() €
€
Se “r”, saggio di capitalizzazione, è più piccolo significa che il bene ha delle caratteristiche intrinseche tali che il suo valore stimato sia tale da uguagliare il suo valore monetario.
□.
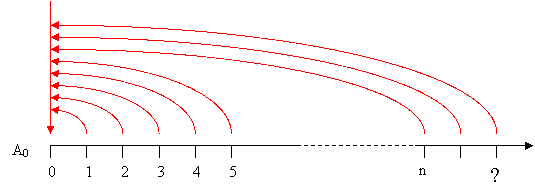
- Annualità costanti
posticipate illimitate (numero di anni molto elevati)
![]()
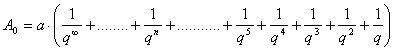
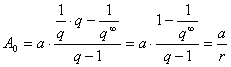
L’accumulazione finale non viene calcolata.
Nelle annualità costanti anticipate illimitate invece l’accumulazione iniziale è data da :
![]()
Le annualità costanti
posticipate illimitate sono valori che si ripetono costantemente alla fine di
ogni anno per un tempo infinitamente lungo. L’accumulazione finale non è
determinabile perché infinitamente grande e pertanto si presenta di fondamentale
importanza soltanto il problema dell’accumulazione iniziale che è uguale a: ![]() .
.
La formula sopra indicata è denominata formula di capitalizzazione, perché ogni qualvolta si divide il reddito netto perpetuo annuo, costante e posticipato di un capitale per il suo saggio di interesse, si ottiene il valore del capitale capace di generare tale reddito ( quindi sarà uguale a “V0”).
Quindi l’accumulazione iniziale di redditi tendenzialmente infiniti di un immobile corrisponde al suo valore capitale “V0”.
Per ottenere un capitale o il valore di un immobile basta dividere il suo reddito annuo netto costante ( oppure l’interesse annuo costante ) per un adeguato saggio di interesse denominato in questo caso saggio di capitalizzazione.
In altre parole il valore di un immobile aumenta con l’aumentare del suo reddito e con il diminuire del saggio di capitalizzazione.
Lunedì 09/05/05
• Esempio 13
Il proprietario di un fabbricato locato percepisce annualmente in media dall’inquilino un canone annuo complessivo posticipato di 5.000 €. Le spese medie annue complessive posticipate, sostenute dal proprietario dello stabile, ammontano a 1.600 €. Quale sarà il valore del fabbricato supponendo continua la durata della locazione e il saggio di capitalizzazione del 2%?
![]() €
€
![]() €
€
• Esempio 14
Un fondo fornisce mediamente una produzione annua lorda variabile di 80.000 €; le relative spese medie annue a carico del proprietario ammontano a complessivamente a 66.000 €. Si determini il valore del fondo. Sia r = 0,03 = 3%.
![]() €
€
![]() €
€
• Esempio 15
Un industriale per l’esecuzione di un particolare miglioramento immobiliare ha sostenuto ogni anno posticipatamente e per quattro anno consecutivi le seguenti spese:
1° anno . . . . . . . .....20.000 €
2° anno . . . . . . . .....50.000 €
3° anno . . . . . . . .....40.000 €
4° anno . . . . . . . .....70.000 €
Determinare la spesa media annua. Sia r = 0,06 = 6%.
![]() €
€
![]()
![]() €
€
- Quota di reintegrazione
La quota di reintegrazione, la quale si indica con il simbolo “Q/re” , è un valore che si deve mettere da parte per costituire un capitale desiderato.
![]()
Reintegrare un capitale
significa costituire, rinnovare, e formare un capitale in un determinato
periodo di tempo, pertanto quando si vuole conoscere la quota annua che si deve
accantonare in “n” anni per formare o rinnovare un determinato capitale “An”
basterà moltiplicare l’ammontare del capitale che si vuole costituire per ![]() che si trova calcolato
nelle tavole finanziarie.
che si trova calcolato
nelle tavole finanziarie.
- Quota di deprezzamento
La quota di deprezzamento è il prezzo medio di svalutazione che il capitale viene a subire annualmente per uso, consumo e progresso tecnico.
![]()
Dove “n” è la durata economica del capitale, per durata economica si intende il fatto che un capitale si usa solo finche esso risulta conveniente, a prescindere dalla sua utilizzazione per efficienza fisica, meccanica o fisiologica.
Gli scopi per cui si calcola Q/re e Qdep sono:
per quanto riguarda Q/re si usa per scopi finanziari ( quota di accantonamento per la formazione di un capitale );
- per quanto riguarda Qdep viene calcolata ai fini economico contabile ( quota di deprezzamento per il costo produzione ) ( ripartire il costo di un qualcosa nel tempo).
• Esempio 16
Tizio acquista una trattrice per il prezzo di 30.000 €. Supposta una durata economica di 12 anni e il valore residuo della macchina al 12° anno uguale a 5.000 € si vuol saper quanto dovrà tizio a annualmente accantonare per avere dopo 12 anni la somma necessaria per riacquistare la stessa trattrice e allo stesso prezzo. Sia r = 0,05 = 5%.
E quale sarebbe, invece, la corrispondente quota media annua di deprezzamento.
![]() €
€
![]() €
€
- Quota di ammortamento
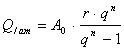
![]()
La quota di ammortamento è la rata annua o semestrale che si versa per estinguere un debito in un determinato numero di anni ad un prestabilito saggio di interesse, quindi la quota di ammortamento sarà comprensiva di capitale e di interesse, con il passare del tempo diminuisce la quota di interesse, mentre aumenta la quota di capitale, in modo tale, però, che la loro somma resti costante; pur rimanendo costante la rata la quota di capitale e quella di interesse, formanti la rata, nono solo saranno di diverso ammontare ma variano di anno in anno.
• Esempio 17
Un agricoltore acquista una trattrice per un valore di 40.000 €. Al momento della compravendita versa 10.000 € pattuendo di pagare la rimanenza in rate annue costanti per un periodo di tre anni e all’interesse del 7%. A quanto ammonta la rata del debito residuo.
![]() €
€
• Esempio 18
Supposto che un Istituto Bancario abbia concesso un mutuo di 20.000 € da estinguersi con rate da semestrali in 10 anni e al saggio del 6%, si vuole sapere:
a) la rata semestrale di ammortamento;
b)
Il tasso si divide
perché viene considerata la “semestralità” delle rate, di conseguenza le
rate raddoppiano.
il debito residuo subito dopo il pagamento della
14° rata.
![]()
a) ![]() €
€
b) ![]() € □.
€ □.
Giovedì 19/05/05
Esercizi tipo esami
- Esempio 4
Dato un grafico del tipo:
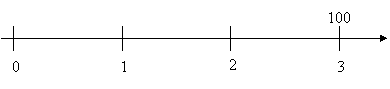
Determinare la quota di reintegrazione.
![]() □.
□.
- Esempio 5
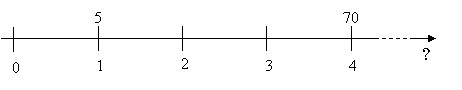 Dato un grafico del tipo:
Dato un grafico del tipo:
Determinare il valore all’anno 2.
Dato che dall’anno 3
sono presenti delle annualità costanti illimitate posticipate attraverso il
coefficiente ![]() si trova
l’accumulazione iniziale e poi con il coefficiente di anticipazione ad
interesse semplice o composto, perché in questo caso lo spostamento nel tempo è
sempre di un anno e quindi un coefficiente vale l’atro, si porta all’anno 2;
l’altro termine viene invece spostato normalmente. Quindi si ha che:
si trova
l’accumulazione iniziale e poi con il coefficiente di anticipazione ad
interesse semplice o composto, perché in questo caso lo spostamento nel tempo è
sempre di un anno e quindi un coefficiente vale l’atro, si porta all’anno 2;
l’altro termine viene invece spostato normalmente. Quindi si ha che:
![]() □.
□.
- Esempio 6
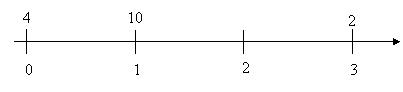 Dato un grafico del tipo:
Dato un grafico del tipo:
Determinare il valore totale all’anno 3.
![]() □.
□.
Lunedì 23/05/05
Esercizi tipo esami
- Esempio 7
Dato un grafico del tipo:
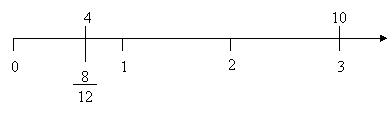 portare tutto all’anno 2.
portare tutto all’anno 2.

|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025