|
|
| |
TECNOLOGIA
Obiettivo dell'Impresa
E' un problema non banale
a) diversi tipi d'impresa: dal piccolo artigiano alla multinazionale
b) possibili conflitti d'interesse: azionisti, piccoli azionisti e management
L'impresa massimizza del profitto
profitto = ciò che resta alla proprietà dopo aver adempiuto a tutte le sue obbligazioni contrattuali
Profitto economico e non profitto contabile
tiene conto anche dei costi opportunità e quindi della remunerazione di tutti i fattori anche quello imprenditoriale
Costo opportunità di un fattore produttivo è uguale al valore delle risorse cui occorre rinunciare per renderlo disponibile
Profitto = Ricavi (entrate che l'impresa consegue vendendo i prodotti)
-Costi ( pagamenti per acquisire tutti gli inputs)
Vincoli dell'impresa
Tecnologico/Economico
Di mercato
Vincolo Tecnologico
La produzione di un'impresa obbedisce ad un ampio insieme di leggi inerenti alla chimica ed alla fisica, a principi ingegneristici, a moduli organizzativi codificati ed infine ad un insieme di procedure governate da conoscenze non codificate possedute dal suo personale

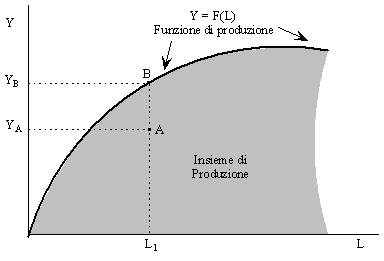
Insieme di produzione
Insieme di tutte le combinazioni di input ed output tecnicamente realizzabili
Nel caso di un impresa che produce un solo output utilizzando due inputs avremo che l'insieme di produzione di produzione dell'impresa è costituito dall'insieme Y di tutte le tecniche (y, L, K) cui l'impresa può avere accesso nella data situazione.
Funzione di produzione
Frontiera dell'insieme di produzione, equivale al massimo livello output che si può ottenere impiegando un dato livello degli inputs. Insieme che contiene esclusivamente tecniche efficienti
Ipotesi Tecnologia
a) La tecnologia è MONOTONA ovvero se si aumenta almeno uno degli inputs, e l'altro non diminuisce, si produce una quantità di output non inferiore e, se strettamente monotona, superiore. La funzione di produzione è crescente negli inputs
b)La tecnologia è CONVESSA ovvero se esistono due tecniche per produrre y (K1,L1) e (K2,L2) allora la loro media ponderata produrrà almeno y unità di output
Intervallo temporale di variazione degli input
fattore fisso
che non può essere liberamente variato nell'arco di un dato orizzonte temporale e si mantiene costante
fattore variabile
che può essere liberamente variato nell'arco di un dato orizzonte temporale
breve periodo
rappresenta un intervallo di tempo in cui uno o più fattori sono fissi e non c'è modo di modificarne l'impiego
lungo periodo
rappresenta un tempo sufficiente lungo per permettere all'impresa di modificare tutti i fattori produttivi a sua disposizione: tutti i fattori sono variabili
![]()
Nel caso di due fattori produttivi la funzione di produzione di breve periodo sarà
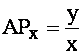 dove il capitale sarà il fattore fisso e il lavoro il
fattore mobile.
dove il capitale sarà il fattore fisso e il lavoro il
fattore mobile.
Prodotto medio di un fattore APx
rappresenta il prodotto per unità di fattore
Prodotto marginale di un fattore MPx
rappresenta l'aumento di output che si ottiene impiegando un unità addizionale di x
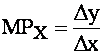
Per variazioni finite
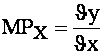
Per variazioni infinitesime
Nel breve periodo un input è fisso (il capitale è fisso) mentre l'altro (il lavoro) rimane variabile.
![]() La funzione di produzione ora è
La funzione di produzione ora è
|
Legge dei rendimenti marginali decrescenti |
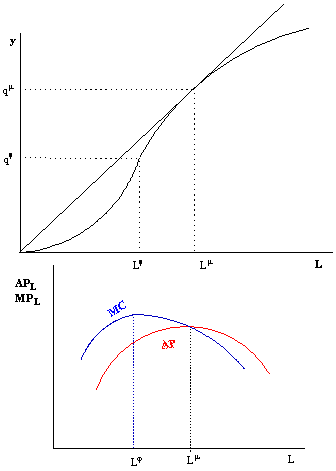
Aggiungendo quantità addizionali di un input e mantenendo costante la quantità degli altri fattori, il prodotto marginale prima cresce poi inizia a decrescere Ovviamente anche il prodotto medio prima cresce poi decresce |
|
Relazione fra AP e MP |
il prodotto medio sarà crescente/decrescente quando il prodotto marginale è maggiore/minore del prodotto medio e sarà massimo quando AP = MPx1 |
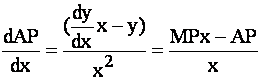
Derivando il prodotto medio rispetto a x
otteniamo
La funzione di produzione nel lungo periodo: gli isoquanti
Consideriamo una tecnologia descritta da una funzione di produzione y = F(K, L).
Come rappresentarla graficamente in uno spazio bidimensionale ?
Per ogni data quantità di output, ad esempio , possiamo chiederci quali siano le coppie di valori (K, L) che sulla base della tecnologia in questione, consentano di ottenere la stessa la quantità di output.
Formalmente, se
ipotizziamo che sia possibile utilizzare solo quantità positive o nulle
(non negative) di ogni fattore, l'isoquanto della funzione
di produzione f(K,L) è costituito dall'insieme di punti (K, L) nello
spazio L, K tali che

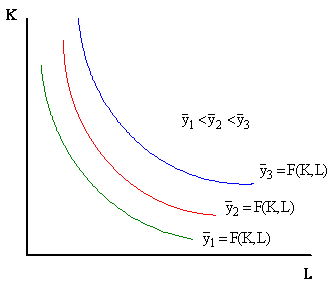
Definizione di Isoquanto
Luogo geometrico delle combinazioni dei fattori produttivi che generano un medesimo livello di produzione
|
Proprietà degli isoquanti |
Sono negativamente inclinati Per l'ipotesi di monotonicità della funzione di produzione |
|
Non possono intersecarsi Sempre per la monotonicità |
|
|
Dati due livelli produttivi, l'isoquanto associato al livello produttivo maggiore giace a destra dell'isoquanto associato al livello minore |
|
|
Sono convessi se la tecnologia è convessa e la funzione di produzione concava |
calcoliamo il differenziale totale della funzione di produzione otteniamo
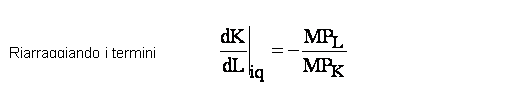
![]()
L'inclinazione dell'isoquanto prende il nome di Tasso Marginale di Sostituzione tecnica (MRTS)
MRTS valutato in un punto (L,K)
Indica l'ammontare del fattore K con cui è possibile compensare una variazione infinitesima del fattore L in modo da mantenere costante il livello della produzione
Rendimenti di Scala
Cosa succede al prodotto se tutti i fattori variano dello stesso ammontare, ovvero se varia la scala della produzione?
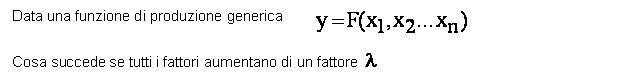
|
Crescenti |
L'output cresce più che proporzionalmente rispetto alla crescita degli inputs |
|
Costanti |
L'output cresce proporzionalmente rispetto alla crescita degli inputs |
|
Decrescenti |
L'output cresce meno che proporzionalmente rispetto alla crescita degli inputs |
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026