|
|
| |
Le aspettative (e = atteso; π = inflazione)
Introduciamo una dimensione intertemporale. Nei modelli analizzati sinora abbiamo immaginato che i P siano fissi e l'inflazione non esista, mentre i reale = i nominale - inflazione
C = c0 + c1 Yd
Il consumo odierno dipende anche dai redditi passati e dalle aspettative per il futuro.
Questo è ancora più vero per quanto riguarda I = I0 + d1Y - d2i e Md/P = f1Y - f2i
Tasso di interesse reale e tasso di inflazione atteso
rt = tasso di interesse reale al tempo t
it = tasso di interesse nominale al tempo t
(1 + rt) ≡ (1 + it) * Pt / Pet+1
dove Pt esprime il livello ottimale dei prezzi, mentre Pet+1 il livello attesa al tempo t+1.
Se i P non cambiano: Pt/Pet+1 = 1
Se i P aumentano: Pt/Pet+1 < 1
Se i P diminuiscono: Pt/Pet+1 > 1
Pet+1 - Pt
πet ≡ ----- ----- --------- variazione futura dei prezzi diviso il livello attuale dei P. =>
Pt
Pt + Pet+1 - Pt Pet+1
=> 1 + πet = ----- ----- --------- = ----- ----- ----- =>
Pt Pt
1 Pt
=> ------------ = ---------- =>
1 + πet Pet+1
![]() 1 + it
1 + it
=> (1 + rt) = ----------- => (1 + rt) (1 + et) = 1 + it => 1 + rt + et + rt * et = 1 + it => rt ≈ it - et
1 + πet
L'equazione finale dice che il tasso di interesse reale è ≈ al tasso di interesse nominale, meno l'inflazione attesa
I due tassi sono uguali solo quando l'inflazione è nulla.
Quanto più elevato è il tasso di inflazione, minore è il tasso di interesse reale.
Se misuriamo il livello dei prezzi con l'indice dei prezzi ai consumo (CPI), il tasso di interesse reale ci dice a quanto consumo dovremo rinunciare domani per consumare di più oggi.
Valore presente scontato atteso = valore attuale
Il problema dell'imprenditore è quello di valutare se il valore dei profitti attesi è superiore al costo di acquisto del macchinario. Il valore attuale di una sequenza di pagamenti è il valore oggi di questa sequenza attesa di pagamenti.
Il valore attuale di un Dollaro l'anno prossimo è 1/(1 + it). Questa formula è chiamata fattore di sconto,
dove it è il tasso di interesse nominale chiamato tasso di sconto.
Problemi di capitalizzazione e di sconto
Il problema della capitalizzazione pone, sostanzialmente questo quesito: se oggi hai TOT, dato un tasso d'interesse e di inflazione, quanto varranno al tempo t + x? E qual è il valore oggi di un titolo che dà un certo interesse?
Da questi quesiti sorgono problemi di sconto e di capitalizzazione.
Definizione di costo opportunità: è il valore che si perde mantenendo il proprio capitale in moneta anziché investito in titoli (su cui si generano gli interessi).
A questo punto ci chiediamo quale tra rt e it devo usare nella IS-LM
Il tasso di interesse influenza l'investimento nella curva IS e influisce sulla scelta tra moneta e titoli nella LM.
|
Curva IS |
(beni, imprese) |
Valore rilevante: r |
|
Curva LM |
(inflazione, valore della moneta) |
Valore rilevante: i |
Analizziamo lo schema: nel decidere l'ammontare del loro investimento, le imprese sono interessate al tasso di interesse reale, ossia a quanto dovranno ripagare in termini di beni (vedi, ad es., prestiti bancari a tasso fisso), quindi per quanto riguarda la curva IS, il valore rilevante sarà r (tasso di interesse reale): Y = C(Y - T) + I(Y, r) + G
In altre parole, la domanda di beni dipende dal tasso di interesse reale.
Per quanto riguarda la curva LM, il valore rilevante sarà i (intereresse nominale), poiché la politica monetaria è interessata al tasso nominale: M/P = YL(i) => M/P = YL(r + πe).
L'inflazione, infatti, guarda al valore d'acquisto della moneta. Il costo opportunità di detenere moneta è uguale a i.
Nota πe = 0 i = r nessuna variazione della curva IS-LM
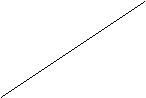
πe > 0 i ≠ r variazione come da grafico seguente:
![]()
![]()
![]() LM
LM
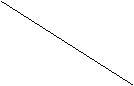
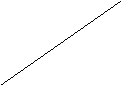 LM'
LM'
r E0
![]()
![]()
![]()
![]() Δ
πe r' E'
Δ
πe r' E'
![]() r"
Δi A A"
r"
Δi A A"
IS
![]()
1000 Y0 Y1 Y
Precisazione sul Blanchard:
![]() r ↓ => I ↑ => Z ↑
=> Y ↑ => Md/P ↑ => i ↑
r ↓ => I ↑ => Z ↑
=> Y ↑ => Md/P ↑ => i ↑
Questo è vero soltanto se i prezzi sono fissi!
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026