|
|
| |
(24 novembre 2003)
La crescita di un'economia è descritta dalle seguenti relazioni, in cui H esprime la quantità di capitale umano che è posta uguale alla quantità di lavoro misurata in termini di efficienza:
![]()
![]()
![]()
![]()
![]()
i) Posto ![]() , ricavate la quantità di capitale per lavoratore, misurato
in termini di unità di efficienza, di stato uniforme. (Ponete
, ricavate la quantità di capitale per lavoratore, misurato
in termini di unità di efficienza, di stato uniforme. (Ponete ![]() e
e ![]() ; risolvete quindi l'equazione di Solow che definisce la
condizione di stato uniforme.)
; risolvete quindi l'equazione di Solow che definisce la
condizione di stato uniforme.)
ii) Ricavate il sentiero di stato uniforme della quantità di capitale per lavoratore, misurato in termini di unita fisiche.
iii) Ricavate il prodotto per lavoratore, misurato in unità fisiche, lungo la traiettoria di stato uniforme e il suo tasso di crescita.
2. Supponete ora un'economia a due settori, il primo dei quali produce
beni e servizi, il secondo capitale umano. Sia ![]() la quantità di
capitale umano di ogni lavoratore e
la quantità di
capitale umano di ogni lavoratore e ![]() la quota percentuale
dei lavoratori dedicata alla produzione di beni e servizi. Supponete che la
produzione di beni e servizi richieda l'impiego di capitale fisico ed umano
secondo la relazione
la quota percentuale
dei lavoratori dedicata alla produzione di beni e servizi. Supponete che la
produzione di beni e servizi richieda l'impiego di capitale fisico ed umano
secondo la relazione
![]() con (2')
con (2') ![]()
mentre la produzione di nuovo capitale umano richiede l'uso di solo capitale umano secondo la relazione
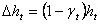
Queste tre relazioni sostituiscono le prime tre del modello precedente, mentre restano immutate le successive due.
i) Sia ![]() la quota percentuale
costante del lavoro dedicata alla produzione di beni e servizi in stato
uniforme. Tenuto conto che in stato uniforme devono inoltre essere uguali e
costanti i tassi di variazione del prodotto per lavoratore e del capitale per
lavoratore, mostrate che questi coincidono con il tasso di crescita del
capitale umano per lavoratore. (Utilizzate la scomposizione del tasso di
crescita nel prodotto nella somma dei tassi di crescita del capitale fisico e
del capitale umano.)
la quota percentuale
costante del lavoro dedicata alla produzione di beni e servizi in stato
uniforme. Tenuto conto che in stato uniforme devono inoltre essere uguali e
costanti i tassi di variazione del prodotto per lavoratore e del capitale per
lavoratore, mostrate che questi coincidono con il tasso di crescita del
capitale umano per lavoratore. (Utilizzate la scomposizione del tasso di
crescita nel prodotto nella somma dei tassi di crescita del capitale fisico e
del capitale umano.)
ii) Determinate il sentiero del tasso di crescita del prodotto per
lavoratore con ![]() .
.
iii) Supponete che un'economia sia in grado di realizzare un aumento
della quote del lavoro destinato alla produzione di capitale umano - aumenta ![]() . Descrivete i processi che si determinano in tale economia a
seguito di tale cambiamento.
. Descrivete i processi che si determinano in tale economia a
seguito di tale cambiamento.
3. Spiegate il concetto di tasso di disoccupazione di equilibrio. Mostrate le implicazioni per il funzionamento del mercato del lavoro dei diversi approcci a tale concetto.
Mankiw (3a ed., cap. 4, p. 59) e Blanchard (cap. 11, p. 291) esaminano un'applicazione numerica del modello di Solow con riferimento al caso di assenza di progresso tecnico e sulla base di una funzione della produzione di tipo Cobb-Douglas. Questo esercizio mira ad estendere quelle applicazioni al caso di progresso tecnico.
i) Siano
![]() e
e ![]()
rispettivamente il prodotto per lavoratore e il capitale per lavoratore quando il lavoro è misurato in unità di efficienza. Per l'ipotesi di rendimenti costanti di scala, la funzione di produzione può essere espressa in termini intensivi utilizzando queste grandezze; si ha
![]()
Anche la relazione che definisce la variazione dello stock di capitale
può essere convenientemente formulata in termini intensivi; dividendo tutti i
termini della (5) per ![]() e tenendo conto della
(1.2) si ottiene
e tenendo conto della
(1.2) si ottiene
![]()
Dalla definizione di ![]() nella (1.1), si
ottiene
nella (1.1), si
ottiene
![]()
Ne segue che la relazione fra i tassi di crescita di queste grandezze è
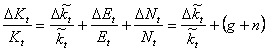
dove g ed n sono i tassi di crescita
dell'efficienza (progresso tecnico) e del lavoro, costanti nel tempo come
risulta dalle equazioni (3) e (4) del modello; ovviamente la somma di tali
grandezze è il tasso di crescita del lavoro misurato in unità di efficienza.
Moltiplicando entrambi i lati della (1.5) per ![]() e tenendo conto della
relativa definizione, si ricava infine
e tenendo conto della
relativa definizione, si ricava infine
![]()
Possiamo ora sostituire la (1.6) nella (1.3) ed otteniamo così l'equazione di Solow che descrive la variazione dello stock di capitale per lavoratore misurato in unità di efficienza
![]()
In stato uniforme ![]() deve rimanere
costante. Possiamo pertanto risolvere la (1.7) ponendo
deve rimanere
costante. Possiamo pertanto risolvere la (1.7) ponendo ![]() ; si ottiene
; si ottiene
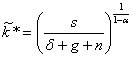
e inserendo i valori dei parametri indicati
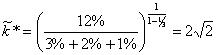
ii) Definiamo il rapporto tra capitale e lavoro misurato in unità fisiche; tenuto conto della definizione (1.1) e con riferimento allo stato uniforme, si ha
![]()
La (1.10) descrive dunque il sentiero di crescita di stato uniforme di
tale grandezza che, a differenza di ![]() , non rimane costante ma cresce al tasso g, che è il tasso di crescita dell'efficienza, ossia del progresso
tecnico.
, non rimane costante ma cresce al tasso g, che è il tasso di crescita dell'efficienza, ossia del progresso
tecnico.
iii) Anche il prodotto per lavoratore misurato in unità fisiche cresce al tasso g come si può dedurre immediatamente dalla definizione
![]()
In questo esercizio si suppone che la crescita dell'efficienza del lavoro, cioè del capitale umano di ogni lavoratore, dipenda dalla quota del lavoro dedicata al settore dell'istruzione, come indicato dalla relazione (3').
i) Dalla funzione
della produzione possiamo ricavare, secondo lo schema della contabilità della
crescita, la seguente relazione fra tassi di variazione percentuale del
prodotto ![]() , del capitale fisico
, del capitale fisico ![]() e del capitale umano
e del capitale umano ![]() :
:
![]()
Tenuto conto
che in stato uniforme per la (2') ![]() e che per la (3')
e che per la (3') ![]() . Si ha
. Si ha
![]()
Definendo ora i
tassi di variazione del prodotto per lavoratore ![]() e del capitale per lavoratore
e del capitale per lavoratore ![]() misurati in unità fisiche, la (2.2) può essere riscritta come
segue
misurati in unità fisiche, la (2.2) può essere riscritta come
segue
![]()
Ma in stato uniforme i tassi di crescita del prodotto per lavoratore e del capitale per lavoratore devono essere uguali; imponendo tale condizione si ottiene
![]()
che mostra come anche nello schema teorico in esame queste grandezze crescono al tasso di crescita del "progresso tecnico", ora indicato come capitale umano, e come quest'ultimo dipende dalla quota del lavoro destinato all'attività di produzione di capitale umano.
ii) Definiamo ![]() e
e ![]() come nelle precedenti
equazioni (1.1) e riformuliamo la funzione di produzione in termini intensivi
come segue
come nelle precedenti
equazioni (1.1) e riformuliamo la funzione di produzione in termini intensivi
come segue
![]()
Con procedimento analogo al precedente, l'equazione di Solow risulta quindi essere
![]()
Risolvendo per lo stock di capitale di stato uniforme si ottiene
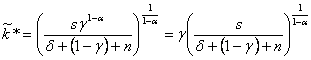
Sostituendo i valori assegnati ai parametri, si ha
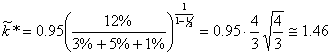
iii) Supponiamo che
vi sia un aumento permanente di ![]() , ossia della quota del lavoro destinato alla formazione di
capitale umano. L'effetto sul valore di stato uniforme del rapporto fra
capitale fisico e capitale umano è identico a quello che si verifica nel
modello di Solow con progresso tecnico esogeno, e precisamente una diminuzione,
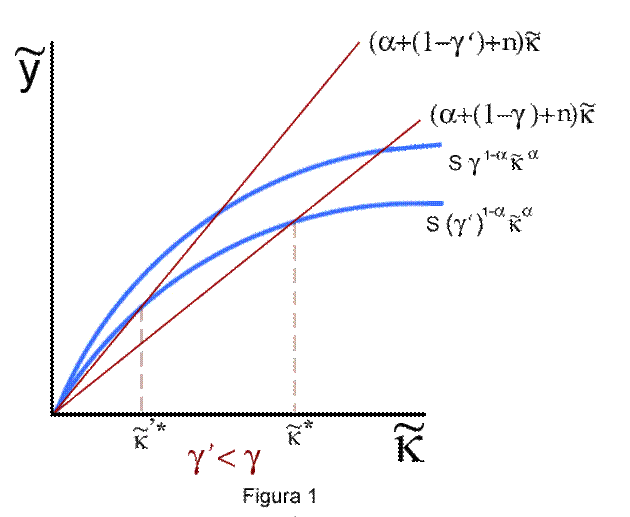
come si vede dalla Fig. 1 in cui l'intercetta fra la curva che descrive gli
investimenti resi possibili dal risparmio e la retta che rappresenta gli
investimenti necessari a mantenere invariato il rapporto fra capitale fisico e
capitale umano si sposta verso sinistra. Ne segue che anche il prodotto per
lavoratore, in termini di capitale umano, di stato uniforme diminuisce.
, ossia della quota del lavoro destinato alla formazione di
capitale umano. L'effetto sul valore di stato uniforme del rapporto fra
capitale fisico e capitale umano è identico a quello che si verifica nel
modello di Solow con progresso tecnico esogeno, e precisamente una diminuzione,
come si vede dalla Fig. 1 in cui l'intercetta fra la curva che descrive gli
investimenti resi possibili dal risparmio e la retta che rappresenta gli
investimenti necessari a mantenere invariato il rapporto fra capitale fisico e
capitale umano si sposta verso sinistra. Ne segue che anche il prodotto per
lavoratore, in termini di capitale umano, di stato uniforme diminuisce.
Se si considerano invece gli effetti sul capitale e sul prodotto per lavoratore misurato in termini di unità fisiche, per comprendere quanto accade è necessario riprendere le precedenti definizioni (1.10) e (1.11). Dalla prima, si ha
![]()
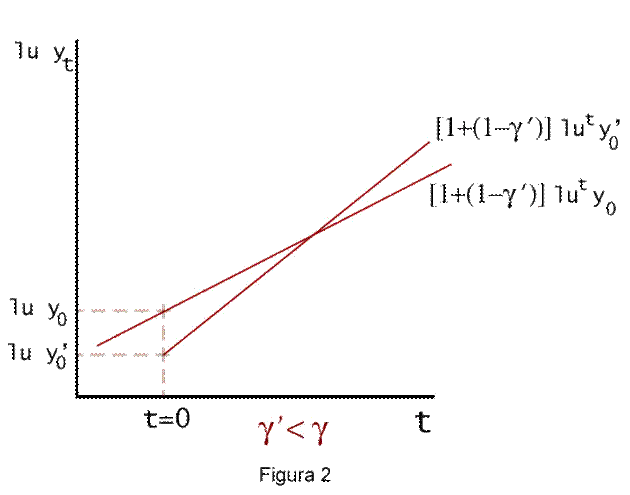
Si è quindi in
presenza di due effetti di segno opposto: da un lato, diminuisce ![]() ; dall'altro, l'efficienza cresce più rapidamente. Poiché
quest'ultimo termine dipende dal tempo, è chiaro che quanto più lontano è
l'orizzonte temporale considerato, tanto maggiore la probabilità che il secondo
effetto prevalga sul primo. Un aumento del tasso di crescita del capitale umano
è quindi destinato a determinare un livello di prodotto per lavoratore più
elevato, nonostante la iniziale caduta, come indicato nella Fig. 2.
; dall'altro, l'efficienza cresce più rapidamente. Poiché
quest'ultimo termine dipende dal tempo, è chiaro che quanto più lontano è
l'orizzonte temporale considerato, tanto maggiore la probabilità che il secondo
effetto prevalga sul primo. Un aumento del tasso di crescita del capitale umano
è quindi destinato a determinare un livello di prodotto per lavoratore più
elevato, nonostante la iniziale caduta, come indicato nella Fig. 2.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026