1 2

+

V_al L

V

L: lampadina

A: amperometro

V: voltmetro

R : reostato(usato come regolatore di tensione )

V_al : alimentazione in continua

1 : Voltmetro a monte

2 : Voltmetro a valle

Apparecchiature utilizzate

Alimentazione in continua a 70 V ;

Reostato di tipo lineare semplice 406/s ,resistenza 100 W , corrente max 2.5 A ;

Voltmetro : strumento analogico elettromeccanico magnetoelettrico per continua;

a magnete fisso, bobbina mobile, a quadrante orizzontale,

classe 0,5; consumo 200 W/V , fondo scala variabile 75 V,150V,

300V,n. divisioni a fondo scala : 150

Amperometro : tipo magnetoelettrico per continua, classe 0.5 , 150 divisioni f.s. , usato con i seguenti shunt : officine Galileo , 60 mV , 6W , 2A ;

officine Galileo , 60 mV , 6W , 1A ;

officine Galileo , 60 mV , 6W , 500 mA ;

officine Galileo , 60 mV , 6W , 200 mA ;

Lampadina con i seguenti dati di targa: potenza nominale 25 W, tensione nominale 125-130 V

Esecuzione della misura  

Prima di iniziare la nostra misurazione abbiamo calcolato l'effetto dell'errore di consumo sulla misura stessa : infatti se quest'ultimo non è trascurabile o almeno dello stesso ordine rispetto alla somma delle incertezze relative agli strumenti rivelatori in questione (voltmetro e amperometro ) non conviene eseguire la misurazione .

Gli errori di consumo sono dovuti all'utilizzo di strumenti di natura elettromeccanica, poiché le resistenze interne non sono sufficientemente elevate nei voltmetri e basse negli amperometri .

Per valutare l'errore di consumo ci dobbiamo riferire alle due possibili inserzioni del voltmetro : a valle o a monte dell'amperometro .

Infatti il voltmetro inserito a monte indica la somma delle tensioni su R_L e su R_a (resistenza interna dell'amperometro ),anziché solo la caduta di tensione su R_L ,il che comporta un errore di consumo pari a :

e_a = ;

nel caso di voltmetro a valle invece è l'amperometro a commettere un errore perché esso indica la somma delle correnti che passano per R_L e per R_v (anziché solo la corrente nella lampadina) e si ha un errore di consumo pari a :

e_v

Per una stima degli errori di consumo si fa riferimento ai valori di targa della lampadina : V= 125 V e P = 25 W .

Da questi valori si ricava una corrente nominale per la lampadina pari a I_nom=P/V=0.2 A

da cui si ha R_nom W

Con tali valori si sceglie lo shunt da 200 mA e un fondo scala di 150 V per il voltmetro e otteniamo : R_a W

R_V =consumo* f.s. scelto 30000 W

e_v = 2%

e_a = 0,03% .

Le incertezze dovute alla classe degli strumenti valgono :

e_A=c_A* I_fs/I_l= 0.5%

e_V=c_V* V_fs/V_l= 0.6%

ed essendo R=V/I si ottiene :

e_R e_V e_A

Si osserva che e_a << e_R e e_V e_R e allora ha senso compiere la misura ; si preferisce l'inserzione con voltmetro a monte poiché l'errore di consumo risulta essere trascurabile, essendo un ord 111e49b ine di grandezza inferiore rispetto a quello dell'errore di classe . In tale configurazione non si opera dunque una correzione , necessaria invece per l'inserzione a valle.

Ipotesi di lavoro semplificative

Ipotizziamo di trascurare le variazioni della temperatura ambiente in cui si opera ; essa risulta essere di circa 21⁰C all'inizio dell'esperienza e quindi non è necessario correggere la classe degli strumenti poiché per essi la classe è garantita per 20 2⁰C . In realtà la temperatura dell'ambiente è variata nel corso dell'esperienza (raggiungendo i 24⁰C alla fine dell'esperienza) e sarebbe stato opportuno un controllo continuo di essa .

Inoltre si trascura l'effetto delle resistenze di contatto e quelle di dispersione in quanto le prime sono dell'ordine dei mW (mentre l'incertezza calcolata è dell'ordine dell' W ) e le seconde intervengono nel caso di resistenze dell'ordine dei MW .

Infine si trascura l'effetto Seebeck poiché introduce variazioni di resistenze dell'ordine dei mW .

Esecuzione della misura - voltmetro a monte

Montiamo il circuito secondo lo schema del voltmetro a monte .

Scegliamo di eseguire la misurazione procedendo con tensioni crescenti, con incrementi successivi di 10 V, iniziando così con il reostato tutto inserito. Inizialmente optiamo per un fondo scala del voltmetro pari a 75 V, in modo da lavorare per quanto possibile vicino al fondo scala (errore di classe minimo).

Per l'amperometro usiamo uno shunt da 200mA , poiché è questa la portata minima a disposizione . Ci accorgiamo che a reostato tutto inserito non riusciamo ad arrivare al valore di tensione nominale per la lampadina pari a 125V , in quanto l'alimentazione disponibile è in realtà inferiore a 140 V . Sono riportati di seguito i valori di tensione e di corrente letti e i valori di resistenze calcolati secondo il modello approssimato :

R= V/I

(nella tabella sono riportati i valori dei calcoli intermedi, per i valori conclusivi si veda il paragrafo « Risultati conclusivi-voltmetro a monte «)

Diario - voltmetro a monte - R,P

Nella tabella sono riportati il valore delle tacche lette, la portata e il valore ottenuto attraverso la costante strumentale per ogni lettura eseguita. Per un controllo dei risultati la misura è stata eseguita ripercorrendo per valori di tensione decrescenti i punti calcolati . E' stata inoltre riportato il valore della potenza assorbita dalla lampadina P=R*I² .

Stima delle incertezze

Assunto il valore della resistenza pari a R=V/I , con il modello deterministico , l'incertezza è : e_R e_V e_A , pari alla somma degli errori di classe degli strumenti . Come già detto , l'errore di consumo è trascurabile però bisogna ancora valutare l'errore assoluto dovuto alla lettura.Esso si assume pari a 1/4 di divisione. L'errore relativo sarà :

e_lett=0.25*K/V_l*100

dove K= portata/n.ro div. a f.s. e V_l è il valore letto .

I vari errori relativi sono riportati in tabella e possiamo notare come assumano valori più alti nel casi di misure eseguite con indice lontano dal fondo scala .

(nella tabella sono riportati i valori dei calcoli intermedi, per i valori conclusivi si veda il paragrafo « Risultati conclusivi-voltmetro a monte «)

voltmetro a monte - errori

Risultati conclusivi - voltmetro a monte

Riportando i dati conclusivi solo per valori di tensione crescenti (pressoché uguali a quelli per tensioni decrescenti) ,tenendo conto delle opportune approssimazioni

derivanti dalla stima degli errori si ottiene la seguente tabella.

Si osservi che l´incertezza relativa e' la stessa sia per la resistenza che per la potenza, perche´ per entrambe si sommano le incertezze relative sulla misura di tensione e di corrente :

A questo punto è possibile tracciare i diagrammi che ci eravamo proposti R=F(V) ,    R =F(P) ed inoltre possiamo tracciare l'andamento dell'errore relativo DR/R=f(I) .

I grafici ottenuti sono riportati nelle ultime pagini della relazione .

Esecuzione della misura - voltmetro a valle

Si è ripetuta la misura cambiando inserzione , cioè ponendo il voltmetro a valle dell'amperometro .

I risultati ottenuti sono riportati nelle tabella successiva . In questo caso , come già discusso , non è trascurabile l'errore di consumo dovuto al voltmetro ed è necessario apportare una correzione al valore di resistenza ottenuto conoscendo il valore di resistenza interna del voltmetro:

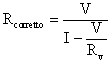
ove V e I sono le indicazioni del voltmetro e dell´amperometro e R_v e´ la resistenza interna del voltmetro.

Tuttavia essendo la resistenza interna degli strumenti nota a meno di una incertezza, la correzione sarebbe solo parziale e si avrebbe comunque un contributo di incertezza dovuto al consumo; si osserva che questo termine di incertezza è trascurabile rispetto agli altri perché circa pari al 10% dell'errore relativo di consumo.

(nella tabella sono riportati i valori dei calcoli intermedi, per i valori conclusivi si veda il paragrafo « Risultati conclusivi-voltmetro a valle «)

Diario - voltmetro a valle - R,P

Nella tabella seguente sono riportati i singoli errori e l errore totale. Si noti come nel calcolo di e_totale% non venga considerato l errore di consumo (e_V) perché gia´ corretto in precedenza.

(nella tabella sono riportati i valori dei calcoli intermedi, per i valori conclusivi si veda il paragrafo « Risultati conclusivi-voltmetro a valle «)

voltmetro a valle- incertezze

Risultati conclusivi - voltmetro a valle

Analisi dei risultati

Dai risultati ottenuti si nota come la resistenza della lampadina vari al variare della tensione e della corrente ; possiamo attribuire questo fatto al riscaldamento del filamento .

Si ha infatti una variazione di resistenza da R=150 W (per V=10 V) a R=660 W (per V=130 V).

Questa differenza poteva essere grossolanamente stimata da semplici considerazioni fisiche: dai dati nominali della lampadina si trova che a V=125 V R 600 W . Se si suppone che la resistenza vari esclusivamente con la temperatura e che dissipi tutta l'energia assorbita per irraggiamento allora è possibile trattare la lampadina come un corpo nero.

In questo modo è possibile stimare la temperatura del filamento dal colore dell'emissione: in particolare in condizioni nominali la lampadina emette una luce bianco-gialla a cui corrisponde una temperatura di corpo nero di circa 2000 °C.

Applicando la legge di variazione della resistenza con la temperatura sviluppata al primo ordine (le approssimazioni fatte sono già molto grossolane !) si ricava che a temperatura ambiente la R_L W

Questo valore può sembrare molto differente da quello trovato nella prova 1 ma in realtà esso si riferisce alla lampadina a riposo mentre nella prova suddetta si ha una piccola circolazione di corrente che inevitabilmente fa aumentare la temperatura ( e quindi la resistenza) della lampadina stessa.

Si osserva inoltre che i dati ricavati dalla prova con voltmetro a monte e voltmetro a valle sono compatibili tra di loro.

La funzione DR/R=f(I) è monotona decrescente a tratti : questo perché il suo andamento è influenzato dagli errori di classe degli strumenti. In particolare si nota che in corrispondenza del cambio di portata del voltmetro si ha un aumento dell'errore relativo: in questo tratto , infatti, l'indice si sposta verso sinistra con conseguente aumento dell'errore di classe confermando quanto detto in precedenza e cioè che per avere piccoli errori di classe è bene lavorare il più possibile vicino al fondo scala degli strumenti.