10.1.1 Ciclo di Rankine - Hirn

vaporizzazione dell'acqua (p_c 226 bar, p > p_c ciclo ipercritico) seguita, in genere, dal surriscaldamento del vapore;

espansione (praticamente adiabatica) del vapore, con fornitura di lavoro agli organi mobili del motore;

saturazione di calore al vapore scaricato dal motore (condensazione).

figura 10.1

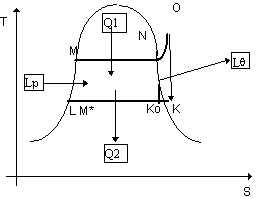
figura 10.2

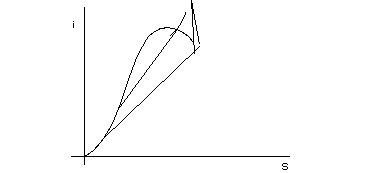
figura 10.3

Trattandosi di un ciclo reale, si considerano le trasformazioni medie che il fluido subisce nei vari organi dell'impiant 838d36i o. In particolare la linea OK di espansione in turbina rappresenta mediamente le condizioni del vapore nei vari "elementi" o "stadi" della macchina.

L'effetto della viscosità del fluido, per cui, sostanzialmente, il ciclo reale LMNOK differisce da quello reversibile LMNOK_is, è rilevante solo nella turbina. Nelle altre parti esso è, in genere, trascurabile.

Trascureremo inoltre le perdite di carico nelle tubazioni di collegamento fra le varie parti dell'impianto, nel genereatore di vapore, ecc.

La fase di compressione del fluido per mezzo della pompa P_e (di estrazione della condensa) e P_a (di alimento) non è distinguibile nel diagramma i,S (e ancor meno in quello T,S) in quanto di solito la scala con cui si opera è troppo piccola per rendere visibile il tratto LM^* (che si considera in genere isoentropico).

figura 10.4

Pertanto si usa confondere la spezzata LM^*M con il tratto di curva limite LM, tenendo però presente che nella fase di riscaldamento del liquido cresce solo la temperatura mentre sulla curva limite inferiore pressione e temperatura variano in accordo con le condizioni di saturazione.

Il lavoro massico fornito dal fluido lungo il ciclo è pari alla differenza tra il lavoro di espansione, L, nella turbina e il lavoro di compressione, L_p, nelle pompe:

L = L - Lp

Dal I principio della termodinamica applicato tra ingresso ed uscita della turbina:

Q_e - L = i + E_c

Ma Q_e = 0 e siccome E_c << L: L = - i = i₀ - i_k

Per la pompa, essendo E_c 0 e g z 0: L_p = i_M* - i_L

Quindi: L = i₀ - i_K - (i_M* - i_L) i₀ - i_k

il calore massico fornito al fluido risulta:

Q₁ = i₀ - i_M* i_o - i_L

mentre il calore sottratto: Q₂ = i_K - i_L

da queste relazioni si verifica che: L = Q₁ - Q₂

Il rendimento del ciclo, rapporto tra il lavoro ottenuto in un ciclo (sommatoria algebrica dei lavori fluido macchina) e la quantità di calore fornita al fluido, vale:

=

In genere si trascura, nel calcolo del rendimento del ciclo,il lavoro di compressione (L L₎ e se ne tiene conto nel rendimento organico, considerando le pompe (di estrazione condensa e di alimento) come accessori. Il rendimento organico è dato da:

₀ =

dove:

L_u è il lavoro utile;

L è il lavoro fornito dal fluido motore.

Mezzi per aumentare il rendimento del ciclo di Rankine

Dalla definizione di rendimento globale di un impianto:

_g = = _b = _{b u} = _{b o}

si deduce che il consumo di combustibile è, a parità di potenza utile dell'impianto, tanto più basso quanto più alto è il suo rendimento globale. Si comprende pertanto l'importanza economica di un elevato rendimento dell'impianto.

Fra i rendimenti parziali, fattori di _g, il rendimento del ciclo è quello che di solito assume i valori più modesti poichè riguarda la conversione di calore in lavoro.

Aumentare significa, a parità di Q₁, ridurre il calore Q₂ da sottrarre al fluido:

= 1 -

Sotto il profilo tecnico ed economico la possibilità di ridurre Q₂ corrisponde a ridurre la portata di fluido refrigerante, ad avere minori dimensioni del condensatore, con minori opere di costruzione iniziale, minore consumo di energia elettrica per azionare le pompe. Gli accorgimenti adottati, applicati o meno contemporaneamente, ad un impianto per aumentare sono:

a) aumento della pressione di vaporizzazione;

b) aumento della temperatura di surriscaldamento

c) surriscaldamenti ripetuti;

d) diminuzione della pressione di condensazione;

e) rigenerazione.

Normalmente gli accorgimenti a) e b) sono adottati contemporanemente per ridurre l'inconveniente del titolo di vapore troppo ridotto allo scarico della turbina.

figura 10.5

'= 1 - = 1 - 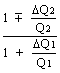= 1 - > = 1- < 1

Avere pressioni e temperature elevate comporta maggior costo iniziale e difficoltà costruttive. Il valore della massima temperatura di surriscaldamento del vapore è limitato dalla resistenza meccanica degli acciai che si devono adottare per i tubi del surriscaldatore e per le prime corone di palette delle turbine.

c)

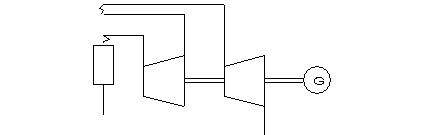
figura 10.6

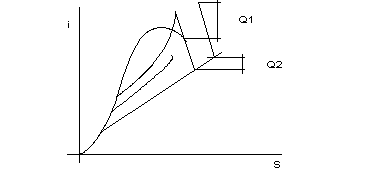
figura 10.7

'= 1 - >

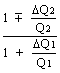Si verifica:

Se il titolo del vapore allo scambio termico è elevato le temperature di surriscaldamento sono accettabili. Siccome l'impianto risulta più complesso questo accorgimento è utilizzato per impianti con P_u 80 MW.

d) Nell'impianto motore termico dopo l'espansione del fluido in turbina occorre riportare il fluido alla pressione iniziale, per poter ripetere il ciclo.

Uno dei vantaggi dell'impiego di un fluido facilmente condensabile è che una volta ridotto allo stato liquido il fluido richiede un lavoro di compressione estremamente modesto o addirittura trascurabile rispetto la lavoro che si può ottenere quando esso, mediante fornitura di calore, è portato allo stato aeriforme. La fase di sottrazione di calore Q₂ coincide quindi con il cambiamento di stato del fluido, realizzato nel condensatore.

Dal punto di vista termodinamico un abbassamento della pressione di condensazione corrisponde a quanto rappresentato in figura 10.8:

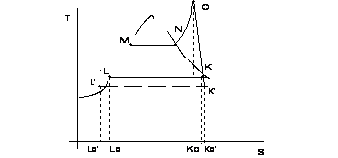
figura 10.8

Con riferimento alla figura 10.8:

Q₁ L₀'L'LL₀

Q₂ L₀LKK₀ - L₀'L'K'K₀'

'= 1 - >

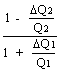Inoltre il lavoro del ciclo aumenta della quantità:

L = Q₁ + Q₂ Q₁

e) Vediamo l'effetto della rigenerazione.

Un modo per aumentare il rendimento del ciclo di Rankine è quello di scambiare calore fra il

vapore che si espande e l'acqua che deve esssere riscaldata dalla temperatura di condensazione a quella di vaporizzazione.

Riferiamoci al ciclo limite di Rankine a vapore saturo. Si fa avvenire l'espansione, anzichè secondo l'adiabatica isoentropica NK, secondo la NK'isoadiabatica con la LM:

figura 10.9

Se il calore (area K₀'K'NK₀ = L₀LMM₀) è utilizzato per preriscaldare l'acqua da T_L a T_M, il rendimento del ciclo limite diventerebbe:

'_l = 1 - = 1 - = 1 -

cioè diventerebbe uguale al rendimento del ciclo di Carnot HMNK fra le stesse temperature estreme T_L e T_M.

Per un ciclo reale con surriscaldamento, eliminando la fase di riscaldamento del liquido in caldaia e trasferendo con continuità il calore K₀'K'OKK₀ = L₀LMM₀ dal vapore che si espande all'acqua che deve essere scaldata, si otterrebbe un ciclo (LMNOK') con più alto rendimento.

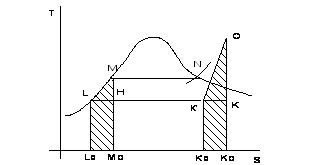
figura 10.10

Questa rigenerazione continua non si riesce a realizzarla in pratica a causa dell'impossibiltà pratica di scambio termico tra acqua e vapore che si espande; inoltre il titolo del vapore è troppo basso in turbina. La rigenerazione in pratica è effettuata con una tecnica differente: si "spilla" una parte del vapore circolante e si utilizza tutto il calore che può essere ceduto per il preriscaldamento dell'acqua.

Si può dimostrare che: '>

figura 10.11

Sono destinati alla produzione del vapore (a scopo industriale o di riscaldamento urbano) con una produzione congiunta di energia elettrica. Nelle industrie che richiedono forti quantità di vapore per i loro processi di produzione (industria chimica, tessile, alimentare, ecc.) oppure nei grossi impianti di riscaldamento urbano centralizzato conviene generare il vapore a temperature e pressioni più elevate di quelle richieste per l'utilizzazione termica e sfruttare l'espansione in una turbina, per ottenere la produzione di energia elettrica destinate ai fabbisogni dello stabilimento.

Impianto di recupero totale

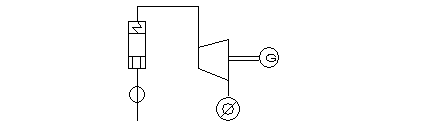
figura 10.12

Tutta la portata m che si espande in turbina viene inviata alla utenza termica. Il rendimento utile dell'impianto risulta:

_u = = = ₀

dove Q₁ - Q₂ è la potenza termica spesa in più per ottnere P_u.

Impianto a recupero parziale

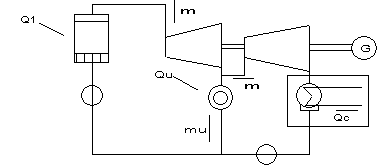
figura 10.13

La portata di vapore necessaria per l'utilizzazione termica viene estratta dalla turbina alla pressione richiesta, la restante portata continua ad espandersi e si scarica in un condensatore. Il rendimento utile risulta: _u =

Per la regolazione degli impianti di turbine a vapore si applicano le metodologie viste per la regolazione delle macchine "turbine":

- laminazione;

- parzializzazione.

Altri metodi sono usati in particolari applicazioni, come navi con impianto di turbine a vapore.

10.2 Impianti di turbine a gas

Il più semplice ciclo di funzionamento della turbina (apressione costante) è così costituito:

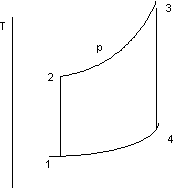
figura 10.14 a

figura 10.14 b

Con riferimento alle figure 10.14 a e b:

1-2 compressione;

2-3 riscaldamento a pressione costante;

3-4 espansione.

giunti al punto 4 si possono avere due casi:

- ciclo chiuso 4-1 raffreddamento del gas;

- ciclo aperto m₄ viene scaricato all'ambiente e viene sostituito m₁ da una massa d'aria  alla temperatura T₁: agli effetti termodinamici tutto accade come se lo stesso gas fosse stato raffreddato da 4 a 1.

Nel caso ordinario in 1 abbiamo solo aria perchè il combustibile verrà iniettato nella camera di combustione a partire dal punto 2.

Quindi la massa cambia durante il ciclo.

In figura 10.15 è riportato lo schema dell'impianto nel caso di ciclo aperto:

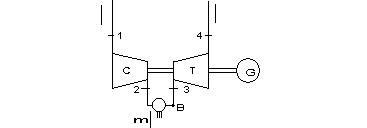
figura 10.15

Con riferimento alla figura 10.15:

- compressore C;

- combustore B;

- turbocompressore T.

Per ottenere l'equivalente ciclo chiuso il combustore B viene sostituito da uno scambiatore di calore tra 4 e 1 si inserisce un refrigeratore.

Rendimento del ciclo (Joule o Brayton)

_id = 1 - = 1 - = 1 - = 1 -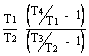

ma:

=

= =

= =

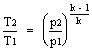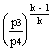_id = 1 - = 1 - f(T₃)

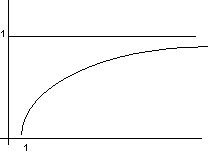
figura 10.16

Lavoro masico ideale

Dall'espressione:

_id =

L = _id c_p (T₃ - T₂)

si ha un massimo per L dato da:

L = L_t - L_c = c_p (T₃ - T₄) - c_p (T₂ - T₁) = c_p (T₃ + T₁) - c_p (T₂ + T₄)

da cui si deduce che L_max si ha per (T₂ + T₄)_min; ma T₁T₃ = T₂T₄ = cost e quindi T₂ = T₄.

figura 10.17

_lim =

_maxL = = =

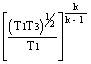L = L_t - L_c = c_p T₃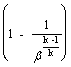 - c_p T₁

L = f (T₃, T₁, )

figura 10.18

Ciclo reale di turbina a gas

figura 10.19

Con riferimento alla figura 10.19:

Q₁ area 2₀233_0;

Q₂ area 1₀144_0;

L_i = Q₁ - Q₂ area 1234 del ciclo.

Si ha inoltre:

figura 10.20

_g =

figura 10.21

Nel campo di interesse pratico _g cresce sempre con T3.

Pratiche attuate per migliorare il ciclo semplice

Queste tecniche possono essere raggruppate nelle seguenti:

a) compressione interrefrigerata;

b) ricombustione;

c) rigenerazione;

d) rigenerazione più compressione interrefrigerante;

e) rigenerazione più ricombustione.

Con le tecniche a) e b) il rendimento risulta inferiore al caso ideale, ma aumenta L_i.

Con la tecnica c) aumenta il rendimento ma non il lavoro massico. Si ha una efficace rigenerazione data dal rapporto tra il calore effettivamente scambiato e il calore massimo scambiabile: R_s =

Con le tecniche d) e e) aumenta il rendimento ed il lavoro massico.

[Figure su foglio a parte]

figura 10.22 - ciclo con compressione interefrigerante

figura 10.23 - ciclo con combustioni o riscaldamenti ripetuti

figura 10.24 - ciclo a compressione interefrigerata ed espansione interriscaldata

figura 10.25 - ciclo ideale a rigenerazione totale

figura 10.26 - ciclo con riscaldamenti o combustioni intermedi e rigenerazione

figura 10.27 - ciclo rigenerativo con refrigerazioni e riscaldamenti intermedi

figura 10.28 - ciclo con refrigerazioni intermedie e rigenerazione

Vediamo ora un esempio di utilizzazione della caratteristica manometrica del turbocompressore.

A) Punto di funzionamento

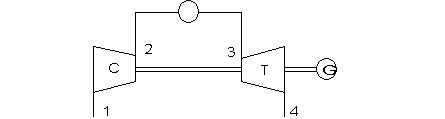
figura 10.29

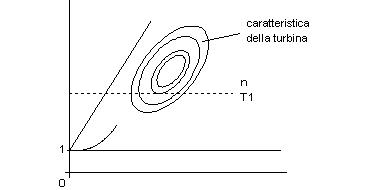
figura 10.30

Per il turboespansore:

m_a + m_b = m_a

p₄ = p₁

p₃ = _b p₂ = _b p₁

Se lavoriamo a T₃ costante: m_a p₁ f(k,,p₁)

nel campo di turbina critica: m_a p₁

Se si regola l'impianto per laminazione all'aspirazione del compressore:

figura 10.31a

figura 10.31b

Il compressore rimane costante. Il rapporto critico della turbina vale:

m 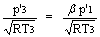= cost

deve verificarsi: _{cr t} p₁ = '_{cr t} p'₁

'_{cr t} = _{cr t}

figura 10.32

Il punto di funzionamento del gruppo rimane invariato finchè la turbina lavora in campo critico.

B) Impianto di TG bialbero

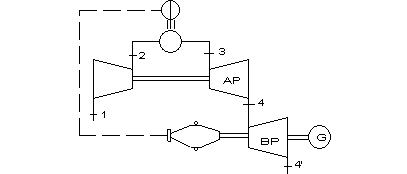
figura 10.33

La turbina AP comanda il turbocompressore mentre la turbina BP aziona l'utenza meccanica.

AP generatore di gas;

BP turbina di potenza.

In condizioni di equilibrio devono essere soddisfatte le condizioni:

equilibrio meccanico generatore di gas

P_{a compressore} = P_uAP

dove: L_cis = c_p T₁

L_tis = c_p'T₃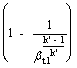

dove: k= aria;

k'= gas combusti.

Introducendo la dosatura = :

c_pT₁ = _{c t mc mt} c'_p T₃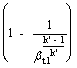

posso ad esempio determinare _t1 per l'equilibrio noti gli altri valori.

_{c b} = _{t1 t2}

Continuità tra la turbina AP e turbina BP

m_AP = m_BP

dove:

m_AP = m + m_b

Se suppoiniamo critiche entrambe le turbine:

m_AP = K'A' = K''A''

Equazione della conservazione della quantità di moto

Viene sostituita con una linea di evoluzione politropica.

_yt = =

da cui:

=

Sapendo che Q_e = 0: L_i = - i - E_c

Inotre considerando E_c 0:

Li + Lw = -

= t1 =

Dalla continuità:

=

da cui uguagliando le due espressioni, si ottiene:

= = cost.

da cui, cosiderando _yt costante:

= cost

C) Punto di funzionamento di una turbopompa

figura 10.34

Applichiamo il I principio per determinare il lavoro per unità di massa che occorre fornire per portare l'acqua dal serbatoio di livello a al serbatoio di livello b.

L_i = g(z_b - z_a) + + + L_wp + g Y_c

L_i = g + L_wp + g Y_c

dove Y_c sono le perdite che si hanno complessivamente nei condotti.

Definiamo la prevalenza totale:

H_t =

Per un circuito aperto H_t z_b - z_a = H_g prevalenza geodetica.

Applicando il I principio tra l'ingresso 1 e la mandata 2 della turbopompa:

L_i = g(z₂ - z₁) + + + L_wp = g + L_wp

dove Hu = è la prevalenza manometrica.

Uguagliando le due espressioni di L_i: H_u = H_t + Y_c

dove il primo membro rappresenta la caratteristica interna, mentre il secondo membro rappresenta la caratteristica esterna.

La caratteristica interna di una turbopompa è del tipo:

figura 10.35

m = Q dove Q è la portata in volume.

La caratteristica esterna: H_t + Y_c = H_g + Q²

Per moto turbolento: Y W₂

dove W₂ è la velocità dell'acqua nel condotto

Per due pompe sistemate in serie:

figura 10.36a

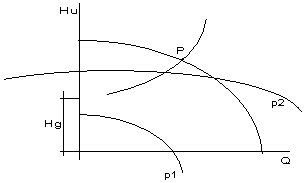
figura 10.36b

La prevalenza complessiva è la somma delle prevalenze per ogni valore della portata.

Per due pompe sistemate in parallelo:

figura 10.37a

Se le due pompe sono identiche ed hanno caratteristiche manometriche senza massimi (a parità di H_u sommo Q):

figura 10.37b

Se le due pompe hanno caratteristiche distinte sempre senza massimi:

figura 10.37c

si possono avere condizioni di portata negativa in una della pompe.

---