PROFILI LAMINARI (sesta serie)

tecnica

PROFILI LAMINARI (sesta serie)

La nomenclatura dei profili laminari è del tipo rs_x-tvv, a=y (per esempio 63₂-215, a=0.5), dove la prima cifra r indica la serie laminare, la seconda cifra s indica la posizione, in decimi della corda, del picco di espansi 959f53j one sul profilo base all'angolo a_z.l., il pedice x rappresenta la semiestensione della sacca laminare, la cifra t indica in decimi il C_li, il gruppo vv indica lo spessore massimo percentuale, ed infine il gruppo a=y indica il tipo di linea media essendo y la lunghezza del tratto lungo il quale la linea media ha carico costante all'incidenza ideale (se è a=1 la linea media si omette).

La forma di un profilo laminare si sviluppa a partire dal profilo base, che fornisce la distribuzione di spessori, e dalla linea media le cui ordinate vanno opportunamente scalate di un fattore pari proprio al C_li della linea media del profilo che bisogna realizzare. Se, ad esempio si vuole realizzare il profilo 63₂-215 a=0.5, occorre partire dal profilo base 63₂-015 ed accoppiare a questo la linea media a=0.4 con le ordinate opportunamente moltiplicate per il valore 0.2.

La geometria dei profili laminari non è esprimibile, come quella dei profili NACA a quattro e cinque cifre, da una relazione analitica essendo invece definita in forma tabulare relativamente ad un numero limitato di punti. Di conseguenza, al fine di poter descrivere in maniera adeguata la forma di un profilo laminare, si rende necessaria un'interpolazione tra i diversi punti noti del profilo stesso. Detta interpolazione si esegue con una spline cubica ovvero con una curva del terzo ordine che soddisfi a precise condizioni di continuità. In particolare, se diciamo y_i(x) la curva interpolante tra i punti e , dovranno risultare verificate le relazioni

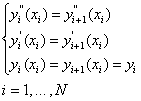
essendo N  il numero dei punti di tabulazione.

A questo punto vediamo come si determinano dette curve. Anzitutto osserviamo che, dovendo essere y_i(x) una cubica, la sua derivata seconda sarà una retta che, per i requisiti di continuità sopra precisati, dovrà passare per i punti e , ovvero si avrà:

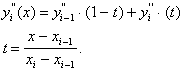
Integrando, quindi, due volte questa espressione ed imponendo la continuità della y si ottiene l'equazione della iesima curva interpolante in funzione dei coefficienti incogniti :

con

Imponendo, infine, la continuità della derivata prima si ha:

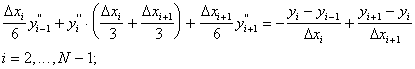
ovvero si ha un sistema di N-2 equazioni nelle N incognite che può essere risolto in forma chiusa una volta imposte le condizioni agli estremi e . Risolto il sistema e noti pertanto gli N coefficienti , risulteranno definite le equazioni delle curve interpolanti secondo l'espressione sopra definita.

Si riportano nelle pagine seguenti il plot del profilo NACA 63-206 ed i relativi andamenti delle coordinate parametriche.