5.1.1 Conservazione della massa

Sia m(t) la massa di fluido in _c all'istante t e m(t + t) = m(t) + m la massa di fluido in in all'istante t + t. Indicando con m_f1 la massa che entra e con m_f2 la massa di fluido che esce dalla regione nell'intervallo di tempo t è, per la conservazione della massa: m = mc + mf2 - mf1 = 0

dividendo per t e passando al limite per t 0 si ha, tenendo conto che il vettore di superficie è (fig. 5.1) orientato verso l'esterno:

Figura 5. 1

Attraverso i confini individuati dalla superficie A_c - (A₁ + A₂) non si hanno trasferimenti di massa, ma solo di calore Q_c e di lavoro L_i (per mezzo di albero rotante) e quindi si ottiene:

e quindi:

che nel caso di moto stazionario si semplifica in:

espressione che prende il nome di equazione di continuità e dice che il flusso netto di massa rimane costante e quindi non ci sono accumuli di liquido.

Ora seguiamo lo stesso procedimento per la quantità di moto.

dividendo per t e passando al limite per t 0 si ha :

ed essendo:

in quanto attraverso la superficie Ac - (A₁ + A₂) non si ha trasferimento di massa, si ottiene:

che in condizioni stazionarie si semplifica in:

comprende:

- la forza che complessivamente le pareti solide esercitano sul fluido per reazione alle forze di pressione e di attrito trasmesse dal fluido;

- la risultante delle forze di pressione (positive nella direzione del moto) trasmesse al sistema in A₁ ed A₂ dal fluido contiguo. Essendo orientato verso l'esterno, essa è pari a:

- la risultante delle forze di attrito trasmesse al sistema in A₁ e A₂ dal fluido contiguo. Questa è in genere trascurabile rispetto alle altre;

- la risultante delle forze di gravità (peso del sistema) pari a:

dove è il peso per unità di volume.

Otteniamo quindi l'espressione:

Se il moto è unidimensionale oltre che stazionario e se il peso è trascurabile, come in genere è per i fluidi comprimibili, si ottiene l'espressione semplificata

- p₁ A₁- p₂ A₂ = ₂ c₂ cos₂ A₂ + ₁ c₁ cos₁ A₁

dove ₁ e ₂ sono gli angoli che le velocità formano con i versori normali alle sezioni A₁ e A₂ ed essendo per l'equazione di continuità:

₁ c₁ cos₁ A₁ = ₂ c₂ cos₂ A₂ = m

si ha:

- p₁ A₁ - p₂ A₂ = m( - )

Il momento risultante M_O rispetto ad un punto fisso O, in un sistema di riferimento inerziale, delle forze esterne applicate ad un sistema è dato da:

dove è il momento della quantità di moto del sistema rispetto al punto O.

Con riferimento al sistema di massa m compreso nell'istante t nel volume _c, indichiamo con il raggio vettore, dal punto O, di un elemento dV del volume di controllo _c si ottiene, in condizioni stazionarie:

Perlopiù nelle applicazioni si considera il momento assiale M_a rispetto ad un asse fisso, in un sistema di riferimento inerziale, delle forze applicate al sistema fluido dall'esterno. Indicando con c_u la componente tangenziale, in un piano normale all'asse aa (vedi figura 5.2), della velocità di un elemento fluido distante r dall'asse aa, il momento Ma rispetto a tale asse è:

Ma =

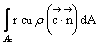
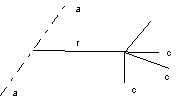
Figura 5. 2

Se il moto è unidimensionale oltre che stazionario l'espressione si semplifica diventando.

Ma = r₂ c_{u2 2} cos₂ A₂ + r₁ c_{u1 1} cos₁ A₁

e tenedo conto dell'equazione di continuità:

Ma = m (r₂ c_u2 - r₁ c_u1)

Energia

La conservazione dell'energia di un sistema fluido scritto in forma euleriana assume la forma:

Q_e + L = lim

t0

dove:

L = L_i -

Elaborando il termine nell'integrale:

La variazione complessiva di energia del sistema vale:

E= E (t + t) -E (t) = E_c (t + t) + E_f2 - E_f1 - E(t)

indicando con E la somma dei termini:

E = U + + gz

il limte si esprime con:

e quindi:

Q_e + L_i =

con:

E_f = E + pv = i + + gz

in condizioni stazionarie ( ) si ha:

Q_e + L_i =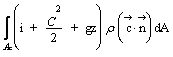

e se il moto è unidimensionale, oltre che stazionario:

Q_e + L_i = m [ i₂ - i₁ + + g (z₂ -z₁)]

Per quanto riguarda il II principio della termodinamica di solito nelle applicazioni ci interessa la differenza di entropia fra le sezioni A₁ e A₂ attraversate da una corrente fluida in moto stazionario ed unidimensionale. Tale differenza si determina, per un gas perfetto, integrando la:

dS = c_p

fra gli stati che si hanno nelle sezioni suddette:

S₂ - S₁ = c_pln

per il vapore i valori di S₂ e S₁ dell'entropia si leggono sul diagramma di Mollier in corrispondenza dei punti che rappresentano lo stato nelle sezioni A₁ e A₂.

Consideriamo una turbina semplice caratterizzata da una corona di palette che delimitano con lo statore, in cui sono infisse, tanti condotti di forma opportuna (distributore) nei quali il fluido si espande, e da una corona di palette che, solidali con il rotore, delimitano con l'involucro esterno una serie di condotti mobili (girante). Questi fronteggiano i condotti fissi con opportuna orientazione, raccogliendo lavoro dal fluido scaricato dal distributore ad elevata velocità. Nella girante il fluido può subire o meno una ulteriore espansione.

condizioni:

ingresso distributore 0;

uscita distributore/ingresso girante 1;

uscita girante 2.

Portate in massa fluido motore

m = ₁ A₁ c_a1 = ₂ A₂ c_a2

dove: A₁ = ₁ d₁ l₁

A₂ = ₂ d₂ l₂

in genere d = d₁ = d₂ con :

d: diametro medio della palettatura mobile;

l₁: altezza della palettatura all'ingresso;

l₂: altezza palettatura all'uscita della girante;

₁, ₂: coefficenti di ingombro che tengono conto dell'influenza dello spessore delle palette.

Triangoli delle velocità

Per lo studio delle turbomacchine col metodo unidimensionale si utilizzano i triangoli dei vettori all'ingresso e dei condotti mobili.

sono le velocità del fluido relative alla girante, mentre sono le velocità periferiche della girante ai raggi medi r₁ e r₂.

Le velocità assolute, relative e periferiche (trascinamento) sono legate dalla relazione:

La rappresentazione consueta dei triangoli di velocità è del tipo:

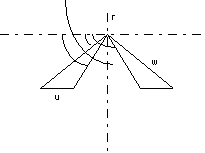
Figura 5. 3

₁ = angolo della velocità assoluta in ingresso;

₂ = angolo della velocità relativa in ingresso;

₁ = angolo della velocità assoluta in uscita;

₂ = angolo della velocità relativa in uscita.

Per la turbina assiale è in genere u₁ = u₂ e la retta rr rappresenta la direzione assiale.

Coppia motrice

Per la determinazione della coppia motrice applichiamo l'espressione:

Ma = m(r₂c_u2 - r₁c_u1)

fra le sezioni di ingresso e di uscita della girante considerando come asse aa quello di rotazione dell'albero. Le forze di pressione trasmesse in A₁ e A₂ hanno momento nullo rispetto all'asse di rotazione; analogamente le forze di gravità. Pertanto Ma è pari alla somma dei momenti impressi al fluido dalla girante e dalla superficie dello statore che delimita i condotti mobili. Il contributo di quest'ultima è in genere tracurabile e quindi la coppia motrice (uguale ed opposta alla coppia impressa dalla girante al fluido) è data da:

c = m(c_u1 r₁ - c_u2r₂)

Lavoro massico interno

La potenza P_i che la girante riceve dal fluido è, indicando con la sua velocità angolare:

P_i = c = m(r₁c_u1 - r₂ c_u2) = m(u₁c_u1 - u₂c_u2)

ed il lavoro massico interno Li è dato da:

L_i = = u₁c_u1 - u₂c_u2

e per la turbina assiale diventa, per u₁ = u₂ = u:

L_i = u (c_u1 - c_u2)

E'utile ricavare una diversa espressione di L_i dall'equazione dell'energia applicata ad una turbina (nella conversione che considera positivo il lavoro fatto dal fluido sulla macchina): Q_e - L_i = i + E_c + ...

Il flusso può essere considerato adiabatico (Q_e = 0) a meno che le palette non siano refrigerate, in quanto il calore trasmesso all'esterno è trascurabile rispetto alle variazioni di energia che il fluido subisce nella macchina.

Si ha pertanto: L_i = - i - E_c - ...

Applicata al distributore (0 - 1) si ottiene:

-i₀₁= E_c01 =

che scritta per la girante (1 - 2) nel moto ad essa relativo si ha:

i₁₂ + E_cr12 + E_cf12 = 0

dove:

E_cr12 =

rappresenta la variazione di energia dovuta al campo di forze centrifughe.

La caduta di entalpia nella girante vale:

i₁₂ =

applicandola fra le sezioni di uscita e di ingresso nella turbina (0 - 2) si ha:

L_i = -i₀₁ - i₁₂ - E_c =

Applicando il teorema ci Carnot ai triangoli di velocità:

w1² = c1² + u1² - 2 c1 u1 cos1 = c1² + u1² - 2 u1 cu1

w2² = c2² + u2² - 2 c1 u1 cos2= c2² + u2² - 2 u2 cu2

e sottraendo membro a membro:

u1 cu1 - u2 cu2 =

coincidente con l'espressione di Li ricavata mediante la relazione della coppia motrice.