|
|
| |
MOTO VARIO NELLE CONDOTTE IN PRESSIONE
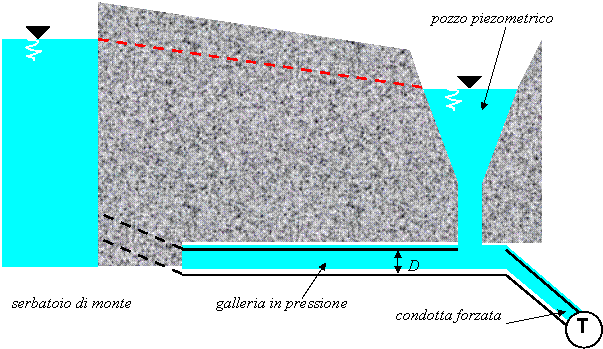
L'impianto in figura consta di una galleria in pressione, di un pozzo piezometrico e di una condotta forzata, che, sfruttando l'energia cinetica dell'acqua, con una turbina posta all'estremità, produce corrente elettrica.
Quando l'otturatore della turbina viene chiuso, con un tempo pressoché istantaneo, nella condotta forzata vengono a formarsi oscillazioni elastiche o di pressione che si propagano fino all'imbocco della condotta. Esse si esauriscono in un tempo pressoché uguale alla manovra di apertura dell'otturatore. La portata d'acqua che dal serbatoio continua a defluire verso la condotta urta istantaneamente contro la massa d'acqua ferma nella condotta. L'acqua in eccesso viene ad alimentare il pozzo piezometrico, che funge quindi da polmone per l'impianto. Nella galleria in pressione vengono quindi a formarsi onde di massa, di una durata molto maggiore rispetto a quelle elastiche. Sono spostamenti rigidi di massa tra il pozzo piezometrico e il serbatoio di monte e continuano finchè tutta l'energia cinetica dell'acqua che defluisce dal serbatoio, non viene dissipata dalle resistenze idrauliche.
OSCILLAZIONI DI MASSA: per lo studio delle oscillazioni di massa adoperiamo l'equazione indefinita di continuità per le correnti i) e l'equazione del moto ii):
![]() i)
i)
![]() ii)
ii)
Dalla prima si deduce che ![]() , mentre dalla seconda.
, mentre dalla seconda.
Introducendo la formula di Darcy-Weisebach nella i) e integrando lungo la galleria in pressione, abbiamo:
![]() iii)
iii)
Dall'equazione di continuità sappiamo pure che: ![]() , da cui si ricava :
, da cui si ricava :
![]() iv)
iv)
Introducendo la iv) nella iii) si ottiene:
![]() v)
v)
La v) non è direttamente risolvibile per via analitica, se non sfruttando il metodo delle differenze finite. Il termini mediano rappresenta le resistenze idrauliche, sempre opposte al verso del moto.
Ipotizzandole nulle (in prima approssimazione) si ottiene un'equazione differenziale del sercond'ordine del tipo:
![]() vi)
vi)
Imponendo che ![]() allora la vi) fornisce
la soluzione esatta:
allora la vi) fornisce
la soluzione esatta:
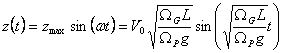 vii)
vii)
La vii) rappresenta la funzione delle oscillazioni di massa che si verificano nella galleria in pressione.
OSCILLAZIONI ELASTICHE (O DI PRESSIONE):
Per studiare questo tipo di oscillazioni, ci rifacciamo alla definizione di celerità, ossia la rapidità di propagazione di una perturbazione in una definita direzione s; in particolare, possiamo, definire:
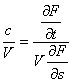
con F la funzione F=F(s,t) che descrive la perturbazione; la celerità, definita come ds/dt, per le condotte in questione si aggira intono ai 1000 m/s, per cui dal rapporto summenzionato possiamo vedere che
![]() viii)
viii)
Ora, per studiare le oscillazioni perturbatrici, poniamo, in via iniziale, alcune approssimazioni:
![]() ; ix)
; ix)
![]() ;
;
Se scriviamo l'equazione del moto possiamo vedere che:
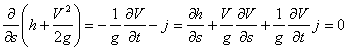 x)
x)
In virtù della viii) e della ix), la x) si riscrive:
![]() xi)
xi)
Che viene definita come l'Equazione del moto delle onde elastiche.
Dall'equazione i) di continuità delle correnti, possiamo dedurre:
![]()
che, in virtù delle considerazioni dianzi dette e delle ipotesi introduttive, si riscrive come:
![]() xii)
xii)
La xii) può essere espressa in termini di ![]() e di E (per la formula
di Mariotte), essendo rispettivamente, il modulo di comprimibilità del fluido
ed il modulo di elasticità della condotta, supposto che essa sia costruita con
un materiale a comportamento elastico/lineare.
e di E (per la formula
di Mariotte), essendo rispettivamente, il modulo di comprimibilità del fluido
ed il modulo di elasticità della condotta, supposto che essa sia costruita con
un materiale a comportamento elastico/lineare.
Possiamo allora riscrivere la xii) nella xiii):
![]() xiii)
xiii)
dove D ed s sono rispettivamente diametro e spessore della del condotto; e quindi, semplificando, si perviene all'Equazione indefinita di continuità:
![]() xiv)
xiv)
il termine 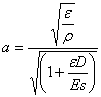 è la celerità con cui
si propagano le onde elastiche. Riassumendo le due equazioni che descrivono
l'andamento delle oscillazioni elastiche sono:
è la celerità con cui
si propagano le onde elastiche. Riassumendo le due equazioni che descrivono
l'andamento delle oscillazioni elastiche sono:
EQUAZIONE DEL MOTO: ![]() xv)
xv)
EQUAZIONE DI CONTINUITA': ![]() xvi)
xvi)
In realtà, quando trattiamo con onde elastiche, analizziamo quella parte dell'impianto che soggiace al pozzo piezometrico, ovvero la condotta forzata. Essa, per quanto corta possibile, presenta velocità di deflusso assai trascurabili, che inducono un carico cinetico irrisorio rispetto al carico piezometrico. Percui, in detta zona dell'impianto, H è approssimabile ad h. Inoltre è opportuno cambiare il sistema di riferimento: invece di scegliere un sistema di ascisse nel verso del moto dell'acqua defluente inizialmente, poniamo un riferimento x uscente dall'otturatore e diretto verso il serbatoio.
In questo caso si ha ![]() , ove K è una costante arbitraria. Ne consegue che
, ove K è una costante arbitraria. Ne consegue che ![]() . Operando un cambiamento di variabili nelle equazioni del
moto e di continuità, le xv) e xvi) divengono:
. Operando un cambiamento di variabili nelle equazioni del
moto e di continuità, le xv) e xvi) divengono:
![]() xvii)
xvii)
![]() xviii)
xviii)
Derivando la prima in x e la seconda in t, otteniamo un'unica equazione differenziale del second'ordine che sublima il sistema di equazioni differenziali fornito dalle xii) e xiii), e cioè:
![]() xix)
xix)
La xix) trova soluzione mediante la risoluzione con il Principio
di D'Alambert (o delle corde vibranti), che porge le due funzioni F e ![]() ;
;
![]() xx)
xx)
![]() xxi)
xxi)
Nelle xx) e xxi) ![]() rappresentano due
funzioni proprie che descrivono il colpo d'ariete e l'andamento delle
oscillazioni elastiche nella condotta forzata. In particolare, entrambi sono
nulle se si effettua manovra alcuna sull'otturatore; F è non nulla quando
l'otturatore viene chiuso o parzialmente chiuso e
rappresentano due
funzioni proprie che descrivono il colpo d'ariete e l'andamento delle
oscillazioni elastiche nella condotta forzata. In particolare, entrambi sono
nulle se si effettua manovra alcuna sull'otturatore; F è non nulla quando
l'otturatore viene chiuso o parzialmente chiuso e ![]() è non nulla dal
momento che le onde elastiche hanno raggiunto l'imbocco dell'otturatore.
Entrambe si muovono con celerità, rispettivamente,
è non nulla dal
momento che le onde elastiche hanno raggiunto l'imbocco dell'otturatore.
Entrambe si muovono con celerità, rispettivamente, ![]() e
e ![]() .
.
Ognuna di queste funzioni è caratterizzata da un periodo, o
meglio, da una durata di fase, che chiameremo ![]() , e che indicheremo come:
, e che indicheremo come:
![]() xxii)
xxii)
In sostanza, ![]() indica la durata che
una funzione, tra le due, impiega a ritornare al proprio valore iniziale, ed è
quindi plausibile affermare che se:
indica la durata che
una funzione, tra le due, impiega a ritornare al proprio valore iniziale, ed è
quindi plausibile affermare che se:
![]() manovra lenta
manovra lenta
![]() manovra
veloce.
manovra
veloce.
Lo studio dell'andamento delle pressioni e sovrapressioni nelle condotte è dato dal tipo di manovra effettuata sull'otturatore. In particolare, per manovra velocissima, in prima approssimazione, istantanea, possiamo vedere che l'andamento delle oscillazioni è causato da:
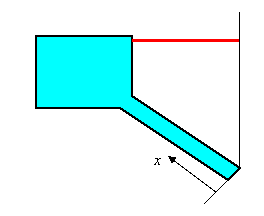
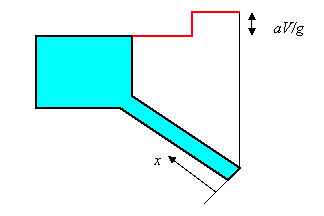
In questa manovra, l'otturatore è chiuso Qui, l'otturatore ha subito una manovra istantanea e il carico totale subisce un sovraccarico pari ad aV/g;
![]()
Questo
andamento si ripete a periodi di ![]() e dopo 2
e dopo 2![]() esso riacquista la posizione iniziale, ovvero, nel grafico:
esso riacquista la posizione iniziale, ovvero, nel grafico: 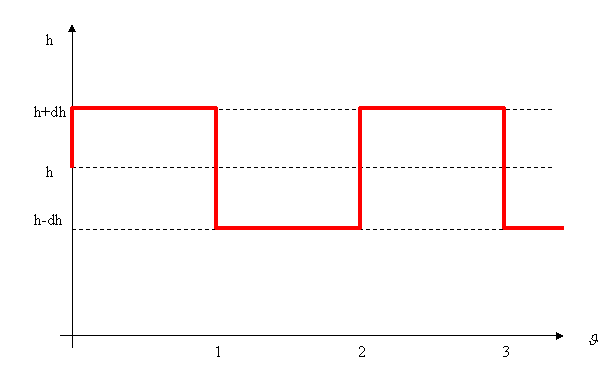
Analogamente possiamo fare per una manovra, seppur brusca, ma non istantanea. In particolare, riportiamo qui la situazione in cui la manovra sia già stata effettuata e che siano in atto oscillazioni di tipo F:
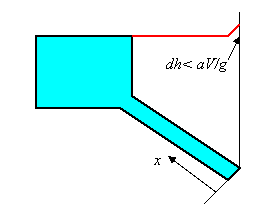
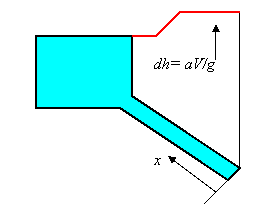
Si può riportare su un grafico l'andamento del carico:
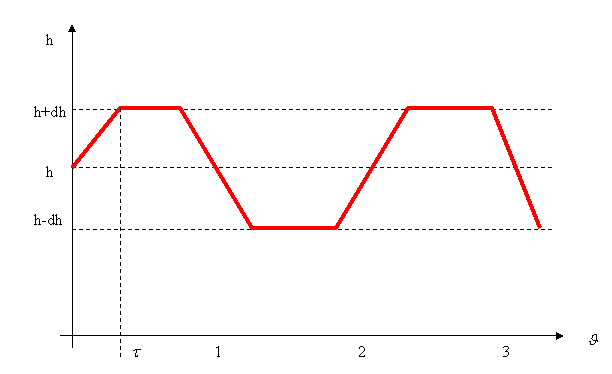
Ed in maniera analoga si può definire il grafico per una manovra
lenta, ossia per ![]() :
:
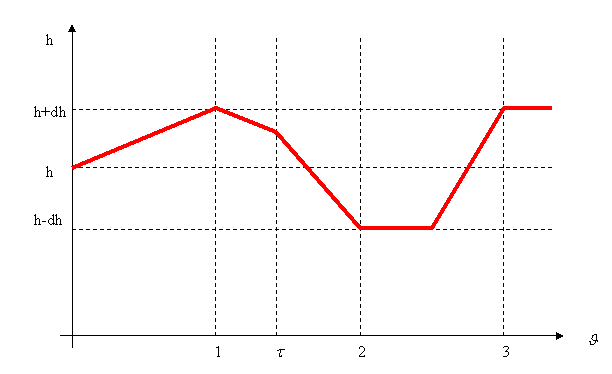
E' importante lo studio del sovraccarico. Oltre alle elevate pressioni che si registrano nella condotta forzata, è d'obbligo premunirsi contro le sovra-pressioni che possono provocare la crisi della sezione della condotta. Possiamo quindi utilizzare, nello studio delle pressioni, la nota formula di Mariotte:
![]()
CASSE D'ARIA
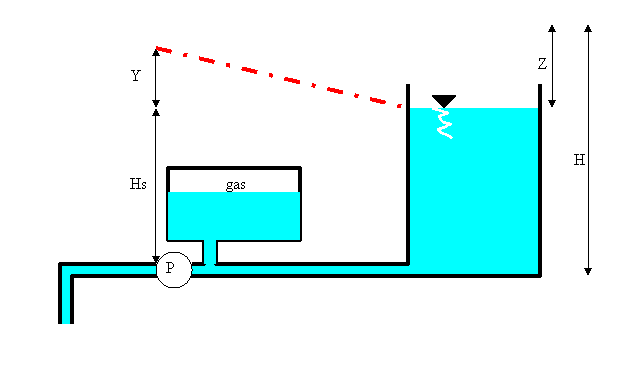
Invece di un impianto idroelettrico, si analizzi un impianto di pompaggio dell'acqua da un deposito a monte ad un serbatoio a valle, il cui pelo libero rimane ad un livello costante nel caso di un regime regolare. In un regime statico, corrisponde all'intera condotta un carico Hs, maggiorato, al punto di pompaggio, delle perdite concentrate e distribuite che il fluido incontra nel deflusso. Se istantaneamente viene operata una manovra sull'otturatore della pompa, il sistema, ed in particolare la condotta di mandata, è soggetto ad oscillazioni di massa, alle quali, parzialmente, sovviene la cassa d'aria posta subito a valle della pompa. In particolare, quando essa interrompe il pompaggio della portata nel condotto, la cassa d'aria libera nella tubazione fluido immagazzinato, lasciando il gas soprastante libero di espandersi e di diminuire la propria pressione interfacciale. In sostanza, le oscillazioni di massa sono presenti tra il serbatoio di valle e la cassa d'aria che, come abbiamo dianzi detto, cautela l'impianto di pompaggio dalle oscillazioni stesse. Ci interessa Z, ossia di quanto varia il carico effettivo del sistema e per farlo dobbiamo considerare le equazioni del moto xxiii), di continuità xxiv) e dello stato dei gas xxv):
![]() xxiii)
xxiii)
![]() xxiv)
xxiv)
![]() xxv)
xxv)
Nelle succitate formule, alfa e beta sono i fattori di perdita, rispettivamente distribuite e concentrate, V è il volume, n è un particolare esponente che dipende dal tipo di trasformazione che si sta considerando, ossia, n vale 1 se la trasformazione è isoterma, ovvero vale 1,4 se la trasformazione è adiabatica. Come noteremo, a favore della sicurezza, è opportuno scegliere sempre un fattore n di trasformazione adiabatica.
Poiché il sistema differenziale si può risolvere soltanto con il metodo delle differenze finite, è opportuno trasformare le variabili da dimensionali ad dimensionali, ovvero, ponendo:
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]() ;
;
Il sistema diviene allora, in virtù delle semplificazioni
suddette: ![]() .
.
L'equazione trovata fornisce, per ogni valore di u e di sigma, univocamente la z, e poiché, ai fini applicativi, ci serve solamente cautelarci dalle oscillazioni più intense, cioè quelle per le quali z=zmax e z=zmin, ci si riconduce ad un problema di massimi e di minimi. Inoltre, quando le oscillazioni avvengono per dette z, la velocità è nulla, per cui la quota z diviene funzione solamente di sigma, ed in particolare si trovano due soluzioni per l'equazione, a cui corrispondono una zmin (radice negativa) ed una zmax (radice positiva) e quindi, rispettivamente, una depressione ed una soprapressione.
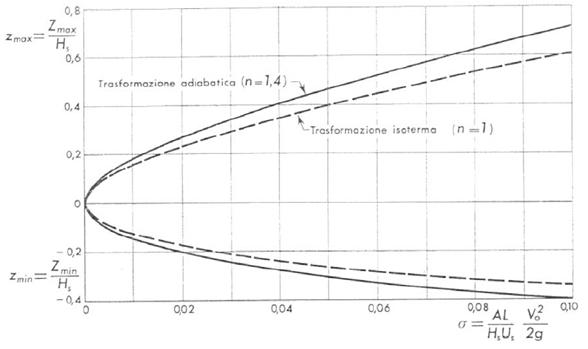
Come si può notare, per valori costanti di sigma, sono sempre
maggiori le soprapressioni che le depressioni, è questo per la lieve asimmetria
della funzione ![]() .
.
Il dimensionamento delle casse d'aria avviene considerando due
aspetti: ![]() e n; in primo luogo,
infatti, n lo scegliamo come 1,4; mentre
e n; in primo luogo,
infatti, n lo scegliamo come 1,4; mentre ![]() viene scelto in base
al tipo di strozzatura che viene adoperata. Ai fini pratici, la strozzatura è
quella che fornisce una perdita di carico, per una data velocità di moto
permanente, pari alla depressione zmin che registreremmo alla fine del processo
del moto vario e delle oscillazioni. In sostanza abbiamo che:
viene scelto in base
al tipo di strozzatura che viene adoperata. Ai fini pratici, la strozzatura è
quella che fornisce una perdita di carico, per una data velocità di moto
permanente, pari alla depressione zmin che registreremmo alla fine del processo
del moto vario e delle oscillazioni. In sostanza abbiamo che: ![]() ; Noto
; Noto ![]() si definisce zmax; una
volta definita essa, sul grafico sigma-z si registra zmin, dal quale è
immediato calcolarsi il volume della cassa d'aria, dalla formula:
si definisce zmax; una
volta definita essa, sul grafico sigma-z si registra zmin, dal quale è
immediato calcolarsi il volume della cassa d'aria, dalla formula:
![]() ed anche
ed anche 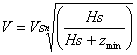
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025