In tale caso si utilizza un modello di previsione delle frequenze dei risultati che e' quello normale.

Nel seguito descriveremo alcuni modelli di previsione delle frequenze, gli ambiti di applicazione e come si stimano i parametri da cui essi eventualmente dipendono a partire da un numero limitato di ripetizioni dell'esperimento stocastico che intendiamo modellizzare.

Definizione di probabilita'

La frequenza prevista, definita a priori, dei risultati di un certo esperimento prende il nome di probabilita'. Ci chiediamo come assegnare tale probabilita'. Secondo una definizione classica, dovuta a Laplace, se un esperimento aleatorio da' luogo a N risultati elementari (non ulteriormente scomponibili) e se non c'e' alcun motivo per cui uno di questi si presenti piu' frequentemente degli altri, si assegna a ciascuno di essi una probabilita' paria a 1/N.

Ad esempio nel caso semplice del lancio della moneta, i risultati possibili sono 2 (testa e croce), se la moneta non e' truccata si assegna a ciascuno dei due risultati probabilita' pari a ½.

Si osservi come la probabilita' soddisfi esattamente alle stesse proprieta' cui soddisfa la frequenza relativa che si osserva ripetendo N volte l'esperimento. E' cioe' un numero positivo compreso tra 0 e 1 e la probabilita' che si verifichi o testa o croce (ovvero dell'insieme formato da testa e croce), che e' l'evento certo e' pari a 1, cosi' come la frequenza relativa dell'insieme contenete tutti i risultati dell'esperimento e' 1. La probabilita' che non si verifichi ne' testa ne' croce e' altresi' pari a zero; essa e' la probabilita' dell'insieme vuoto.

Una tale definizione di probabilita' non sempre e' applicabile. Cosa succede se la moneta e' truccata?

Esiste una definizione di probabilita' generale, dovuta a Kolmogorov. Si tratta di una definizione astratta e piu' complessa che presuppone la conoscenza dell'algebra degli insiemi e dalla teoria della misura.

Tale definizione si semplifica nel caso in cui l'esperimento stocastico presenta un numero finito e discreto di risultati. Ad esempio nel caso del lancio di un dado non truccato i possibili risultati sono 1, 2, 3, 4, 5, 6. Chiamiamo W l'insieme contenente tutti i risultati dell'esperimento,  W nell'esempio. Il singolo risultato si chiama evento semplice. Di ognuno di tali eventi vogliamo conoscere la probabilità. Ma vogliamo poter fare ben di più. Ad esempio dare le probabilità che esca un numero dispari. Una tale congettura sui risultati si traduce nell'insieme A = , che costituisce quello che chiamiamo un evento complesso; anche di questo vogliamo poter dare la probabilità. Si comprende come la probabilità vada definita per tutti i possibili eventi complessi. L'insieme di tutti gli eventi complessi lo chiamiamo A . Vogliamo altresì conoscere la probabilità di eventi complessi ottenuti dall'unione o dall'intersezione di altri eventi complessi, ne consegue che anche tali insiemi devono stare in A . Se l'insieme degli eventi elementari W è finito e discreto tale insieme A è quello che contiene tutti i sottoinsiemi di W A . Nel caso più generale si indicheranno le proprietà di tale insieme, che sono quelle che definiscono una sigma algebra di eventi. Individuato A o in maniera astratta definite le caratteristiche che esso deve possedere si può definire la probabilità, nuovamente in maniera astratta, come una funzione che ad ogni elemento di A fa corrispondere un numero reale compreso tra 0 e 1 che soddisfa alle proprietà assiomatiche (di una misura) seguenti:

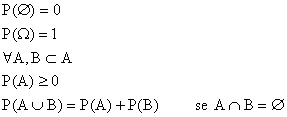
Notiamo che la definizione di Laplace  verifica le proprietà assiomatiche precedenti.

Tramite i teoremi sulle probabilità possiamo poi calcolare la probabilità di tutti gli eventi complessi contenuti in A

Teorema della probabilità totale

Se A e B sono due insiemi non disgiunti di  W

Possiamo esprimere l'insieme come unione di due insiemi disgiunti, di cui sappiamo calcolare la probabilità sulla base delle proprietà assiomatiche

A  sua volta, l'insieme A puo' essere scritto come l'unione di due insemi disgiunti:

per cui:

ne segue che

e quindi

Nel caso del lancio del dado, supponiamo che A sia l'insieme dei risultati pari e B sia l'insieme dei primi due risultati pari e del 5, l'insieme unione sarà:

L'intersezione sarà

P ( )=P( )=4/6=P( )+P( )-P(

La probabilita' condizionata e l'indipendenza stocastica di due eventi

Definiamo la probabilità di un evento A condizionata ad un evento B.

Con lo stesso ragionamento fatto per le distribuzioni condizionate nelle variabili statistiche a due dimensioni si ha che

Il fatto che l'evento B si sia verificato, fa si' che la probabilita' di B sia pari a 1, ovvero costitusce il nuovo insieme deglieventi possibili (che era W). P(A|B) e' allora la probabilita' dell'evento A pensato come sott'insieme di B. Tale probabilita' si ottiene dividendo la probabilita' di quella parte di A che sta in B, P(A B), riferita all'insieme W per la probabilita' di B sempre riferita a W. Se A coincide con B, ritroviamo cosi' che P(B|B)=1.

Due eventi si dicono indipendenti stocasticamente se

=P(A)

Ovvero se il fatto di sapere che si è verificato l'evento B, P(B)=1, cioe' che l'insieme dei risultati dell'esperimento è ridotto a B, non cambia la probabilità di A.

Teorema della probabilità composta

Ciò premesso, il teorema della probabilità composta afferma che condizione necessaria e sufficiente affinchè due eventi siano stocasticamente indipendenti è che la probabilita dell'intersezione si spacchi nel prodotto delle probabilità dei singoli eventi.

Condizione necessaria

Se    (ipotesi)

Allora   A e B sono stocasticamente indipendenti, cioè (tesi).

Infatti che in base all'ipotesi diventa

Condizione sufficiente

Se (ipotesi)

Allora   (tesi)

Infatti , e in base all'ipotesi  , ne segue che

=P(A)  e quindi che

Teorema di Bayes

Supponiamo di suddividere lo spazio dei risultati W possibili di un esperimento in n sott'insiemi disgiunti B_i i=1,2,.,n.

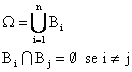
Sia inoltre A un sott'insieme di W. Il teorema di bayes permette di calcolare la probabilita' di ciascuna partizione B_i condizionata all'evento A, ovvero quando l'insieme dei risultati e' ristretto al sott'insieme A di W, quando siano note le probabilita' di A condizionate a ciscuno dei sott'insiemi B_i.

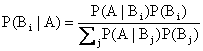
Infatti

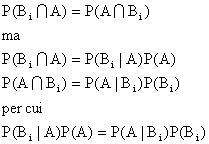
ovvero

(*)

L'insieme A d'altra parte puo' essere pensato come

ovvero come unione di insiemi disgiunti tra loro.

Per il teorema della probabilita' totale allora

che sostituita nella (*) ci da' la formula di Bayes.