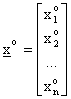
Il campione bernoulliano di n componenti, frutto di n estrazioni dalla stessa variabile mono-dimensionale, puo' essere pensato come il risultato di una unica estrazione da una variabile casuale n-dimensionale. Tale variabile e' detta variabile campionaria.

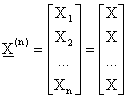
Le distribuzioni marginali delle n componenti di tale variabile sono tutte uguali alla distribuzione di X. Essendo le componenti stocasticamente indipendenti tra loro, la distribuzione congiunta sara' il prodotto delle distribuzioni marginali .

Segue che la media di tale variabile, vettore a n componenti ognuna ottenuta facendo la media della componente corrispondente della variabile campionaria, avra' componenti tutte uguali fra loro e pari a

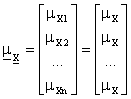
La matrice di varianza-covarianza della variabile campionaria, essendo tutte le componenti indipendenti tra loro, avra' coefficienti di covarianza tutti nulli e essendo le singole componenti tutte pari a X le varianze di ciascuna di esse saranno tutte uguali fra loro e pari a

Stimatori e stime

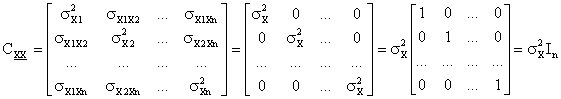
Calcoliamo media m e varianza s² del campione come nel caso di una variabile statistica. Ci chiediamo in che relazione siano tali valori campionari con la media e la varianza che vogliamo stimare.

Per far cio' occorre pensare alle espressioni della media e della varianza come dei legami tra la variabile casuale campionaria e rispettivamente la variabile casuale mono-dimensionale media campionaria e quella sempre mono-dimensionale della varianza campionaria.

Le variabili casuali funzioni della variabile campionaria si dicono stimatori. M e' lo stimatore media campionaria e S² lo stimatore varianza campionaria. Il valore assunto da tali stimatori in corrispondenza di un vettore di osservazioni estratto dalla variabile campionaria si dice stima, rispettivamente della media e della varianza. La stima puo' pensarsi come una estrazione dalla variabile stimatore.

Le proprieta' della stime ottenute a partire da un certo stimatore si definiscono sulla base della distribuzione dello stimatore.

Vediamo due di queste proprieta': la correttezza e la consistenza.

Correttezza

Uno stimatore si dice corretto se la media della sua distribuzione coincide con il parametro che tramite esso si vuole stimare.

La media campionaria e' uno stimatore corretto della media di X.

La varianza campionaria non e' uno stimatore corretto. Si puo' dimostrare che:

Pertanto uno stimatore corretto della varianza campionaria sara':

detto varianza campionaria corretta.

In tal caso infatti:

Uno stimatore corretto della varianza campionaria si ottiene dividendo la somma dei quadrati degli scarti del campione per la numerosita' n diminuita di 1.

Consistenza

Uno stimatore si dice consistente se al tendere della numerosita' del campione ad infinito la sua distribuzione si concentra intorno alla media ovvero la probabilita' che esso assuma il valore della media tenda a 1. Condizione sufficiente per la consistenza di uno stimatore e' che al tendere di n a infinito la sua media tenda al parametro che con esso si vuole stimare e la sua varianza tenda a zero.

Sia la media che la varianza campionaria corretta sono stimatori consistenti.

Il principio dei minimi quadrati

Introduzione

Nell'ambito del problema della stima dei parametri da cui dipende la distribuzione della variabile casuale che descrive i risultati di un esperimento stocastico a partire da un campione bernoulliano, affrontiamo la questione della definizione di un principio in base al quale determinare gli stimatori, ovvero le stime dei parametri cercati.

Vedremo soltanto un criterio che va sotto il nome di principio di minimi quadrati, che in realta', come approfondiremo in seguito, ha un campo di applicazione ben piu' ampio di quello che abbiamo delineato.

Vediamo dunque come si applica tale criterio nel caso della stima della media e della varianza di una variabile casuale da cui si estrae un campione bernoulliano.

Il risultato dell'esperimento descritto dalla variabile nell'ambito dei minimi quadrati e' la quantita' osservata che indicheremo con y^o.

Il problema si traduce nel seguente modo:

si dispone di un numero n di osservazioni di una stessa grandezza, che si pensano estratte da una variabile casuale campionaria a n dimensioni. Le componenti della media di tale variabile soddisfano a n relazioni lineari parametriche, che costituiscono il modello funzionale dei minimi quadrati: nel nostro caso le componenti  sono tutte uguali fra loro e dunque vengono poste tutte uguali a un unico parametro incognito x, pari alla media della variabile da cui abbiamo estratto il campione. Si conosce inoltre a meno di un coefficiente di proporzionalita' la matrice di varianza covarianza della variabile campionaria.

Nel caso di n osservazioni indipendenti e di egual precisione di una stessa grandezza essa sara' proporzionale all'identita'.

La matrice di covarianza della variabile campionaria si dice modello stocastico dei minimi quadrati e dipende dalla modalita' con cui si sono fatte le osservazioni.

Rappresentiamo ora le componenti del campione in funzione di una variabile etichetta (ad esempio il tempo in cui e' avvenuta l'osservazione).

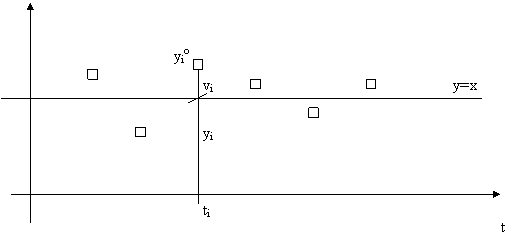
t

Il parametro incognito, e quindi la media della variabile campionaria, viene ricercato come quello che rende minima la somma dei quadrati degli errori d'osservazione, detta funzione obiettivo.

La somma di quadrati degli scarti e' proporzionale alla varianza del campione, quello che cerchiamo dunque e' il valore della media del campione che minimizza tale varianza.

Il valore di x, stima che indichiamo con , per cui essa e' minima e' quello per cui la sua derivata rispetto a x si annulla ed e' dato da:

La stima del parametro x coincide con la media campionaria. Da essa possiamo ricavare la stima della media della variabile campionaria, che non e' altro che il vettore n-dimensionale con componenti tutte uguali fra loro e paria al parametro stimato.

La varianza della grandezza osservata, in questo caso, e' rappresentata dal termine di proporzionalita' incognito del modello stocastico dei minimi quadrati.

Una stima di tale termine viene ottenuta utilizzando la seguente espressione:

Si osservi che il legame trovato tra il campione osservato e il parametro incognito puo' pensarsi come legame tra la variabile casuale campionaria Y  a n dimensioni e la variabile casuale X a 1 dimensione stimatore del parametro x.

Tale stimatore e' corretto e consistente e la sua varianza  ricavata per propagazione dalla covarianza della variabile campionaria e' data da:

Esprimiamo ora il problema in termini matriciali che si prestano alla generalizzazione. Si avra':

il campione osservato

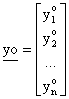
la variabile campionaria da cui e' estratto il campione

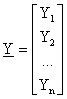
la media della variabile campionaria

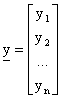
il modello funzionale parametrico

, ovvero in forma matriciale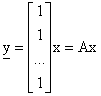

il modello stocastico

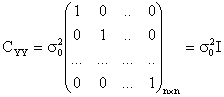
la funzione obbiettivo

Il principio di minimi quadrati

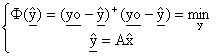
La stima dei parametri da cui dipende la media

La stima della media della variabile campionaria

La stima del fattore diproporzionalita' della matrice di convarianza della variabile campionaria

Lo stimatore dei parametri

Lo stimatore del vettore media

Lo stimatore del termine di proporzionalita' della matrice di covarianza della variabile campionaria

Inoltre si hanno per propagazione della covarianza (nel caso lineare)

La varianza dello stimatore dei parametri

La varianza-covarianza dello stimatore del vettore media

Osserviamo che nessuna ipotesi e' stata fatta sulla distribuzione della variabile da cui e' estratto il campione. Il principio puo' essere applicato anche nel caso in cui le osservazioni siano relativa a variabili con medie diverse tra loro, e le osservazioni non siano di egual precisione e indipendenti tra loro. Il campione di osservazioni non deve cioe' essere necessariamente bernoulliano.

Generalizziamo per gradi  il principio dei minimi quadrati, applicandolo dapprima alla stima della media di un campione di osservazioni relative a una stessa grandezza ma effettuate con precisioni diverse e quindi al caso di osservazioni indipendenti e di egual varianza, ma con media dipendente linearmente dal tempo.

Caso #2: La media ponderata

Supponiamo che rispetto al caso precedente le misure vengano fatte con precisione diversa., ma sempre in maniera indipendente.

La matrice di covarianza della variabile campionaria sara' in questo caso ancora diagonale ma le varianza delle singole componenti saranno diverse tra loro.

Il problema e' sempre quello della stima della retta orizzontale che interpola meglio i dati.

Si puo' ragionevolmente supporre che in tal caso osservazioni con precisione minore (ovvero con varianza maggiore) si discostino di piu' dal valore teorico. Per fare in modo che la retta stimata rimanga piu' distante da tali osservazioni e si avvicini di piu' a quelle piu' precise, bastera' minimizzare la somma dei quadrati degli scarti ciascuno diviso per la radice della varianza relativa.

La funzione obbiettivo diverra' allora pari a:

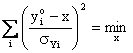
e dunque il parametro incognito:

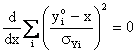
La varianza della grandezza osservata, in questo caso, e' rappresentata dal termine di proporzionalita' incognito del modello stocastico dei minimi quadrati.

Una stima di tale termine viene ottenuta utilizzando la seguente espressione:

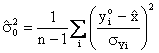
Caso #3: La regressione lineare semplice

Un ulteriore generalizzazione dei minimi quadrati e' quello della stima della media di una variabile campionaria, quando questa non sia costante ma vari linearmente nel tempo. Supponiamo in tal caso che le osservazioni siano sempre indipendenti e di egual varianza.

In questo caso le osservazioni non oscilleranno a causa degli errori di misura intorno a una retta orizzontale, bensi' intorno a una retta inclinata la cui equazione dipendera' da due parametri a e b incogniti. Anche in questo la stima di tali parametri viene fatta cercando il minimo della somma dei quadrati degli scarti tra ciascuna osservazione e la media espressa in funzione dei due parametri.

Il modello funzionale diviene:

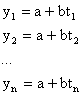, ovvero in forma matriciale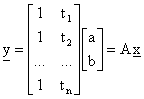

con A matrice rettangolare con numero di righe pari al numero di osservazioni e numero di colonne pari al numero dei parametri, ovvero 2

il modello stocastico, matrice quadrata di ordine n

la funzione obbiettivo

Il principio di minimi quadrati

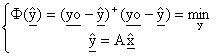
La stima dei parametri da cui dipende la media, vettore a 2 dimensioni

La stima della media della variabile campionaria, a n dimensioni

La stima del fattore diproporzionalita' della matrice di convarianza della variabile campionaria

Lo stimatore dei parametri, variabile casual e a 2 dimensioni

Lo stimatore del vettore media, variabile casuale a n dimensioni

Lo stimatore del termine di proporzionalita' della matrice di covarianza della variabile campionaria

Inoltre si hanno per propagazione della covarianza (nel caso lineare)

La matrice di varianza covarianza dello stimatore dei parametri, matrice quadrata di ordine 2

La varianza-covarianza dello stimatore del vettore media, matrice quadrata di ordine n

Osservazione:

Il principio dei minimi quadrati puo' applicarsi anche nel caso in cui il campione e' ottenuto dalla misura di n grandezze diverse tra loro, descritte ognuna cioe' da una diversa variabile casuale, ottenute anche non in maniera indipendente e non con la stessa precisione. Il campione sara' pensato come una estrazione da una variabile casuale  a n dimensioni, in cui le medie delle singole componenti sono diverse tra loro e la matrice di covarianza e' una matrice piena in cui le varianze sono in generale diverse.

Le formule in questo caso diventano:

Con A matrice di dimensioni n×m

il modello stocastico

con Q matrice quadrata, simmetrica, piena e di dimensione n×n

la funzione obbiettivo

Il principio di minimi quadrati

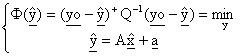
La stima dei parametri da cui dipende la media, vettore di m componenti

La stima della media della variabile campionaria, vettore di n componenti

La stima del fattore di proporzionalita' della matrice di convarianza della variabile campionaria

Lo stimatore dei parametri, variabile casuale m-dimensionale

Lo stimatore del vettore media, variabile casuale n-dimensionale

Lo stimatore del termine di proporzionalita' della matrice di covarianza della variabile campionaria, variabile casuale mono-dimensionale

Inoltre si hanno per propagazione della covarianza (nel caso lineare)

La varianza dello stimatore dei parametri, matrice quadrata di ordine m

La varianza-covarianza dello stimatore del vettore media, matrice quadrata di ordine n