Associamo ad  W i punti 1,2,3,4,5,6 della retta reale (si potrebbe ovviamente scegliere una corrispondenza diversa, cioè una variabile casuale diversa), ovvero rappresentiamo l'insieme dei risultati tramite una variabile casuale a una dimensione (i cui valori sono cioè punti dell'asse reale), discreta e finita.

Per rappresentare  la probabilità dei risultati riportati sull'asse reale per ogni variabile casuale X si definisce la funzione di distribuzione F_X(x).

Fissato un valore x sull'asse reale è definito il sott'insieme , la funzione di distribuzione assume in a il valore della probabilita' di tale sott'insieme

F(x)=P(A_x)

F(x), e' definita su tutto l'asse reale, e' compresa tra 0 e 1 ed e' sempre crescente.

Nel caso in esame di variabile discreta e finita la funzione di distribuzione e' costante a tratti: in corrispondenza dei valori argomentali essa si incrementa della probabilità corrispondente.

Inoltre è facile vedere che:

Infatti, se consideriamo gli eventi A,B,C così definiti:

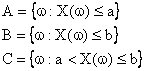
si ha che

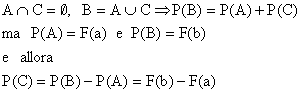
Nel caso semplice del lancio di un dado non truccato, in cui ad ogni elemento di W e' associata probabilita' pari a 1/6, la funzione di distribuzione è data da

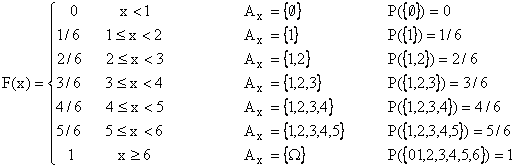
Se ora proviamo a effettuare N lanci del dado e ordiniamo i risultati in una variabile statistica, rappresentandone i valori argomentali sull'asse reale, la variabile casuale e la variabile discreta saranno formalmente identiche: ad ogni valore argomentale si associerà nel caso del modello una probabilità e nel caso della statistica una frequenza relativa che godono delle stesse proprietà, si associerà al modello una funzione di distribuzione e alla statistica una funzione cumulativa di frequenza di nuovo con le stesse proprietà.

La variabile casuale con le probabilità associate rappresenta cosa ci si aspetta come risultato dell'esperimento, la statistica cosa si è ottenuto eseguendo l'esperimento. Le frequenze ottenute saranno diverse ogni qualvolta si ripeterà l'eserimento N volte, il modello sarà sempre uguale. La funzione del modello è quella di prevedere quale  frequenza possiamo attenderci dalla effettiva ripetizione dell'esperimento aleatorio.

Si osservi come anche l'indagine volta a rilevare la distribuzione di una certa caratteristica in una popolazione possa essere assimilata alla ripetizione di un esperimento stocastico che abbia come risultati possibili la caratteristica in esame.

Di una variabile discreta e finita mono dimensionale si calcolano media e varianza in modo formalmente identico a quello utilizzato per le variabili statistiche monodimensionali a patto di sostituire le frequenze con le probabilità.

Si può definire analogamente l'operatore media, introdurre variabili casuali funzioni di altre e enunciare il teorema della media.

Esempi di variabili casuali discrete mono-dimensionali

La distribuzione binomiale

La distribuzione binomiale indica la probabilità con cui su n ripetizioni indipendenti di un esperimento con due soli possibili risultati (successo e insuccesso, 0 e 1) k siano dei successi.

Fissato il numero di ripetizioni n e la probabilità che si verifichi il successo nella singola ripetizione p, per ogni valore di k, la probabilità è fornita dalla seguente legge

Media e varianza della distribuzione binomiale sono date da

m=np(1-p)

s =np

La distribuzione poissoniana

Supponiamo che il numero di ripetizioni di ripetizioni indipendenti di un esperimento con due soli possibili risultati (successo e insuccesso) diventi molto grande e che in corrispondenza la probabilità del successo diventi molto piccola in modo che il loro prodotto si mantenga costante np=l. In tal caso la distribuzione del numero di successi è data dalla seguente espressione ed è detta di Poisson:

Media e varianza della distribuzione binomiale sono date da

m l

s l

La distribuzione di Poisson serve a prevedere la frequenza del numero di eventi rari (p del successo è molto piccola) su un numero elevato di prove.

Variabile casuale discreta a 2 dimensioni

Nel caso in cui l'esperimento casuale presenti coppie di risultati, come ad esempio nel caso del lancio contemporaneo di due monete, l'insieme Ω sarà naturalmente messo in corrispondenza con i punti del piano cartesiano R². Ad esempio nel caso del lancio di due monete non truccate Ω, posto testa =0 e croce =1, sarà rappresentabile tramite la variabile casuale 2d che assume i valori (0,0),(0,1),(1,0),(1,1).

Per rappresentare  la probabilità dei risultati riportati sul piano reale, per ogni variabile casuale (X,Y) si definisce la funzione di distribuzione F_XY(x,y).

Fissata una coppia di valori (x,y) sul piano è definito il sottoinsieme . La funzione di distribuzione assume in (a,b) il valore della probabilita' di tale sott'insieme

F_XY(x,y)=P(Axy)

F_XY(x,y), e' definita su tutto R², e' compresa tra 0 e 1 ed e' sempre crescente.

Nel caso in esame di variabile doppia discreta e finita la funzione di distribuzione e' discontinua: in corrispondenza dei valori argomentali essa si incrementa della probabilità corrispondente.

Anche in questo caso

Come già nel caso monodimensionale il modello e la statistica bidimensionali sono formalmente analoghe, l'una raccoglie i risultati possibili, l'altra quelli registrati ripetendo l'esperimento. A tali risultati (coppie di valori) nell'un caso si associano probabilità congiunte, nell'altro frequenze congiunte con le stesse proprietà formali. Alla variabile casuale si associa una funzione di distribuzione alla statistica una funzione cumulativa di frequenza.

Si definiscono inoltre le probabilità marginali, le probabilità condizionate, il vettore media e la matrice di covarianza, ottenute sostituendo alla frequenza la probabilità . Si definisce infine l'operatore media e introdotte le trasformazioni tra variabili casuali si enuncia analogamente il teorema della media.

Distribuzioni condizionate, indipendenza stocastica tra le componenti di una variabile doppia.

La distribuzione condizionata di una delle componenti della variabile doppia ad un valore dell'altra componente è data per la X da

per la Y da

Il significato è lo stesso già visto per le variabili statistiche.

La componente X (oY) è stocasticamente indipendente dalla componente Y (o X), se le distribuzioni condizionate ai valori della Y (o X) sono tutte uguali tra loro e pari alla marginale.

Condizione necessaria e sufficiente affinchè le componenti della variabile doppia siano stocasticamente indipendenti è che la distribuzione di probabilità congiunta si spacchi nel prodotto delle marginali:

Condizione sufficiente

Ip.

Th.:

Infatti

Condizione necessaria

Ip.:

Th.:

Infatti

Conseguenza dell'indipendenza stocastica

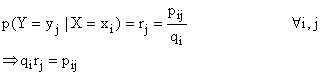
Se le componenti di una variabile doppia sono stocasticamente indipendenti tra loro, il coefficiente di coverianza è pari a 0 e la matrice di covarianza è diagonale.

Infatti   

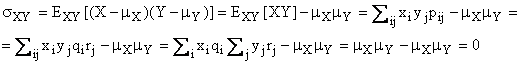
Si osservi che il fattto che il coefficiente di correlazione sia uguale a zero non è una condizione sufficiente per concludere che le componenti sono stocasticamente indipendenti.

L'indice di correlazione lineare

Se le componenti di una variabile doppia sono stocasticamente indipendenti allora

D' altra parte se tra le componenti esiste un legame lineare Y=aX+b

e essendo

il rapporto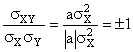

Questo rapporto si chiama indice di correlazione lineare, si dimostra che varia infatti tra 0 e ±1 al variare della relazione tra le componenti della variabile doppia dalla indipendenza al legame lineare.

Si osservi che se le componenti sono indipendenti sono incorrelate (covarianza paria zero) e linearmente indipendenti.

Se sono linearmente indipendenti (indice di correlazione pari a zero) sono anche incorrelate ma non necessariamente stocasticamente indipendenti.