MODULAZIONE SU PORTANTE SINUSOIDALE

tecnica

MODULAZIONE SU PORTANTE SINUSOIDALE

La forma del generico segnale modulato è:

frequ 313e44d enza portante

deviazione istantanea di frequ 313e44d enza

frequ 313e44d enza istantanea

inviluppo

fase istantanea

deviazione istantanea di fase

    f₀

La modulazione consiste in una:

mod. di fase

Alterazione di A(t)    modulazione di ampiezza

mod. di requenza

Alterazione di j(t)    modulazione angolare 

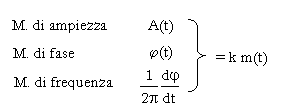Le alterazioni sono influenzate da un segnale modulante m(t); in particolare:

In tutti e tre i casi c'è una traslazione dello spettro di m(t) (nel caso di modulazione angolare c'è anche una variazione dell'ampiezza della banda). Ciò può essere visto mediante i seguenti passaggi:

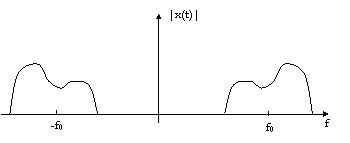
Questo equivale in frequ 313e44d enza a traslare verso destra lo spettro di di un fattore f₀ e altrettanto verso sinistra lo spettro di , che essendo il coniugato del precedente, avrà lo stesso spettro ma coniugato e cambiato di segno (vedi proprietà della trasformata di Fourier); quindi il suo modulo sarà il simmetrico dell'altro e la fase la antisimmetrica, come è giusto che sia, dato che x(t) è reale. Se la banda occupata da è minore di f₀ (in genere è molto minore), allora i due spettri saranno nettamente staccati e uno si troverà tutto a frequ 313e44d enze positive e l'altro a frequ 313e44d enze negative (vedi figura).

Il segnale x(t) è detto inviluppo complesso.

Se filtriamo X(f) con un filtro u_-1(f) otteniamo solo la parte di spettro a frequ 313e44d enze positive:

    segnale analitico

Osserviamo che x(t) = Re[2x⁺(t)].

Poiché la trasformata di u_-1(t) è allora:

è il filtro di Hilbert, ed ha H(f)=-jsign(f)

altro modo di scomporre x(t)

xc(t)

xs(t)

Osserviamo che:

,   

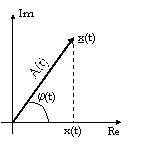
Infine, l'inviluppo complesso è interpretabile come un vettore nel piano complesso il cui modulo si allunga e si accorcia nel tempo e che ruota a causa della variabilità della fase. Il segnale analitico è l'inviluppo complesso a cui si aggiunge un moto rotatorio a frequ 313e44d enza f₀. La componente sull'asse reale di questo vettore è proprio x(t).