|
|
| |
Teoria in sintesi
PARABOLA
Ogni funzione ![]() ,
con a 0, rappresenta una parabola, con le seguenti caratteristiche:
,
con a 0, rappresenta una parabola, con le seguenti caratteristiche:
L'asse della parabola è parallelo all'asse delle y
Il vertice ha ascissa ![]() (l'ordinata si può t 616c23g rovare sostituendo questo
valore nella funzione)
(l'ordinata si può t 616c23g rovare sostituendo questo
valore nella funzione)
La parabola ha la concavità rivolta verso l'alto se ![]() ,
verso il basso se
,
verso il basso se ![]()
La "apertura" della parabola è tanto maggiore, quanto
maggiore è ![]() .
.
Per tracciare il grafico qualitativo della parabola si determinano il
vertice ![]() e le intersezioni con gli assi.
e le intersezioni con gli assi.
N.B.: Per queste ultime ricorda che devi risolvere i due sistemi
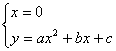 che dà
che dà ![]()
![]()
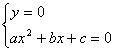 che dà
che dà ![]()
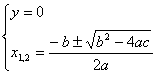
DISEQUAZIONI DI 2º GRADO
![]()
N.B.: Possiamo sempre fare riferimento ai casi in cui il coefficiente a è positivo. Infatti se a è negativo, basta cambiare segno a tutti i termini e invertire il senso delle disequazioni.
(esempio: ![]() è equivalente a
è equivalente a 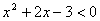
METODO GRAFICO (uso della parabola)
Per dare una interpretazione grafica delle disequazioni di secondo grado
![]()
a) a) si disegna la parabola;
b) b) si cercano gli eventuali punti di intersezione della parabola con l'asse x;
c) c) si considerano le soluzioni delle disequazioni che sono
date dalle ascisse dei punti della parabola che hanno ordinata positiva ![]() oppure negativa
oppure negativa ![]() .
.
I casi possibili risultano riassunti nel seguente schema:
![]()
|
|
|
|
![]()
Costruisci tu per questo caso lo schema riassuntivo in modo analogo. Ricorda che in questo caso si procede considerando la parte di parabola che sta nel semipiano delle y negative.
DECOMPOSIZIONE DEL TRINOMIO DI SECONDO GRADO
La risoluzione analitica delle disequazioni
![]()
avviene nel modo seguente
![]() dette
dette ![]() le due soluzioni di
le due soluzioni di ![]() e posto
e posto ![]() si ha
si ha
![]()
E quindi, dalle regole dei segni, otteniamo la soluzione
![]()
(N.B.: Il simbolo ![]() ,
preso in prestito dalla logica, sta a significare che si considera l'unione dei
due insiemi
,
preso in prestito dalla logica, sta a significare che si considera l'unione dei
due insiemi ![]() ).
).
quindi soluzione
![]()
soluzione
Invece
per la disequazione ![]() in modo analogo si ottiene:
in modo analogo si ottiene:
Svolgere per esercizio uno schema analogo al caso precedente.
RISOLUZIONE GRAFICA DI UNA DISEQUAZIONE DI II GRADO
Ricordando che:
i.tutti i punti della parabola di equazione y=ax2+bx+c hanno coordinate della forma (x;ax2+bx+c): le loro ordinate, infatti, si ottengono sostituendo alla variabile x i valori numerici scelti per le ascisse;
ii.quando si risolve una disequazione di II grado quale ax2+bx+c>0 si cercano quei valori reali che, sostituiti alla variabile x nell'espressione a primo membro, danno un risultato positivo;
si deduce che per risolvere una disequazione di II grado del tipo ax2+bx+c>0 (o ax2+bx+c<0) è possibile procedere graficamente nel modo seguente:
disegnando la parabola grafico dell'equazione y=ax2+bx+c,
individuando tutti quei valori di ascissa dei punti della parabola che hanno ordinata positiva (o negativa).
Le situazioni che si possono presentare sono le seguenti:
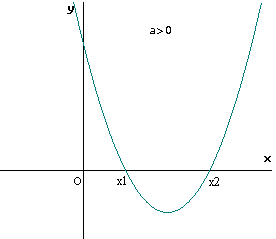
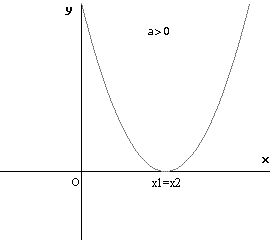
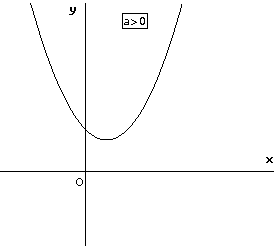
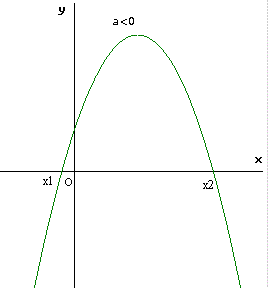
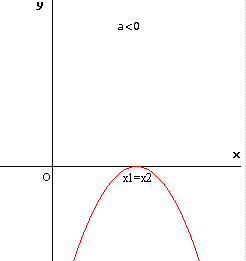
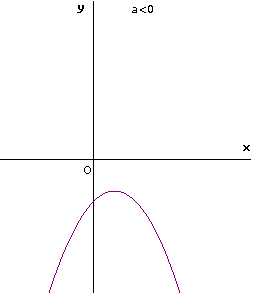
dove con x1 e x2 sono stati indicati i valori delle ascisse dei punti (eventualmente coincidenti) in cui la parabola interseca l'asse x, detti anche ZERI della funzione quadratica.
I diversi casi dipendono dai seguenti elementi:
il segno del coefficiente a, che determina se la parabola associata alla disequazione rivolge la concavità verso l'alto (a>0) o verso il basso (a<0);
il segno del discriminante Δ che determina se il trinomio ha due zeri reali e distinti (Δ>0), due zeri reali coincidenti (Δ =0) oppure nessuno zero reale (Δ<0);
il simbolo di disuguaglianza > o < che determina quali punti della parabola si devono prendere in considerazione per individuare le soluzioni: quelli con ordinata positiva se compare il simbolo >, quelli con ordinata negativa se compare il simbolo <.
Considerando il caso a>0, sono qui di seguito rappresentate tutte le situazioni possibili:
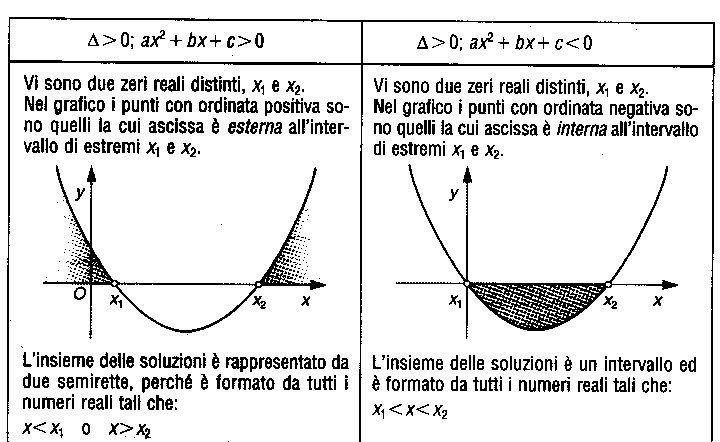
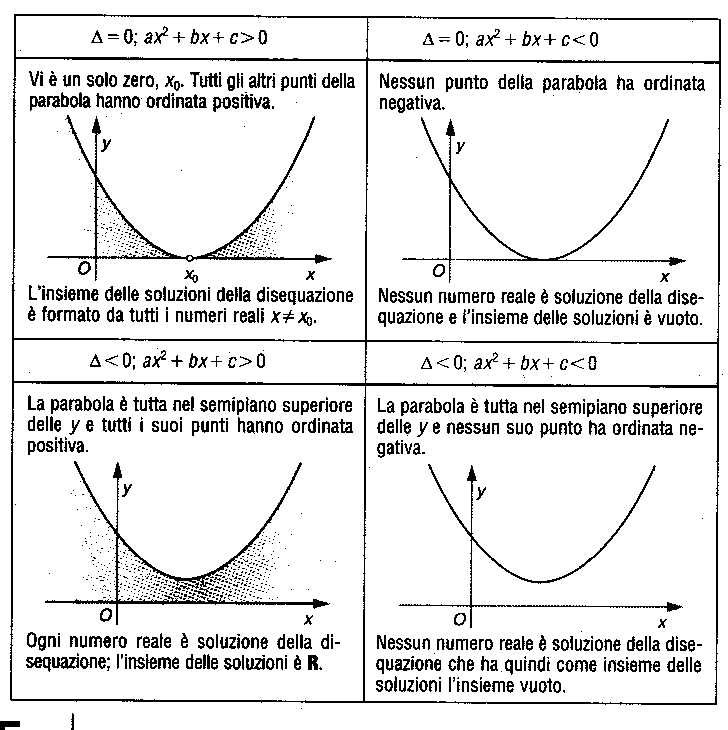
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025