Relazione sui metodi d'integrazione numerica

matematica

Relazione sui metodi d'integrazione numerica

Il calcolo di un integrale definito può essere laborioso fornendoci un valore con una precisione per noi inutile. Per semplificarne il calcolo avendo in ogni caso dei valori che non si discostino molto da quello reale, è necessario utilizza 323f52d re i metodi d'integrazione numerica.

In generale ognuno di questi metodi consiste nello scomporre l'intervallo di integrazione [a , b] in più intervalli di ampiezza , dove è il numero di sottointervalli in cui si vuole suddividere [a , b]. Una volta ottenuti questi intervalli, è possibile costruire su di essi una serie di figure geometriche, le cui somma delle aree riesca ad approssimare più o meno fedelmente il volume dell'integrale definito che noi calcoliamo grazie al Teorema di Torricelli.

Esistono tre metodi di approssimazione, che differiscono in base a quale figura geometrica viene costruita su ogni intervallo (cioè ):

dei RETTANGOLI, dei TRAPEZI e di SIMPSON.

Il metodo dei rettangoli costruisce su ogni un rettangolo di base e altezza il minimo (approssimazione per difetto) o il massimo (approssimazione per eccesso) della funzione in quell'intervallo, è il meno preciso dei tre metodi ma è di semplice realizzazione, infatti la sua formula è

: plurirettangolo inscritto

: plurirettangolo circoscritto.

Il metodo dei trapezi è molto più preciso rispetto a quello dei rettangoli, infatti costruisce su ogni un trapezio rettangolo la cui base maggiore è il massimo della funzione nell'intervallo , la base minore ne è il minimo mentre l'altezza è .

La formula per approssimare il valore di un integrale con questo metodo è

.

Infine il metodo più preciso è quello di Cavalieri - Simpson che approssima un integrale definito per mezzo di parabole. La sua formula è:

.

Questa formula scaturisce dall'applicazione per ogni intervallo della formula , che si ricava considerando un trapezoide formato da due rette parallele all'asse distanti tra loro di una distanza , cioè di ordinata e -, dall'asse e da una parabola di equazione , applicando alla i valori , - e 0 abbiamo tre equazioni:

(1)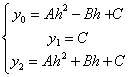 dalle quali ricaviamo i valori dei coefficienti A, B e C che utilizziamo nell' integrale 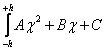che sarà uguale a 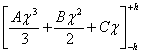cioè , che non è altri che , infatti considerando , e dal sistema (1) abbiamo la formula che applicata ad ogni intervallo della funzione consente di avere la formula del metodo di Simpson enunciata prima.

ESEMPIO D' INTEGRAZIONE NUMERICA:

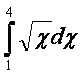  n=4

Metodo dei RETTANGOLI

=4.278

Metodo dei TRAPEZI

=4.653

Metodo di Cavalieri - Simpson