|
|
| |
PROGRAMMAZIONE LINEARE
La quantità da ottimizzare si chiama FUNZIONE OBIETTIVO
La quantità a disposizione, il cui valore è da scegliere per realizzare l'ottimizzazione, si dice VARIABILE D'AZIONE.
Per risolvere i sistemi di disequazioni lineari in 2 incognite, si individuano i semipiani che soddisfano ciascuna delle disequazioni del sistema. La parte di piano comune ai semipiani individuati rappresenta la soluzione del sistema. Questa regione può essere limitata o illimitata.
Le relazioni che legano le variabili e i vincoli a cui sono soggette conducono a un sistema di disequazioni di 1° grado, risolvendo il quale si ottengono le soluzioni. La soluzione è data dall'intersezione dei semipiani individuati dal sistema. La soluzione ottimale è uno dei vertici.
TEORIA DELLE RETTE
Formula del fascio di rette passanti per un punto dato:
Y-Yp = m(X-Xp)
LE CONICHE
Le coniche sono delle linee che si ottengono
dall'intersezione nello spazio tra una superficie conica e un piano. Le coniche
principali sono
La circonferenza (cfr) è l'insieme dei punti del piano equidistanti da un punto fisso detto CENTRO. La distanza si chiama RAGGIO.
P(x,y)


C (ά, β)
PC = r
(x-ά)2 + (y-β)2 = r2 EQUAZIONE ESPLICITA PER TROVARE IL RAGGIO
I punti del piano che appartengono alla cfr. di centro C e raggio r sono quelli che soddisfano l'equazione PC = r
ESEMPIO:
C (1, 3) e raggio r = 4
(x-1)2 + (y-3)2 = 16
Sviluppando l'espressione esplicita appena trovata si ottiene la 2^ equazione della cfr.
x2 + y2 + ax + by + c = 0 EQUAZIONE IMPLICITA
FORMULE DI PASSAGGIO
a
= -2ά b
= -2β c
= ά2 + β2 - r2
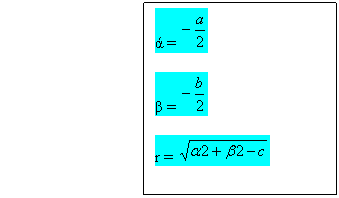
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025