|
|
| |
= MATEMATICA APPLICATA ALL'ECONOMIA =
Funzione di domanda
x → quantità di merce richiesta (variabile dipendente)
p → prezzo della merce (variabile indipendente)
Principali funzioni di domanda
![]()
![]()
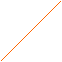
![]() Funzione lineare: x = a - b ∙ p con a
> 0 e b > 0
Funzione lineare: x = a - b ∙ p con a
> 0 e b > 0
segmento di retta decrescente
![]()
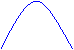
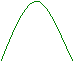
![]() Funzione di secondo grado: x = a - b ∙
p2 con a > 0 e b > 0
Funzione di secondo grado: x = a - b ∙
p2 con a > 0 e b > 0
arco di parabola decrescente
|
x = |
a |
- b |
|
p + c |
![]()
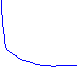
![]() Funzione
fratta: con a >
0, b > 0 e c > 0
Funzione
fratta: con a >
0, b > 0 e c > 0
asse di iperbole equilatera
Elasticità della domanda
L'elasticità della domanda indica la sensibilità della domanda rispetto alle variazioni del prezzo.
p1; p2 → due prezzi dello stesso bene p1 < p2
x1 → quantità domandata in corrispondenza di p1
x2 → quantità domandata in corrispondenza di p2
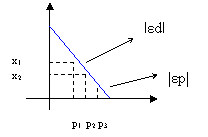
|
Δp |
|
p2 - p1 |
→ variazione relativa del prezzo |
|
p1 |
p1 |
|
x |
|
x2 - x1 |
→ variazione relativa della domanda |
|
x1 |
x1 |
|
|εd| = |
x |
|
x |
|
p1 |
|
x |
|
p1 |
|
x2 - x1 |
|
p1 |
→ elasticità dell'arco |
|
x1 |
||||||||||||||
|
p |
x1 |
p |
p |
x1 |
p2 - p1 |
x1 |
||||||||
|
p1 |
d| < 1 → domanda rigida
|εd| > 1 → domanda elastica
|εd| =1 → domanda anelastica (fissa, invariabile)
Se, invece, voglio conoscere l'elasticità in un punto uso l'elasticità puntuale.
|
|εp| = |
f1(p) ∙ |
p |
→ elasticità puntuale |
|
f(p) |
Funzione di offerta
x → quantità offerta di un dato bene (x ≥ 0) (variabile dipendente)
p → prezzo del bene (variabile indipendente)
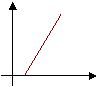
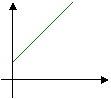
Funzione lineare: x = a ∙ p - b
|
|εo| = |
Δx |
|
p1 |
|
x2 - x1 |
|
p1 |
→ elasticità dell'offerta |
|
Δp |
x1 |
p2 - p1 |
x1 |
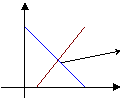
Equilibrio di domanda e offerta
x = f(p) → funzione di domanda x = g(p) → funzione di offerta
f(p) = g(p) → equilibrio
E (p*; q*)
![]()
![]()
![]() Costi fissi: non dipendono dalla
quantità prodotta (affitti, stipendi dipendenti.)
Costi fissi: non dipendono dalla
quantità prodotta (affitti, stipendi dipendenti.)
![]()
![]() Costi variabili: dipendono dalla quantità
prodotta (materie prime, consumo energetico, manutenzione impianti.)
Costi variabili: dipendono dalla quantità
prodotta (materie prime, consumo energetico, manutenzione impianti.)
Costi totali: sono la somma dei costi fissi e variabili
Principali funzioni di costo totale
Funzione lineare: G(x) = ax + b con x ≥ 0 e a;b > 0
![]()
![]()
![]()
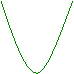
![]() Funzione quadratica: G(x) = ax2 + bx
+ c con x ≥ 0
Funzione quadratica: G(x) = ax2 + bx
+ c con x ≥ 0
a > 0 e b;c ≥ 0 a
< 0 e b;c ≥ 0
![]()
![]()
![]() Funzione esponenziale: G(x) = aebx
con a;b > 0
Funzione esponenziale: G(x) = aebx
con a;b > 0
Costo unitario
|
Cu(x) = |
CT(x) |
→ indica, in media, il costo di ogni unità prodotta |
|
x |
x → quantità prodotta x > 0
|
Cu(x) = |
ax + b |
|
x |
CT(x) = ax + b
x > 0
|
Cu(x) = |
ax2 + bx + c |
|
x |
|
Cu(x) = |
aebx |
|
x |
CT(x) = ax2 + bx
+ c
x > 0
CT(x) = aebx
x > 0
Ricavo totale
Concorrenza
perfetta:
R(x) = px x → quantità
prodotta p → prezzo
Monopolio:
R(x) = p(x) ∙ x p(x) →
si ricava dalla funzione di vendita
Π(x) = R(X) - C(x) → profitto/utile/guadagno
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025