|
|
| |
ALTRI DOCUMENTI
|
|||||
Data una funzione y=f(x) si dice primitiva di y=f(x) una funzione y=F(x) tale che dF(x)=f(x).
L'insieme delle primitive si dice integrale di f(x) in dx
∫f(x) dx = F(x) + C
Si dice equazione differenziale di ordine n una relazione che lega la variabile x, una variabile y=f(x) e le sue derivate fino all'ennesimo ordine.
Forma esplicita:
( y(n) = f(x,y,y ׳ .y(n-1))
Forma implicita:
F(x,y,y ׳ . y(n)) = 0
Si dice integrale generale l'insieme delle soluzioni dell'equazione differenziale. Tali soluzioni differiscono per una costante.
Si dice integrale particolare un integrale che si ottiene attribuendo alle costanti valori arbitrari.
Di dice integrale singolare una soluzione dell'equazione che non fa parte dell'integrale generale.
Si dice serie numerica la sommatoria degli infiniti termini di una successione numerica.
Σ an
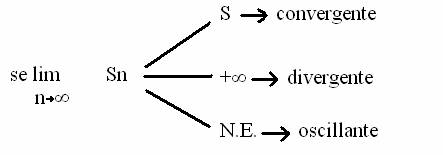
Considerata la successione delle somme parziali, se ne trova il limite con n → +∞. Se Ŕ +∞ la serie Ŕ divergente, se Ŕ un numero la serie Ŕ convergente, e se non esiste la serie Ŕ oscillante.
Considerata
Criterio del rapporto: Ŕ la sommatoria con n=0 e ∞ di an, se il limite con n che tende a ∞ di an+1 fratto an sarÓ >1 allora sarÓ divergente, se risulterÓ =1 sarÓ un caso dubbio e se risulterÓ <1 la serie sarÓ convergente
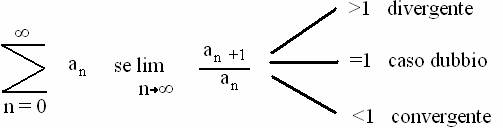
Criterio della radice: Ŕ la sommatoria con n=0 e ∞ di an, se il limite con n che tende a ∞ della radice in base n di an sarÓ >1 allora sarÓ divergente, se risulterÓ =1 sarÓ un caso dubbio e se risulterÓ <1 la serie sarÓ convergente
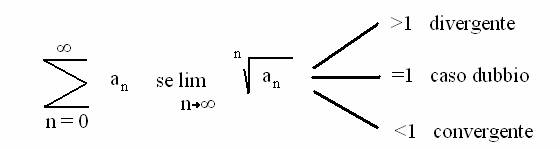
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026