|
|
| |
Calcolare l'integrale doppio
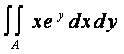
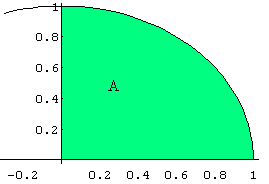
dove A è un insieme così composto
![]()
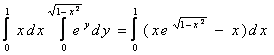
Applico la sostituzione
![]()
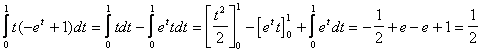
Calcolare l'integrale doppio
![]()
Dove T è 949g67j un insieme così definito
![]()
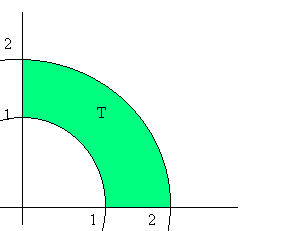
Passaggio a coordinate polari
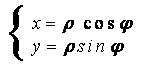
![]()
Dove D è un insieme così definito
![]()
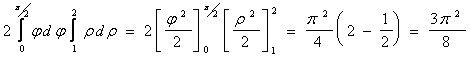
Calcolare l'integrale doppio:
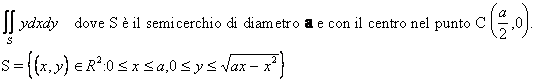
Passaggio alle coordinate polari:

Calcolare l'integrale doppio:
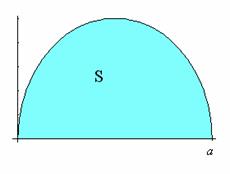
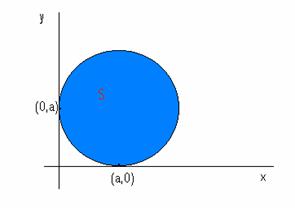
![]() dove S è il cerchio
di raggio a tangente agli assi delle coordinate
dove S è il cerchio
di raggio a tangente agli assi delle coordinate
e situato nel primo quadrante.
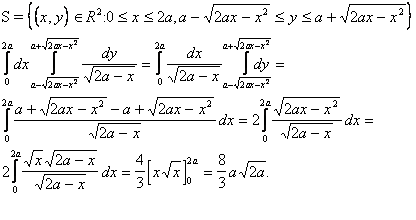
Calcolare l'integrale doppio:
![]()

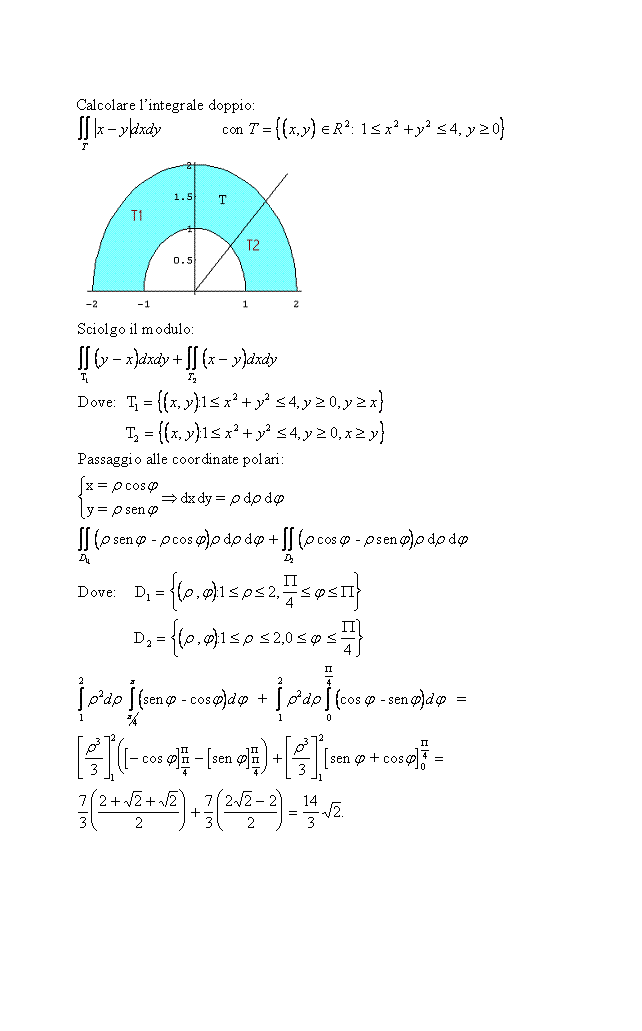
Calcolare l'integrale doppio:
![]()
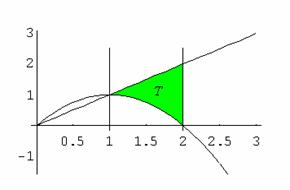

Calcolare l'integrale doppio:
![]()
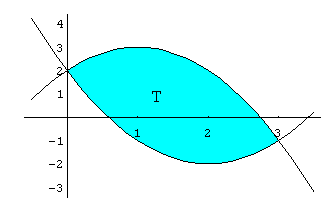
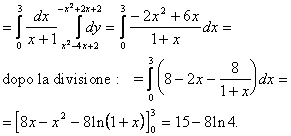
Calcolare l'integrale doppio
![]()
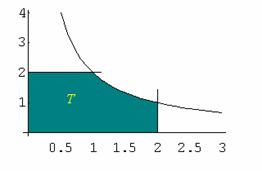

Calcolare l'integrale doppio:
![]()


Calcolare l'integrale doppio:
![]()
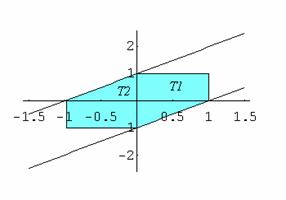

Calcolare l'integrale
![]() T:
T: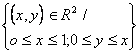
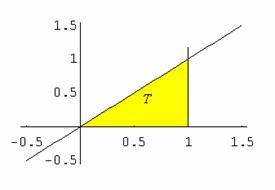

operando la sostituzione:
![]()
l'integrale diventa:
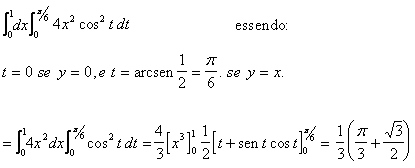
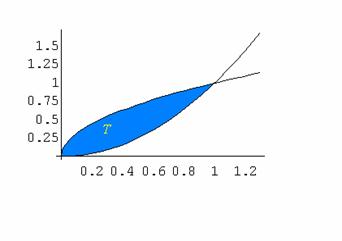
Calcolare l'integrale doppio
![]() Dove T è il semicerchio di raggio 1 e centro
in (1,0) situato nel
Dove T è il semicerchio di raggio 1 e centro
in (1,0) situato nel
semipiano positivo delle y.
Effettuo il passaggio a coordinate polari:
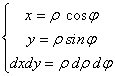
![]() dove
dove ![]()
Riduco rispetto all'asse j

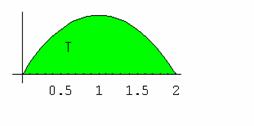
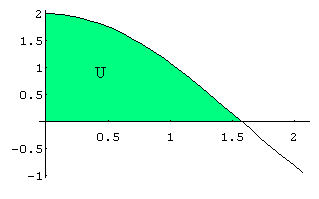
Calcolare l'integrale doppio
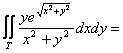 dove T è il quadrante di corona circolare
definito da
dove T è il quadrante di corona circolare
definito da
![]()
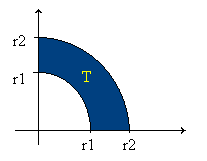
Passaggio alle coordinate polari
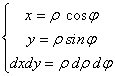
![]() dove
dove ![]()
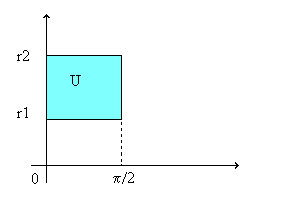
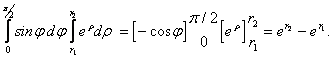
Calcolare l'integrale doppio:
![]()
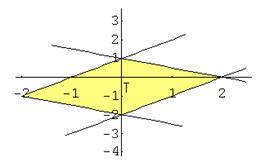

![]()
Calcolare l'integrale
![]()

Integrazione per spilli:

essendo ![]() e
e ![]() con
con ![]() se
se ![]()
L'integrale diventa così:
![]()

Calcolare l'integrale
![]() T:
T: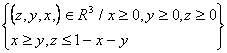
Integrazione per spilli:
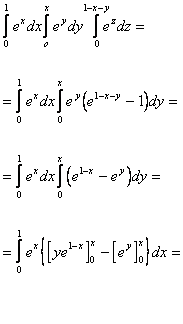
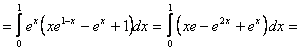
![]()
Calcolare l'integrale triplo
![]() con
con ![]()
T è un dominio normale rispetto al piano xy. Le funzioni a(x,y) e b(x,y) sono due funzioni costanti.
Risolvendo l'integrale triplo mediante il metodo delle spighe (riducendo rispetto al piano xy) otteniamo
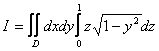 dove D è un dominio base
dove D è un dominio base
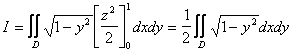
Riducendo rispetto all'asse delle y si ottiene
![]() con
con ![]()
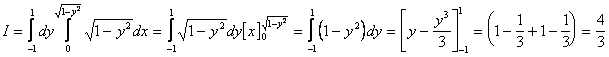

![]()
Passaggio a coordinate sferiche:
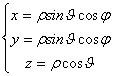
![]()
![]()
![]()

per sostituzione ![]()
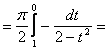 per
sostituzione
per
sostituzione ![]()
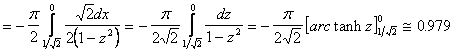
![]()
![]()
![]()
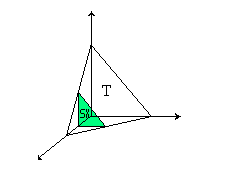

Calcolare l'integrale triplo:
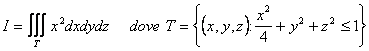
Poiché sia T che l'integrando sono simmetrici
rispetto al piano yz, si può scrivere: ![]() è la parte di T
contenuta nel semispazio delle x positive. Riducendo rispetto al piano yz con
il metodo di integrazione per spighe:
è la parte di T
contenuta nel semispazio delle x positive. Riducendo rispetto al piano yz con
il metodo di integrazione per spighe:
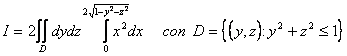
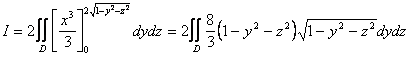
Passo a coordinate polari:
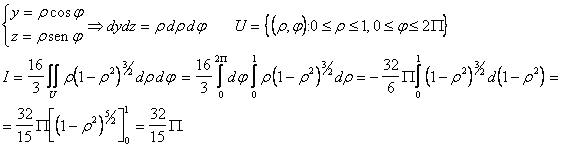
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025