Promemoria per risolvere equazioni e disequazioni esponenziali

matematica

Promemoria per risolvere equazioni e disequazioni esponenziali(1)

Equazioni

Nel caso delle equazioni si possono presentare fondamentalmente 2 casi: i membri sono riducibili a potenze aventi la stessa base o 515h72f ppure no.

es:  = 1/4

Qui 1/4 può essere scritto come ; quindi i due membri verranno ad avere la stessa base. In questo caso basta eguagliare gli esponenti: x - 1 = - 2, ossia x = - 1.

Es: =

Poiché 9 = 3², i membri dell'equazione vengono ad assumere nuovamente la stessa base; eguagliando gli esponenti viene fuori un'equazione di secondo grado in x,

x² - 4, che ha naturalmente come radici 2 e -2.

Es: = 1

L'equazione si può trasformare in = 7º. Eguagliando gli esponenti viene fuori una equazione irrazionale di secondo grado, che non ammette soluzioni nell'ambito dei numeri reali.

Es:  = 0

In questo caso non è possibile ridurre i due membri alla stessa base; tuttavia si può applicare un opportuno cambio di variabile. Ponendo t = l'equazione diventa t² - 9t + 20 = 0, le cui soluzioni sono t = 4 e t = 5; si ottiene = 4, da cui x = 2, e    = 5, da cui x = log .

Disequazioni

Nel caso delle disequazioni, valgono le stesse regole: si cerca di ridurre alla stessa base i due membri, oppure, quando ciò risulta impossibile, cambiare la variabile; tuttavia è necessario prestare particolare attenzione alla base a della potenza.

Nel caso in cui 0 < a < 1, cambia il verso della disequazione;

Nel caso in cui a > 1, il verso rimane invariato.

Es:  > 4

La disequazione si può scrivere come  = 2². Sarà quindi -x - 9 > 2, ossia x > 11

In realtà qualsiasi disequazione del primo tipo (con 0 < a < 1) può essere ricondotta ad una con base maggiore di 1 attraverso piccoli accorgimenti (basta infatti ricordare che 1/a = ); tuttavia è bene ricordare tale distinzione, in quanto nei logaritmi sarà di estrema importanza.

Es:   

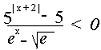
Più complesso apparentemente è questo caso: tuttavia basta risolvere il falso sistema dato dalle equazioni della frazione, ponendo numeratore e denominatore maggiori di zero e prendendo alla fine i valori discordi.

La prima si riduce a | x + 2 | > 1, da cui x > -1 U x < - 3; la seconda, ricordando che  = , si trasforma in x > 1/2. Le radici saranno quindi x < -3 U -1 < x < 1/2.

Conclusioni

Mi sono limitato qui ad esporre le tipologie più frequenti di equazioni e disequazioni esponenziali: tuttavia ne ho tralasciato 1, che richiede la conoscenza dei logaritmi e che comunque, per la sua "pedanteria" ed inutilità, compare raramente nei manuali di matematica. Consiglio vivamente di tenere sotto mano le equazioni e disequazioni irrazionali, fratte e coi valori assoluti, in modo tale da acquisire una certa dimestichezza di calcolo che permetta di affrontare senza problemi questi argomenti.

---