|
|
| |
Le spirali sono alla base del mondo vivente. Il nucleo cellulare è
costituito da una lunga catena a spirale, il DNA, riportante l'intero codice
genetico. Anche la forma di certi organismi può essere a spirale come quella
dell'ammonite, vissuto 300.000.000 555d33f di anni fa.
Archimede ne scrisse un trattato, "Sulle Spirali". anche nella
natura inanimata scopriamo spirali come ad esempio la galassia a spirale.
Le spirali sono anche alla base dei frattali. Ci sono tre tipi comuni di
spirali piane, la più importante delle quali per quanto riguarda i frattali è
la spirale logaritmica. La spirale evoluta è quella che si ottiene srotolando
un gomitolo e tenendo il filo sempre teso; la fine del filo traccerà una
spirale.
Il modo migliore per rappresentarla è con le coordinate polari r e f che costituiscono una valida alternativa alle coordinate cartesiane. r
corrisponde alla distanza del punto P dall'origine (in modulo) e f all'angolo tra OP e l'asse delle x. Da notare che r è sempre maggiore
o uguale a 0 e l'angolo cresce in senso antiorario da 0 e una rotazione
completa aumenta l'angolo di 2p radianti.
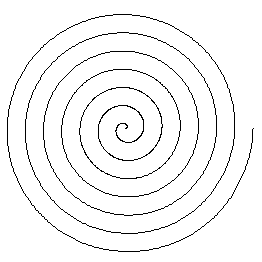
La spirale di Archimede è la più semplice ed è espressa in coordinate polari
con la formula r = af. Tutte le spirali di Archimede sono
simili, differiscono solo per scala.
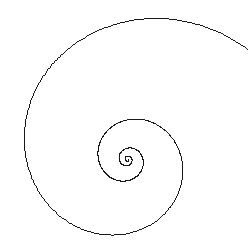
La spirale logaritmica sostituisce la r della spirale di Archimede con il log r, log r = af. Se a è maggiore di 0 la spirale cresce all'infinito, se è minore di 0 procede verso il centro, se a=0 si ha una circonferenza. Il fattore di crescita dipende da f. Si può interpretare come gli spostamenti di una barca attorno ad un faro. Dopo un tratto in linea retta con angolo iniziale b rispetto alla linea che la congiunge con il faro, la nave avrà un angolo di b + a e dovrà aggiustare la rotta. Considerando spostamenti infinitesimi, riducendo a, si arriva ad una spirale indistinguibile da una spirale matematica.
Nel
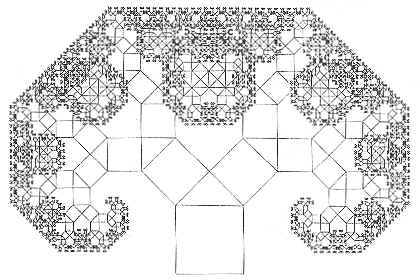
Un quadrato ha un lato in comune con un triangolo rettangolo isoscele, che a sua volta ha gli altri due lati in comune con altri due quadrati e così via. La somma delle aree dei due quadrati più piccoli, per il teorema di Pitagora, è uguale all'area del quadrato iniziale e così anche le aree dei quadrati che si formano nei passaggi successivi, sommate, daranno l'area del primo quadrato. Si può avere un albero asimmetrico semplicemente costruendo un triangolo rettangolo qualsiasi sul lato del primo quadrato.
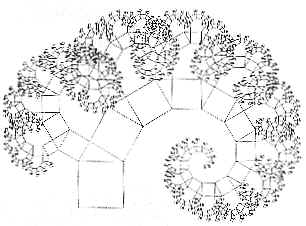
La forma avvolta non è altro che una spirale logaritmica.
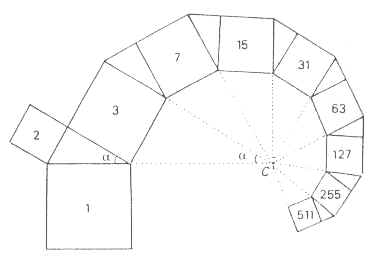
Si possono creare infinite spirali partendo dai quadrati. L'albero di
Pitagora è un buon esempio di frattale matematico. Vi sono anche frattali a
forma di stella, costruiti per esempio con una linea chiusa e successivi
segmenti che si incrociano tutti con lo stesso angolo.
Si può comparare la curva di von Koch con una costa della Bretagna, ma la
natura è creata con casualità. Se si considera la somiglianza statisticamente
si creano frattali più realistici. Per far ciò occorre che ogni parte del
frattale abbia le stesse proprietà statistiche. I metodi basati sul caso sono
detti metodi di Monte Carlo, e in modo più formale stocastici dal verbo
greco che sta per indovinare.
Si può vedere come i frattali siano influenzati da una certa casualità
controllata. Ci sono diversi modi di introdurre il caso nella costruzione dei
frattali e oggi ci sono programmi per computer che possono creare lunghe serie
arbitrarie di numeri casuali. Per esempio si sceglie un numero di 4 cifre e si
eleva al quadrato, poi si tolgono la prima e l'ultima cifra finché non
rimangono ancora 4 numeri, si procede ancora con il quadrato e con il taglio
delle cifre e così via: il risultato è una serie di numeri casuali tra 0 e 9999
che non fallisce test statistici di casualità e nello stesso tempo e stata
creata con una regola precisa.
Tutto deriva dal primo numero, quindi è una sequenza deterministica, ma dà
l'impressione che sia caotica.
Un buon metodo molto pratico per i frattali basato sulla casualità è pensare al
fatto che i frattali sono formati da un numero infinito di punti e che si può
rappresentare solo una frazione di essi, un illusione della loro completezza.
Analizzando ad esempio l'albero di Pitagora scopriamo che sono stati
rappresentati solo i primi 12 passaggi. Introducendo una certa casualità nella
costruzione si potrebbe stabilire di lasciare al caso la decisione di creare
una spirale verso sinistra o verso destra a seconda della disposizione dei lati
dei triangoli rettangoli. Questa introduzione di piccoli disturbi nella costruzione
di frattali rende questi ultimi più simili a oggetti naturali come alberi,
piante, coralli e spugne.
Si è sviluppata quindi una branca della geometria frattale che studia i
cosiddetti frattali biomorfi, cioè simili ad oggetti presenti in natura. I
risultati a volte sono stati stupefacenti. Uno dei frattali biomorfi più
riusciti è la foglia di felce i cui dettagli, detti autosimili, riproducono
sempre la stessa figura.

Attraverso una semplice operazione, la biforcazione di un segmento, si possono ottenere delle "fronde" molto realistiche.

E' interessante notare, parlando in termini informatici, che se si
potesse riuscire ad aumentare il livello di realismo, la quantità di
informazioni (quindi la dimensione di un file) da fornire al computer per
visualizzare una felce su schermo, sarebbe infinitamente minore. Questo uso
della geometria frattale è studiato da diversi anni e viene chiamato IFS
(Iterated Function System).
Robert Brown nel 1828 scoprì che le particelle al microscopio si muovevano in
modo imprevedibile e casuale. Questo è stato chiamato moto browniano. L'idea
della curva di un frattale può aiutare a farsi un'impressione della traiettoria
di un moto browniano. Si deduce che le proprietà statistiche non variano a
seconda della scala. I frattali browniani sono molto naturali. Un paesaggio
lunare potrebbe apparire come la superficie di un frattale: il crateri più
grandi rappresentano la scala maggiore, ma anche con qualsiasi scala minore si
possono vedere crateri; la locazione dei quali è del tutto casuale.

|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025