Es. la variabile X = voto conseguito all'esame

Si osservi che la variabile statistica (i valori che assume e come si distribuiscono sulla popolazione in esame, ovvero la tabella) si indica con la lettera maiuscola; i valori da essa assunti (valori argomentali) si indicano con lettera minuscola.

La variabile puo' essere quantitativa o qualitativa a seconda che i valori che essa assume siano o no "numerici". Cosi' la variabile che descrive la distribuzione del colore degli occhi e' qualitativa, quella che descrive la distribuzione dell' anno di nascita e' quantitativa. Ovviamente si puo' sempre stabilire una corrispondenza tra caratteristica qualitativa e valori numerici (es.: blu = 0, grigio = 1, etc.)

Per ogni valore x_i della variabile ci sara' un sott'insieme della popolazione in esame che la possiede. La frequenza assoluta N_i che corrisponde a tale x_i e' il numero di individui che costituisce tale sott'insieme.

Le frequenze assolute sono numeri interi positivi o nulli. La somma di tutte le frequenze assolute e' pari alla numerosita' della popolazione.

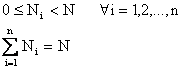
Una variabile statistica e' sempre discreta (i valori argomentali sono sempre in corrispondenza con i numeri naturali) e finita.

Tuttavia in molti casi l'insieme dei valori argomentali puo' non essere definito a priori, come ad esempio nel caso della variabile altezza, ogni individuo della popolazione puo' assumere un valore diverso non definito a priori, a maggior ragione se questa venga espressa al mm o al decimo di mm. In questi casi puo' essere utile creare delle classi, intervalli di ampiezza opportuna: tutti gli individui che presentano un valore appartenente ad una classe, contribuiranno alla frequenza assoluta della stessa.

Es. nel caso della variabile altezza (arrotondata al cm), le classi possono essere .,1.65-1.69,1.70-1.74,1.75-1.79,..

Le classi non devono essere necessarimente della stessa ampiezza, ma vanno fissate caso per caso a seconda del tipo di variabile e delle proprieta' che se ne vogliono mettere in luce.

Esse possono essere rappresentate tramite un unico valore, quale l'estremo superiore, o quello inferiore, oppure il punto medio. Una volta fissata una regola, possono crearsi delle classi nelle quali non rientra nessun individuo, ovvero a frequenza nulla.

Qualora si vogliano confrontare le distribuzioni di variabili dello stesso tipo su popolazioni diverse, con numerosita' diversa, ha senso introdurre il concetto di frequenza relativa di un certo valore x_i, che indicheremo con f_i , pari al rapporto tra la frequenza assoluta e il numero totale di individui della popolazione. Tale frequena dunque rappresenta la proporzione o percentuale degli individui che godono della proprieta' specificata.

La frequenza relativa e' un numero positivo o nullo, la somma delle frequenze relative di tutti i valori argomentali e' pari a 1.

Rappresentazione grafica dei risultati dell'indagine

Per rappresentare i risultati di un indagine statistica si possono riportare i valori argomentali sull'asse delle ascisse di un sistema di coordinate cartesiano e in corrispondenza a ciascun valore, riportare in ordinata la frequenza relativa corrispondente ottenendo un diagramma delle frequenze relative.

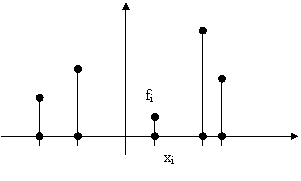
Oppure si puo' utilizzare il diagramma delle frequenze cumulate. In corrispondenza ad ogni x_i, si riporta la somma delle frequenze relative dei valori argomentali minori o uguali a quello considerato. Tra un valore argomentale e un altro il diagramma rimane costante, pari al valore precedente. Ne risulta un diagramma continuo a tratti con una tipica forma di scalinata in salita da sinistra a destra. I punti di discontinuita' sonoi valori argomentali, l'ampiezza della discontinuita' corrisponde alla frequenza relativa del valore argomentale cui si riferisce.

La funzione sara' sempre positiva, crescente perche' somma di quantita' positive o nulle e al massimo pari a 1.

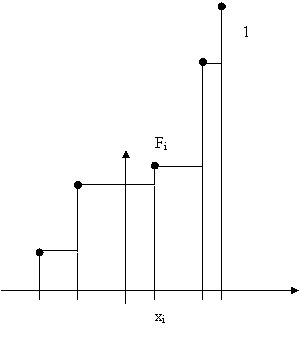
Qualora si suddividano i valori argomentali in classi si ricorre all'istogramma. Per costruirlo si riportano sull'asse delle ascisse le classi in cui si sono suddivisi i valori argomentali, che non necessariamente devono essere di egual ampiezza. In ordinata, per ciascuna classe si riporta il valore della frequenza relativa corrispondente diviso l'ampiezza della classe.

L'area di ciascuna paletta rappresenta la frequenza relativa dell'intervallo cui si riferisce. L'area sottesa dall'istogramma (la somma delle aree delle singole palette), sara' pari a 1.

L'istogramma e' sempre positivo o nullo e il valore in ordinata rappresenta la densita' (costante su ciascun intervallo) di frequenza della variabile statistica.

Il prodotto dell'area di ciascuna paletta per la numerosita' N della popolazione riproduce la frequenza assoluta della classe di valori considerata.

La classe di valori piu' frequenti in una popolazione sara' quella corrispondente alla paletta piu' alta. Va osservato che per variabili continue che in linea di principio possono assumere un qualunque valore reale, cioe' coprire tutto l'asse x, l'istogramma sara' comunque sempre disegnato in modo da coprire solo una parte dell'asse, non si puo' infatti definire l'altezza di una paletta dell'istogramma con una base di lunghezza infinita.

Anche in questo caso si puo' utilizzare la funzione cumulativa di frequenza.

In ascisse si riportano le classi di valori argomentali e per ogni classe, si riporta in ordinata la somma delle frequenze relative delle classi che precedono quella in esame e di quella in esame. Il diagramma risultera' continuo a tratti con la forma di scalinata in salita da sinistra a destra. I punti di discontinuita' sono i rappresentanti della classe di valori argomentali in quello continuo.

L'ampiezza della discontinuita' rappresenta la frequenza relativa della classe.

Osservazione: sia l'istogramma che la funzione cumulativa di frequenza saranno diversi da zero nell'intervallo in cui la variabile statistica e' definita, esse tuttavia possono essere estese a tutto l'asse reale. In particolare l'istogramma sara' zero fuori dall'intervallo di definizione della variabile e la funzione cumulativa sara' zero a sinistra di tale intervallo (cumulo sempre frequenze nulle) e pari a 1 a destra dello stesso (cumulo frequenze nulle a 1).

Media e varianza di X

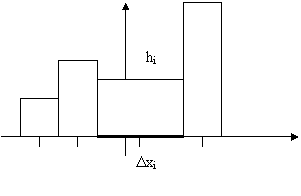
Supponiamo di non avere riordinato i risultati dell'indagine statistica. La media dalla variabile e' data dalla media aritmetica dei valori raccolti, pari cioe' alla somma di tutti i valori argomentali divisa per la numerosita' N della popolazione.

Quando la variabile viene ordinata, i valori argomentali ripetuti, si indicano una sola volta nella prima riga della variabile statistica, mentre il numero di volte che si presentano (frequenza assoluta), si registra in corrispondenza nella seconda riga.

L'espressione della media in tal caso diventa:

ovvero una media aritmetica dei valori argomentali, presi una sola volta, pesati (moltiplicati) ciascuno con la propria frequenza assoluta.

Ricordando poi la definizione di frequenza relativa si arriva alla seguente ulteriore espressione:

Per molte distribuzioni la media da' una informazione su dove (sull'asse delle x) la variabile statistica ha frequenze che tendono ad addensarsi. Essa si dice un indice di posizione. La media assume valori compresi nell'intervallo dei valori argomentali:

Per avere maggiore informazione sulla dispersione della distribuzione della frequenza intorno alla media si calcola l'indice di varianza. Nel caso di variabile non ordinata e' la media aritmetica delle differenze (scarti) al quadrato di ciascun valore argomentale dalla media.

e per variabili ordinate sara' data da

Tale indice da' una informazione sulla variabilita' dei valori argomentali rispetto alla media: se e' alta ci saranno valori argomentali distanti dalla media con frequenza elevata, nel caso opposto, ci sara' un'alta frequenza concentrata intorno alla media.

La varianza e' un valore positivo o nullo e minore o uguale al quadrato della distanza massima dalla media.