|
|
| |
INTEGRALI
Per comprendere il significato dell'integrale definito e il metodo con cui questo viene calcolato, partiamo da un esempio semplice, preso dalla fisica.
Consideriamo un punto materiale che si muove lungo una retta (asse x) con velocità costante. Il grafico velocità-tempo è rappresentato in figura 1.
Figura 1
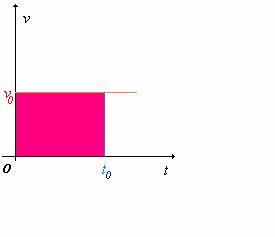
La distanza percorsa nell'i 454f53e ntervallo di tempo da t=0 a t=t0 è data dall'area (in rosso) nella figura, cioè x=v0t. Se ora la velocità è una funzione variabile del tempo, rappresentata da una curva generica, come mostrato ad esempio in figura 2, lo spostamento del corpo nell'intervallo temporale Dt è dato, analogamente, dall'area (in blu) sottesa dalla curva v(t).
Figura 2
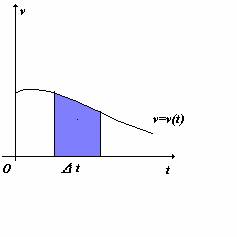
Le basi teoriche che consentono il calcolo di tale area, e quindi, nell'esempio considerato, dello spostamento del punto materiale, costituiscono il calcolo integrale.
Consideriamo ora una generica funzione y = f(x) definita in un intervallo [a,b] e ivi continua. Per determinare l'area sottesa dalla funzione si suddivide l'intervallo [a,b] in n sottointervalli di ampiezza Dxi = xi - xi-1. In ciascuno di questi intervalli la funzione ammetterà un valore massimo f(M) e un valore minimo f(m).
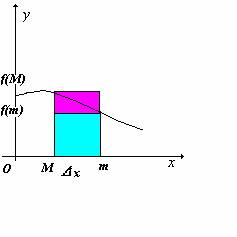
Se consideriamo tutti gli n sottointervalli in cui abbiamo suddiviso l'intervallo [a,b] otteniamo il grafico di figura 4 .
Figura 4
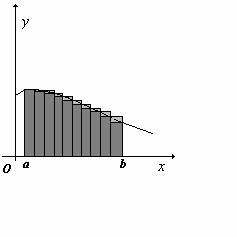
In ciascun intervallo la funzione ammette un valore massimo f(Mi) e un valore minimo f(mi).
Consideriamo ora i due insiemi di rettangoli: quelli con base Dxi e altezza f(mi) e quelli con la stessa base e altezza f(Mi). I primi risultano inscritti, i secondi circoscritti al grafico rappresentante la funzione considerata.
Le somme delle aree dei rettangoli inscritti e circoscritti sono rispettivamente:
s = ![]()
S = ![]()
L'area A sottesa dalla funzione (detta area del trapezoide) è compresa fra le due: s A S
Se esiste ed è finito il limite per Dxi delle sommatorie precedenti, la funzione f si dice integrabile e l'area A del trapezoide da essa sotteso vale:
![]() = A =
= A = ![]() .
.
L'operazione appena definita viene indicata con:
![]()
e prende il nome di integrale definito.
Il calcolo di tale area viene ricondotto
alla determinazione di una funzione F(x detta funzione
primitiva della f(x), tale che la derivata di F sia esattamente la funzione f (ovvero F'=f). In tal modo l'area è data da: ![]() . Chiaramente, esisteranno infinite primitive della funzione f , che differiscono tra loro per una
costante A (numero!), poichè la derivata di una costante vale zero, e quindi
que funzioni F(x) e F(x)+A hanno uguale derivata. La
ricerca di una funzione primitiva, operazione inversa della derivazione, prende
il nome di integrazione indefinita.
. Chiaramente, esisteranno infinite primitive della funzione f , che differiscono tra loro per una
costante A (numero!), poichè la derivata di una costante vale zero, e quindi
que funzioni F(x) e F(x)+A hanno uguale derivata. La
ricerca di una funzione primitiva, operazione inversa della derivazione, prende
il nome di integrazione indefinita.
Notiamo anche che solo se f(x) è positiva, il suo integrale
definito tra a e b , che si indica con: ![]() coincide con l'area
del dominio limitato dall'asse x,
dalla funzione y=f(x) e dalle rette x=a e x=b.
coincide con l'area
del dominio limitato dall'asse x,
dalla funzione y=f(x) e dalle rette x=a e x=b.
Diamo qui di seguito alcune regole di integrazione e le primitive di alcune funzioni.
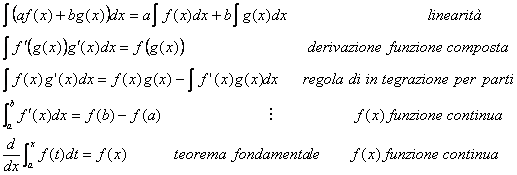
INTEGRALI ELEMENTARI (indichiamo una primitiva)
![]() se r
se r
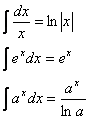

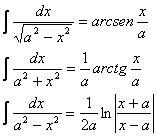
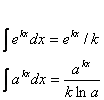
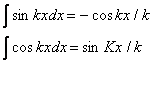
![]() se r
se r
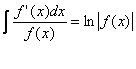
INTEGRALI TRIGONOMETRICI
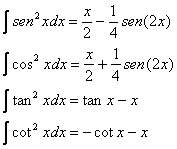
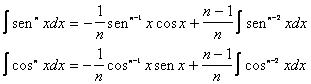
INTEGRALI CONTENENTI EXP(X) O LN(X)

INTEGRALI DI FUNZIONI TRIGONOMETRICHE INVERSE
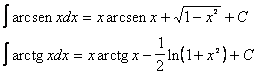
INTEGRALI
CONTENENTI ![]() e
e ![]()
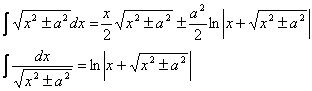

INTEGRALI DI FUNZIONI IPERBOLICHE
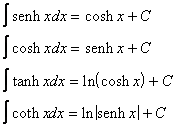

INTEGRALI VARI

![]() se n
se n
![]() se n
se n
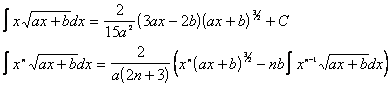
Affrontiamo ora il secondo problema proposto: quello del
calcolo della lunghezza di una linea curva. Anche in questo caso (vedi figura
5) suddividiamo l'intervallo chiuso [a,b]
in n sottointervalli mediante i punti
a = t0 < t1<...<tn
= b in modo chi i punti ri = r(ti) suddividono
l'arco considerato in n archi. Se si usa la lunghezza della corda |ri - ri-1| come
approssimazione dell'arco i-esimo la somma
sn = ![]() approssima la
lunghezza della curva considerata. Moltiplichiamo e dividiamo per l'intervallo Dt (che sarà ad esempio la distanza tra due valori ti-ti-1
del parametro usato per la suddivisione) ciascun elemento di questa somma:
approssima la
lunghezza della curva considerata. Moltiplichiamo e dividiamo per l'intervallo Dt (che sarà ad esempio la distanza tra due valori ti-ti-1
del parametro usato per la suddivisione) ciascun elemento di questa somma: ![]()
Figura 5
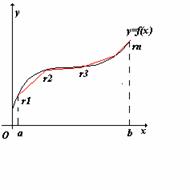
Si può mostrare che la lunghezza della curva considerata è data da
s = ![]() .
.
Nel caso in cui r(t) rappresenti la legge oraria di un punto materiale, dr/dt rappresenta la velocità scalare del punto stesso, e quindi la lunghezza della traiettoria è data prorpio dall'integrale della velocitàscalare rispetto al tempo.
Possiamo scrivere quindi
![]()
È da notare che la lunghezza della curva risulta indipendente dalla particolare parametrizzazione scelta per la linea C.
Se la rappresentazione parametrica della
curva è: ![]()
allora ![]()
se invece la curva è data in forma cartesiana: y=y(x),
utilizzando come parametro la variabile x, si ha: ![]()
Nel caso in cui la curva sia rappresentata in forma polare: r=r(q
possiamo considerare la seguente
parametrizzazione: 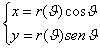
da cui si ricava ![]()
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025