|
|
| |
LE DISTRIBUZIONI DOPPIE
In questa lezione presenteremo le distribuzioni doppie ed alcune loro importanti caratteristiche come la costruzione della distribuzione di frequenze e le distribuzioni marginali. Impareremo, inoltre, alcuni termini propri delle distribuzioni secondo due caratteri.
Supponiamo di voler rilevare su un collettivo di studenti universitari due caratteri: l'altezza ed il peso. Ovviamente mi troverò davanti ad una distribuzione unitaria come la seguente:
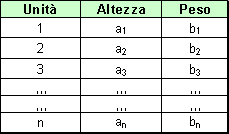
Sui nostri n studenti abbiamo rilevato due caratteri, il peso e l'altezza ( per facilità ho preso caratteri quantitativi ); quindi ad ogni unità corrispondono due numeri. Come si è visto nelle distri 515e49f buzioni semplici, è utile passare dalla distribuzione unitaria ad una distribuzione di frequenze. Questo passaggio è un po' più delicato di quanto visto nelle distribuzioni semplici in quanto non dobbiamo semplicemente contare quante volte una modalità si presenta nella popolazione (quindi calcolarne la frequenza assoluta), ma dobbiamo vedere quante volte una data coppia (altezza, peso) si presenta nella popolazione.
Vediamo un esempio numerico considerando la seguente distribuzione:
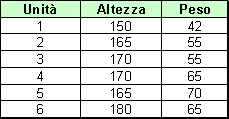

Quella appena costruita è una tabella doppia di frequenze: vediamo in particolare quali sono le sue parti. Le due aree colorate in rosa ci indicano quali sono i caratteri presi in considerazione ( in questo caso abbiamo altezza e peso ); nelle due aree gialline troviamo le modalità con cui si presentano i suddetti caratteri, in particolare l'area posta sotto il carattere altezza è indicata con il termine testata ed indica le modalità con cui si è presentata l'altezza; la colonna giallina accanto al peso è detta colonna madre ed indica le modalità assunte dal peso. L'area in verde ci dice come peso e altezza si accoppiano in ogni unità, ovvero, in corrispondenza delle modalità 42 e 150 troviamo un 1, questo indica che nel nostro collettivo c'è una persona alta 150 cm e che pesa 42 Kg. Così via per tutte le coppie di modalità.
Nelle due aree celesti troviamo i totali per colonna (area in basso) e per riga (area in alto); queste due distribuzioni sono molto importanti in quanto ci permettono di passare dalla distribuzione doppia del peso e dell'altezza alle distribuzioni marginali del peso, separato dall'altezza. Infatti prendendo in considerazione la colonna madre e la colonna del totale abbiamo la seguente distribuzione marginale del peso:
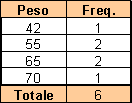
Ed analogamente troviamo la distribuzione marginale delle altezze:
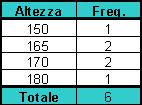
Le distribuzioni marginali viste non sono altro che distribuzioni semplici.
Vediamo quali altre informazioni possiamo desumere da una distribuzione doppia: ad esempio, prendendo la colonna madre ed un'altra colonna qualsiasi della distribuzione abbiamo la distribuzione parziale della distribuzione doppia.
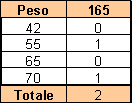
Questa nuova tabella ci dice la distribuzione del peso fra le persone alte 165 cm.
In generale daremo alle distribuzioni doppie la seguente forma:
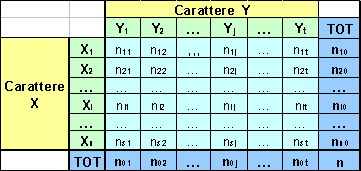
La generica Yj indica una modalità del carattere Y, analogamente la generica Xi indica una modalità del carattere X; il generico elemento n i j indica la frequenza delle unità che presentano modalità Xi e Yj . Questa appena vista è la distribuzione delle frequenze assolute, per passare alla distribuzione delle frequenze relative basta dividere tutto per n:
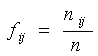
Per ulteriori approfondimenti e per il calcolo di importanti misure vedere il documento " Distribuzioni doppie "
In questa lezione abbiamo presentato le distribuzioni secondo due caratteri, chiamate distribuzioni doppie; abbiamo visto come si costruisce una tabella doppia e come si costruiscono distribuzioni marginali e parziali secondo un solo carattere o una sola modalità.
Domande
Glossario
A
AREOGRAMMA
Particolare tipo di rappresentazione grafica in cui la frequenza o la quantità di una data modalità vengono rappresentate attraverso l'area di una figura piana. In particolare tale area dovrà essere proporzionale alla frequenza rappresentata.
AMPIEZZA DELLA CLASSE
L'ampiezza di una data classe si calcola facendo la differenza fra l'estremo superiore e quello inferiore della classe in esame.
C
CAMPIONE
Parte della popolazione costruita in modo tale da rappresentare al meglio la popolazione da cui viene estratto. Lo scopo della costruzione di un campione è quello di lavorare su un collettivo più piccolo della popolazione, per poi espandere i risultati ottenuti a tutta la popolazione.
CAMPO DI VARIAZIONE
Il campo di variazione è una misura della variabilità di una distribuzione e si ottiene calcolando la differenza fra il termine più grande e quello più piccolo della distribuzione.
CARATTERE
In ogni ricerca statistica studiamo una o più caratteristiche delle unità rilevate; queste caratteristiche vengono definite con il termine carattere. Il carattere si manifesta nelle unità attraverso varie modalità.
CENSIMENTO
Rilevazione generale della popolazione di un paese; il censimento si effettua ogni 10 anni e va a rilevare alcune caratteristiche di tutta la popolazione.
CENTRO
Data una distanza, il centro di una distribuzione è il valore che, rispetto alla distanza considerata, rappresenta al meglio la popolazione
CLASSI
Le classi sono il frutto della divisione delle modalità di un carattere in gruppi. In particolare, le modalità di un carattere come il peso o l'altezza, per semplificare il lavoro, possono essere raggruppate insieme, creando un'unica modalità, generalmente rappresentata dal valore centrale della classe.
CONCENTRAZIONE
Attributo che si dà ad un carattere quantitativo trasferibile. Si dice che, in una distribuzione la concentrazione è massima quando tutto l'ammontare del carattere si trova in una sola unità; al contrario, si dice che un carattere è equidistribuito quando l'ammontare è equamente diviso fra tutte le unità della popolazione. La concentrazione rientra nelle misure della variabilità di una distribuzione.
COGRADUAZIONE
La tabella di cograduazione si calcola in ambito di dissomiglianza e serve per gestire più facilmente i dati cograduati. In particolare ci dice che modalità presentano i dati cograduati.
COGRADUATI (DATI)
Definiamo termini cograduati di una distribuzione quei termini che occupano lo stesso posto nella graduatoria dei termini di una distribuzione.
D
DATO ANOMALO
Un dato è definito anomalo quando è molto diverso dagli altri dati della distribuzione. Tale diversità può attribuirsi ad errore (di rilevazione o inserimento) o all'inizio di una nuova fase del fenomeno.
DETERMINAZIONE (indice di)
Visto nell'ambito della regressione, l'indice r2 indica la bontà di accostamento di ciascuna delle rette di regressione ai dati osservati. Abbiamo che
![]()
Se r2 = 0 allora le due rette di regressione coincidono con gli assi cartesiani (con origine posta nel baricentro). Se r2 = 1 allora i punti osservati sono allineati e le due rette di regressione sono sovrapposte. In altre parole, tanto più l'indice di determinazione è vicino a 1 tanto più le rette descriveranno meglio la distribuzione osservata.
DEVIANZA TOTALE
In ambito di regressione, definiamo devianza totale la distanza fra ogni valore osservato Yj e la media Y. E' valida la seguente relazione: DEV. TOT. = DEV. REG. + DEV. RES
DEVIANZA DI REGRESSIONE
In ambito di regressione è la distanza fra i valori teorici Y*j e la media Y. E' anche chiamata devianza spiegata dalla regressione.
DEVIANZA RESIDUA
In ambito di regressione, indica la distanza fra la distribuzione osservata e la distribuzione teorica rappresentata dai punti della retta di regressione.
DIPENDENZA IN MEDIA
Data una distribuzione secondo due caratteri, diciamo che se Y è indipendente in media da X allora le distribuzioni parziali secondo il carattere Y hanno la stessa media aritmetica. Ricordiamo che una situazione di connessione nulla implica indipendenza in media. Un indice di dipendenza in media è quello proposto da Pearson (vedi lezioni)
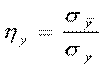
che assume valore 1 nel caso di dipendenza perfetta di Y da X; assume invece valore 0 nel caso di indipendenza in media.
M
MODALITA'
Ogni carattere si presenta nelle unità attraverso delle modalità. Ad esempio il carattere sesso si presenta con le modalità maschio e femmina.
V
VALORE CENTRALE DI UNA CLASSE
Il valore centrale di una classe è la misura che più frequentemente si usa nelle elaborazioni di caratteri divisi in classi. Si trova sommando gli estremi della classe e dividendo il risultato per 2.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025