Derivata - Integrale

al tendere di t a to. [La derivata di un vettore ha le stesse proprietà della derivata di una funzione scalare; in particolare alla derivata del prodotto f(t) · v(t), con f(t) funzione scalare, si applicano le consuete regole di derivazione.]

Consideriamo  una funzione di una variabile y = f(x). Diamo a x, a partire da un valore determinato, un incremento h; ne risulta per la funzione un corrispondente incremento k = f(x + h)f(x).

Se il rapporto k/h tende a un limite finito quando h tende a 0, secondo una legge qualunque, questo limite si chiama derivata della funzione f(x) per il valore di x considerato. Si rappresenta la derivata con la notazione y'o f'(x) o dy/dx. Perché una funzione ammetta derivata per un valore di x, è necessario che essa sia continua per quel valore della variabile. Allora k tende a 0, al tendere a 0 di h. Questa condizione necessaria non è però sufficiente ad assicurare l'esistenza della derivata; perché ciò avvenga è inoltre necessario che il rapporto k/h, che si presenta sotto la forma 0/0, abbia un limite finito e determinato. Si può dare della derivata una rappresentazione geometrica. Consideriamo la curva la cui equazione riferita a un sistema di assi qualunque sia y = f(x). Siano M e M' i punti della curva aventi per coordinate rispettivamente x, y e x + h, y + k. La corda M M' ha per coefficiente angolare il rapporto k/h. Facendo tendere h a 0 la corda M M'ha per posizione limite la tangente M T alla curva nel punto M, e la derivata, per il valore di x considerato, è rappresentata dal coefficiente angolare della tangente M T.

Derivate successive. y' = f'(x) è in generale una funzione di x. Se si considera la derivata di f'(x) si ottiene la derivata seconda di f(x), che si rappresenta con il simbolo y'' o f''(x) o d²y/dx². Prendendo la derivata di f''(x), si ottiene la derivata terza di f(x), y''' o f'''(x) o d³y/dx³; ecc.

Derivata di una somma, di un prodotto, di un quoziente, di una potenza. Siano u, v, w funzioni di x derivabili, si ha:

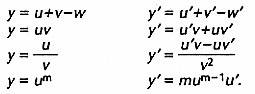
Esempi. Derivate di alcune funzioni elementari.

Integrale

Integrale definito di una funzione f(x) o di un differenziale f(x)dx nell'intervallo (a, b), valore numerico espresso mediante la notazione , che l'operazione detta di integrazione permette di calcolare per l'intervallo (a, b) quando la funzione f(x) sia integrabile in questo intervallo. (Questo intervallo è chiamato intervallo d'integrazione. Le sue estremità sono i limiti dell'integrale e x è la variabile di integrazione.) Integrale indefinito o funzione primitiva di una funzione f(x), ogni funzione F(x) la cui derivata è f(x). (Essa è determinata a meno di una costante, detta costante d'integrazione.)

L'integrale  indefinito di alcune funzioni elementari si può esprimere a sua volta mediante funzioni elementari.

v Integrale di un'equazione differenziale

Data  un'equazione differenziale alle derivate ordinarie di ordine n, il suo integrale è la funzione che la rende soddisfatta: tale funzione è così chiamata perché la sua ricerca comporta generalmente operazioni di integrazione. Si chiama integrale generale una funzione che soddisfa l'equazione e dipende da n costanti arbitrarie, tali che se ne possa disporre in modo da imporre a essa e alle sue prime n-1 derivate di assumere, in un dato punto, valori arbitrariamente prefissati; l'integrale particolare non è che l'integrale generale in cui siano fissate delle costanti; si chiama invece integrale singolare una soluzione che non può dedursi dall'integrale generale dando particolari valori alle costanti d'integrazione. Le equazioni differenziali più semplici sono quelle lineari omogenee a coefficienti costanti; in questo caso l'integrale generale si può esprimere mediante le radici di una opportuna equazione algebrica detta equazione caratteristica. Precisamente l'integrale generale dell'equazione

y(n)a + y(n1) a + ... y´an + yan

dove a , a , ..., an sono delle costanti, si può esprimere nella forma

y(x) = C er1x + C er2x + ... Cnernx

dove C , C , ..., Cn sono le n costanti arbitrarie e r , r , ..., rn sono le n radici (supposte distinte) dell'equazione caratteristica

rna + rn a + ... r an + an

Quando alcune radici di queste equazioni coincidono, l'integrale generale assume una forma lievemente differente.

Nel caso di equazioni differenziali alle derivate parziali, nell'integrale generale devono essere assegnate non costanti ma funzioni arbitrarie, in base a condizioni imposte a priori alla soluzione (condizioni al contorno).

Limite

Numero o ente di natura più generale associato a una funzione o a una successione mediante il procedimento di passaggio al limite. Limite superiore o inferiore (di una funzione o di un insieme di numeri reali), termine usato talvolta per indicare rispettivamente l'estremosuperiore o inferiore. Limiti di integrazione, estremi dell'intervallo di integrazione di un integrale di linea.

Il  concetto di limite è il principio fondamentale di tutta l'analisi infinitesimale; su di esso si fondano il calcolo differenziale e integrale e la definizione rigorosa dei principali concetti dell'analisi e di molti altri rami della matematica (per es. la definizione di derivata, integrale, continuità, ecc.). Il concetto di limite si trova già, in forma embrionale, in Eudosso di Cnido e soprattutto in Archimede (il metodo d'esaustionepuò considerarsi come la prima formulazione approssimativa del passaggio al limite). In epoca moderna la prima definizione di limite si ritrova nei Principia di Newton (1687), ma l'idea fondamentale è oscurata da complicati artifici fondati su modelli dinamici di punti in movimento. La prima chiara esposizione puramente matematica è dovuta a Cauchy (1821); tale formulazione è rimasta finora sostanzialmente immutata. 

v Limite di una funzione

Data  una funzione f(x) di una variabile reale x, definita in un intervallo (a, b), si dice che f(x) fende al limite l per x tendente a x (simb.:

se per ogni numero positivo arbitrario e si può trovare un numero d funzione di e tale che per ogni x contenuto nell'intorno

|x x < e

di x valga la relazione f(x) l < e

In altri termini si può dire che f(x) tende al limite l per x tendente a x (simb.: xDx ) quando i valori assunti da f(x) in un intorno sufficientemente piccolo di x differiscono da l di una quantità arbitrariamente piccola. Il procedimento utilizzato per determinare l è noto come passaggio al limite. È importante notare che la precedente definizione di limite è indipendente dal valore assunto da f(x) nel punto x ; anzi, può succedere che, benché il limite esista, la funzione f(x) non sia definita in x ; nel caso particolare in cui risulta f(x ) = l, la funzione si dice continua in x . La definizione di limite si può facilmente estendere al caso in cui x o l divengono infiniti: se, per es., in un intorno sufficientemente piccolo di x i valori di f(x) possono essere resi maggiori, in valore assoluto, di qualsiasi numero prefissato, allora si dice che f(x) tende a infinito per xDx (simb.:

È da notare che non sempre esiste il limite così definito; in questo caso è possibile talvolta definire un limite destro l o un limite sinistro l introdotti nella stessa maniera di l, considerando però unicamente gli intorni destri o quelli sinistri di x (in simboli:

La nozione di limite si può ulteriormente estendere anche a funzioni di più variabili f(x , x ,... xn): si può ancora usare la definizione precedente purché si definisca adeguatamente la nozione di intorno di un'ennupla di numeri; a tal fine si ricorre alla rappresentazione di tale ennupla con un punto P di uno spazio euclideo a n dimensioni. In questo caso la notazione sta a indicare che i due valori assunti da f in tutti i punti P contenuti in una sfera di centro P e raggio sufficientemente piccolo differiscono di poco quanto si vuole dal numero l. Il concetto di limite si può altresì generalizzare anche a funzioni  f(P) i cui valori non sono numeri, ma elementi di uno spazio metrico o topologico o di natura ancor più generale.

v Limite di una successione o di una serie

Si dice che una successione di numeri a , a ,... an . tende al limite l per n tendente all'infinito (simb.:) se, dato un e positivo a piacere esiste un intero n tale che per ogni n>n si abbia

an l < e

Sarebbe facile dimostrare che la nozione di limite per una successione è un caso particolare di quella definita per le funzioni. Il limite di una serie a + a +...+ an . (detto più spesso somma della serie) si riconduce al limite della successione costruita con le sue ridotte S , S ,... Sn,..., dove Sn rappresenta la somma dei primi n termini della serie.

v Operazioni algebriche sui limiti

L'operazione  di passaggio al limite può commutare talvolta con le quattro operazioni fondamentali dell'algebra: nel caso in cui i due limiti e esistano e siano finiti e non nulli, si ha:

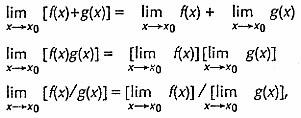
se invece l o l sono nulli o infiniti può succedere che tali proprietà non siano più valide e allora per il calcolo di tali limiti si ricorre ad altri procedimenti come ad es. la regola di L'Hospital.