MEDIE E INDICI DI POSIZIONE

1 MODA o norma (Mo)

La moda è quella modalità cui corrisponde la massima frequenza (fenomeno unimodale). Se a due o più modalità sono associate le stesse più elevate frequenze il fenomeno si definisce bimodale o plurimodale.

1.1 Campo di esistenza della moda

La moda può essere determinata per qualsiasi fenomeno, anche sconnesso.

1.2 Calcolo della moda

La moda di una mutabile s 616d37g tatistica o di una variabile statistica discreta si identifica con una modalità.

La moda di una variabile statistica continua (la cui distribuzione è espressa in classi) si identifica col valore centrale della classe modale (la classe cui corrisponde la massima frequenza).

Se le classi hanno diverse ampiezze, le rispettive frequenze, assolute o relative, non sono confrontabili tra loro. In questo caso la moda corrisponde al valore centrale della classe modale con la massima frequenza ridotta. Per calcolare le frequenze ridotte o specifiche (frequenze afferenti a classi unitarie) occorre dividere ciascuna frequenza assoluta per la corrispondente ampiezza della classe.

2 MEDIANA (Me)

2.1 Campo di esistenza della mediana

La mediana può essere determinata per qualsiasi fenomeno ad eccezione di quello qualitativo sconnesso e, quando P₁ e P₂ corrispondono a modalità diverse, di quello qualitativo rettilineo.

2.2 Definizione e calcolo della mediana

Poste le n osservazioni x_i in ordine non decrescente, si definisce genericamente mediana la modalità o la classe che corrisponde all'intensità o alla frequenza relativa che occupa la posizione centrale.

Se n è dispari la mediana è la modalità o la classe che corrisponde alla posizione , che divide la distribuzione in due parti uguali, lasciando alla sua sinistra e alla sua destra un numero di unità uguale a .

Se n è pari la mediana è la modalità o la classe che corrisponde alle posizioni e che lasciano a destra e sinistra lo stesso numero di unità.

Nel caso di fenomeni qualitativi rettilinei con n pari, se le due posizioni P₁ e P₂ corrispondono a due modalità diverse la mediana si preferisce non determinarla.

Nel caso di fenomeni quantitativi discreti con n pari, se le due posizioni P₁ e P₂ corrispondono a due modalità diverse la mediana è data dalla semisomma delle due modalità.

Nel caso di fenomeni quantitativi continui (distribuzione di frequenze per classi), la mediana si può calcolare secondo due criteri:

1° criterio: mediana pari al valore coincidente col valore centrale o medio della classe (il criterio si basa sull'assunzione che le unità rilevate in una certa classe abbiano tutte lo stesso valore coincidente col valore centrale o medio della classe);

2° criterio (consiste nel supporre che i valori all'interno della classe siano ripartiti uniformemente):

con n dispari: mediana pari a

dove

h_i è il limite inferiore della classe mediana

P è la posizione della mediana

N_i-1 è la frequenza cumulata della classe precedente quella mediana

n_i è la frequenza assoluta della classe mediana

a_i è l'ampiezza della classe mediana

con n pari: si calcolano i due valori mediani applicando la formula sopra vista in caso di n dispari e si determina la mediana come semisomma dei due valori.

Nel particolare caso di rilevazioni di n termini x₁, x₂ ... x_n disposti in ordine non decrescente, la mediana è il valore del termine centrale se n è dispari, ovvero, la media aritmetica dei valori dei due termini centrali se n è pari.

In entrambi i casi, il numero dei termini che precedono la mediana è uguale al numero dei termini che la seguono. La mediana divide pertanto la distribuzione in due parti uguali.

Es. Le quantità di un dato prodotto vendute a 7 clienti nel 2002 sono state le seguenti (in quintali)

72 82 84 98 105 137

la vendita mediana per cliente è stata di 84 quintali

Es. quantità di un dato prodotto vendute a 8 clienti nel 2002 sono state le seguenti (in quintali)

18 36 72 82 84 98 105 137

la vendita mediana per cliente è stata di 83 quintali (82 + 84)/2

3 LE MEDIE POTENZIATE

Si definisce media potenziata di ordine r (o media di potenze) di una variabile statistica X l'espressione:

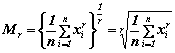
o, nel caso di ponderazione, con la presenza di frequenze assolute n_i o relative f_i, le espressioni:

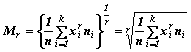e

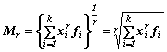
Si definiscono momenti di ordine r della variabile statistica le potenze r-esime delle medie potenziate di ordine r : o, in forma ponderata e

Le proprietà dei momenti di ordine r (per i quali non valgono le proprietà di internalità, moltiplicativa e di monotonicità proprie delle medie) sono le seguenti:

-

-

3.1 MEDIA ARITMETICA

La media aritmetica è una media potenziata di ordine r=1.

Si definisce media aritmetica semplice di una variabile statistica l'espressione  

o, nel caso di ponderazione, vale a dire con la presenza di frequenze assolute n_i > 1 o relative f_i > 1/n, le espressioni    o

La media aritmetica coincide con il valore centrale di una progressione aritmetica con un numero dispari di termini o con la media aritmetica dei due valori centrali se il numero di termini è pari.

Proprietà della media aritmetica

a) la somma algebrica degli scarti dei valori x_i dalla loro media aritmetica è nulla;

b) la somma dei quadrati degli scarti dei valori x_i dalla loro media aritmetica è minima rispetto agli scarti da qualsiasi altro valore a

c) se i valori x_i vengono trasformati nei valori y_i=a+bx_i, la media aritmetica subisce la stessa trasformazione, ossia   .

Ne discende quindi che, nota la trasformazione lineare e la media della variabile X, è possibile determinare direttamente la media della variabile Y senza operare i calcoli previsti delle formule della media aritmetica semplice o ponderata.

Analogamente vale la relazione inversa

Teoremi della media aritmetica

I teorema:    la media aritmetica di un miscuglio di k gruppi (o sottopopolazioni), per ciascuno dei quali è gia noto il valore della media aritmetica, è uguale alla media aritmetica ponderata delle medie dei singoli gruppi.

II teorema:   la media aritmetica della somma (o della differenza) di due o più variabili è uguale alla somma (o alla differenza) della media aritmetica delle singole variabili M(X + Y) = M(X) + M(Y).

3.2 MEDIA GEOMETRICA

La media geometrica è una media potenziata di ordine 0.

Si definisce media geometrica semplice di una variabile statistica l'espressione   (a)

o, nel caso di ponderazione, vale a dire con la presenza di frequenze assolute n_i > 1 o relative f_i > 1/n, le espressioni    (b) o (c)

Per calcolare la media geometrica si ricorre solitamente ai logaritmi per cui le espressioni sopra viste si trasformano rispettivamente nelle seguenti:

(aa)

(bb)

(cc)

Naturalmente la media geometrica esiste solo per valori positivi della variabile e, per determinarla, si deve ricorrere all'antilogaritmo.

Proprietà della media geometrica

Come si vede nella espressione (aa), il logaritmo della media geometrica è uguale alla media aritmetica dei logaritmi delle modalità x_i. Ne discende che per esso valgono tutte le proprietà formali della media aritmetica, ossia:

a) la somma algebrica degli scarti dei logaritmi dei valori x_i dal logaritmo della loro media geometrica è nulla;

b) la somma dei quadrati degli scarti dei logaritmi dei valori x_i dal logaritmo della loro media geometrica è minima rispetto agli scarti da qualsiasi altro valore a. Inoltre

c) la media geometrica dei rapporti y_i/x_i coincide con il rapporto della media geometrica dei numeratori e dei denominatori

La media geometrica coincide con il valore centrale di una progressione geometrica con un numero dispari di termini o con la media geometrica dei due valori centrali se il numero di termini è pari.

3.3 MEDIA ARMONICA

La media armonica è una media potenziata di ordine r=-1. Si distingue in

media armonica semplice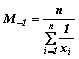

e ponderata 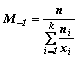(con n_i = frequenze assolute) o 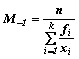(con f_i = frequenze relative)

Proprietà della media armonica

Le proprietà della media armonica si possono ricavare da quelle della media aritmetica tenendo presente che la media armonica altro non è che il reciproco della media aritmetica dei reciproci dei termini della variabile statistica.

- la somma degli scarti dei reciproci dei termini dal reciproco della media armonica è nulla:

- la somma dei quadrati degli scarti dei reciproci dei termini dal reciproco della media armonica è minimo: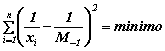  

3.4 MEDIA QUADRATICA

La media quadratica è una media potenziata di ordine r=2. Si distingue in

media quadratica semplice   

e media quadratica ponderata (con n_i frequenze assolute)

(con f_i frequenze relative)