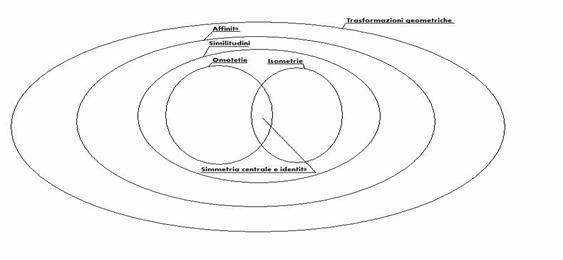
SCHEMA PER LO STUDIO DI TRASFORMAZIONI

matematica

SCHEMA PER LO STUDIO DI TRASFORMAZIONI 

• Calcolo del modulo della trasformazione =

<0 trasformazione inversa

>0 trasformazione diretta

=0 non è una trasformazione

||=k² che è il rapporto di affinità e quindi il rapporto tra le aree di figure corrispondenti

Se =1 l'affinità si dice equivalente perché conserva le aree di figure corrispondenti.

• Si controlla se l'affinità è una similitudine guardando se muta circonferenze in circonferenze.

Si considera l'equazione X²+Y²=r² e si guarda se la trasformata è ancora una circonferenza. Si dimostra che per una similitudine si ha

Una particolare similitudine è l'omotetia che ha equazioni  in cui |k| è il rapporto di omotetia. Se |k|>1 si ha un ingrandimento, se |k|<1 si ha un rimpicciolimento.

L'omotetia ha un punto unito che è il centro di omotetia e un fascio proprio di rette unite avente centro nel centro di omotetia.

Se una similitudine ha ||=1, allora è una isometria. La classificazione avviene in base agli elementi uniti.

• Ricerca degli elementi uniti

Gli elementi uniti sono soluzione del sistema  e cioè .

Tale sistema è di primo grado e quindi può ammettere

0 soluzioni--------- nessun elemento unito

1 soluzione-------- 1 punto unito

Infinite soluzioni------ una retta luogo di punti uniti

Si devono poi ricercare le rette unite del tipo Y=mX+q e X=t applicando la trasformazione

NB: quando hai una curva del tipo y=f(x) e devi trovarne la trasformata , spesso sei costretto a determinare la trasformazione inversa. Per determinarla basta risolvere il sistema

 rispetto alle incognite x y.

Classificazione delle isometrie in base agli elementi uniti