TEOREMI E DIMOSTRAZIONI - TEOREMA (DELL'UNICITÀ DELL'ESTREMO SUPERIORE E INFERIORE)

TEOREMA (DEL QUOZIENTE TRA POLINOMI)

Siano M e N due polinomi con grado(M) ≥ grado(N). Allora esistono due polinomi Q e R con grado(R) < grado(N) tali che:

M = Q * N + R

(M= dividendo, Q= quoziente, N= divisore, R= resto)

TEOREMA (REGOLA DI RUFFINI)

Sia M un polinomio; allora c è radice di M se e solo se M è divisibile per N=(x-c), cioè se esiste un polinomio Q tale che:

M=Q(x)(x-c)

DIMOSTRAZIONE

Ipotesi: c è radice di M → M(c)=0

Tesi: M(x) = Q(x) (x-c)

Poiché M e N si possono dividere, allora esistono Q e R tali che M = Q(x) * N = (x-c)+R(x)

grado(R)<grado(N) = grado(x-c) = 1

grado R=0 cioè R(x) = (costante)

Dunque posso riscrivere che M(x) = Q(x) * (x-c) +

Uso l'ipotesi: M(c) = Q(c) * (c-c) + = = 0

M(c) è la costante ma per ipotesi M(c) deve essere uguale a 0 quindi =0 cioè R(x) = 0 e quindi vale la tesi M(x) = Q(x) (x-c)

VICEVERSA

Ipotesi: M(x) = Q(x) (x-c)

Tesi: c è radice di M → M(c)=0

Calcolo M(c): M(c) = Q(c) * (c-c) = Q(c) * 0 = 0.

Quindi la tesi è verificata (c è radice di M)

TEOREMA (SUI LIMITI)

Se e , allora risulta che:

1)            (limite della somma = somma dei limiti);

2)            (limite del prodotto = prodotto dei limiti);

3) se 0               (limite del quoziente = quoziente dei limiti).

TEOREMA (DI UNICITÀ DEL LIMITE)

Se la funzione f ammette limite, per x→, questo limite è unico.

DIMOSTRAZIONE PER ASSURDO

Neghiamo la tesi e mostriamo che questo genera un assurdo.

Ipotesi: Esiste

Tesi: ℓ è unico.

Supponiamo che esistano due limiti  (a) e (b) e supponiamo che .

(a) significa tale che ;

(b) significa tale che .

Nell'intersezione dei due intorni ():

→ < f(x) < → < → →

( poiché per ipotesi, risulta che la quantità è positiva; questo è un ASSURDO perché per definizione di limite, ε deve essere un qualunque numero > 0 e piccolo a piacere, quindi anche un numero < di .

TEOREMA DEL CONFRONTO SUI LIMITI

Siano f(x) e g(x) due funzioni definite in uno stesso e siano e .

1) Se , allora esiste un intorno (diverso da ) tale che risulta:

f(x) > g(x) quando .

2) Se f(x) ≤ g(x) , allora .

3) TEOREMA DEI CARABINIERI:

Sia h(x) una funzione definita su e tale che f(x) < h(x) < g(x).

Se () cioè se =, ne segue che

TEOREMA (OPERAZIONI TRA FUNZIONI CONTINUE)

Siano f(x) e g(x) due funzioni continue su un insieme A. Allora risulta che:

la somma (f(x)+g(x)) è continua in A;

il prodotto f(x)*g(x) è continuo in A;

il rapporto , se esiste, è continuo in A;

la composizione , se esiste, è continua in A.

TEOREMA DI WEIERSTRASS

Sia f continua in . Allora risulta:

f è limitata cioè il dominio di f è limitato;

f ha massimo (M) e minimo (m), cioè esistono in punti di massimo e di minimo assoluto;

f assume tutti i valori compresi tra il suo minimo (m) e il suo massimo (M), cioè

  Cod f = .

TEOREMA DEGLI ZERI

Sia f continua in e sia f(a)*f(b)<0. Allora esiste un punto c tale che f(c)=0.

TEOREMA (LEGAME TRA CONTINUITÀ E DERIVABILITÀ)

Se f è derivabile in , allora f è continua in , cioè la continuità in è condizione necessaria per la derivabilità in .

DIMOSTRAZIONE

Tesi: f è continua cioè .

Ipotesi: f è derivabile cioè (finito→devo supporre che il limite sia finito perché altrimenti verrebbe una forma indeterminata)

Scrivo f(x) nella forma:

f(x) =

Posso allora scrivere :

=

==

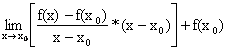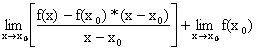* 0 + = ( è un numero, quindi il limite è il numero stesso)

→ LA TESI È DIMOSTRATA

TEOREMA DELLA DERIVATA NULLA ( O DI FERMAT)

Sia f definita in A. Se risulta:

f è derivabile in

è interno ad A

è punto di max o di min relativo

Allora .

DIMOSTRAZIONE

Supponiamo punto di minimo relativo, quindi esiste un tale che →.

Poiché è interno ad A, distinguo i punti che si trovano a destra e sinistra di per studiare il segno del rapporto incrementale.

Considero     (i punti a sinistra di )

dunque per è ≤0

Considero    (i punti a destra di )

dunque per è ≥0

Dunque per il TEOREMA DEL CONFRONTO SUI LIMITI risulta che:

Poiché f deve essere derivabile in , allora deve risultare , ma questo è possibile solo se = 0  cioè se == 0.

CONSEGUENZE DEL TEOREMA DELLA DERIVATA NULLA

TEOREMA DI ROLLE (TEOREMA DELL'ESISTENZA DEI PUNTI STAZIONARI)

Sia f continua e derivabile in un intervallo chiuso e limitato e sia . Allora esiste un punto tale che .

Il teorema afferma l'esistenza di un punto stazionario, cioè un punto con derivata prima uguale a zero.

Osservazioni:

1) Per il TEOREMA DI WEIERSTRASS, f ha massimo (M) e minimo (m).

2) Poiché , allora f è costante (M=m) e quindi ci sono infiniti punti a derivata prima uguale a zero. Se invece m<M allora uno dei due cade all'interno di perché sul bordo la funzione assume valori uguali e quindi ho trovato un punto di massimo o di minimo relativo dove f è derivabile, interno ad dunque per il TEOREMA DELLA DERIVATA NULLA, la derivata prima è zero.

TEOREMA DI LAGRANGE

Sia f continua in e derivabile in (a,b). Allora esiste un punto tale che ↓

è il coeff. angol. della retta
che unisce (a,f(a)) e b(, f(b))

Il teorema di Lagrange afferma che esiste un punto c dove la retta tangente al grafico è parallela alla retta secante il grafico nei punti (a,f(a)) e b(, f(b)).

CONSEGUENZE DEL TEOREMA DI LAGRANGE

TEOREMA DI L'HÔPITAL

Siano f(x) e g(x) due infinitesimi o due infiniti per e siano due funzioni derivabili in un intorno di . Allora, se esiste , tale limite è uguale al .

Cioè: =

TEOREMA DEL LIMITE DELLA DERIVATA

Sia f continua in e sia f derivabile in un intorno del punto escluso .

Allora se esiste finito , f è derivabile in e la derivata .

DIMOSTRAZIONE

f è derivabile in se esiste finito

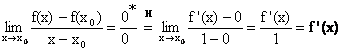
Poiché f è continua in ,

TEOREMA

Sia f continua in . Allora risulta che:

• se f è crescente fino a e poi decrescente, è PUNTO DI MAX RELATIVO;
• se f è decrescente fino a e poi crescente, è PUNTO DI MIN RELATIVO.

TEOREMA DEL SEGNO DELLA DERIVATA

Sia f derivabile in (a,b).

a)  Se allora f è STRETTAMENTE CRESCENTE in (a,b) → è invertibile;

b)  Se allora f è STRETTAMENTE DECRESCENTE in (a,b) → è invertibile;

c)  Se allora f è COSTANTE in (a,b).

N.B.: In realtà il teorema vale anche in forma più debole, cioè:

a) Se e zero solo in un numero finito di punti allora f è STRETTAMENTE CRESCENTE in (a,b);

b) Se e zero solo in un numero finito di punti allora f è STRETTAMENTE DECRESCENTE in (a,b).

DIMOSTRAZIONE

Ipotesi:

Tesi: f strettamente crescente in (a,b) cioè . Applico il TEOREMA DI LAGRANGE ad f nell'intervallo [x₁,x₂]. Posso applicare il teorema in [x₁,x₂] perché l'intervallo [x₁,x₂] quindi f è derivabile in tutto [x₁,x₂] e quindi anche continua.

Dal teorema di Lagrange risulta:

  ↓ ↓
>0 per ipotesi    >0

Quindi =→>0 quindi anche l'altro membro è >0 dunque LA TESI È DIMOSTRATA ↓ ↓
>0 >0

TEOREMA (FUNZ. CONVESSA →MINIMO ASSOLUTO)

Sia f derivabile in (a,b) e convessa. Allora, se è un punto stazionario (), è PUNTO DI MINIMO ASSOLUTO (in (a,b)).

DIMOSTRAZIONE

Tesi: è punto di minimo assoluto cioè

Ipotesi: f è convessa in (a,b)

Poiché f è derivabile e convessa in (a,b) allora risulta che .

Poiché per ipotesi, sostituendo 0 a si ottiene . Quindi , dunque è PUNTO DI MINIMO ASSOLUTO → LA TESI È DIMOSTRATA.

TEOREMA (FUNZ. CONCAVA →MASSIMO ASSOLUTO)

Sia f derivabile in (a,b) e concava. Allora, se è un punto stazionario (), è PUNTO DI MASSIMO ASSOLUTO (in (a,b)).

DIMOSTRAZIONE

Tesi: è punto di massimo assoluto cioè

Ipotesi: f è concava in (a,b)

Poiché f è derivabile e concava in (a,b) allora risulta che .

Poiché per ipotesi, sostituendo 0 a si ottiene . Quindi , dunque è PUNTO DI MASSIMO ASSOLUTO → LA TESI È DIMOSTRATA.

TEOREMA (FUNZIONE CONVESSA, CONCAVA, LINEARE)

Sia f derivabile due volte in (a, b).

• Se → f è CONVESSA in (a, b);
• Se → f è CONCAVA in (a, b);
• Se → f è LINEARE in (a, b).

TEOREMA (PUNTO DI FLESSO)

Sia f derivabile due volte in e continua in .

a)  Se è PUNTO DI FLESSO allora .

b)  Se e (o ) in un intorno sinistro e (o ), allora è un PUNTO DI FLESSO.