|
|
| |
![]() - Situazioni economiche e principio di
- Situazioni economiche e principio di
![]() equivalenza finanziaria.
equivalenza finanziaria.
![]() - Valutazioni di rendite.
- Valutazioni di rendite.
![]() - Ammortamenti.
- Ammortamenti.
![]() PREREQUISITI
PREREQUISITI
![]()
![]() SAPERE
SAPERE
![]()
![]() - quando
due grandezze sono direttamente proporzionali;
- quando
due grandezze sono direttamente proporzionali;
![]() - proprietà
delle potenze;
- proprietà
delle potenze;
![]() - definizione
di logaritmo e sue proprietà;
- definizione
di logaritmo e sue proprietà;
![]() - funzione
lineare, funzione esponenziale, funzione logaritmica;
- funzione
lineare, funzione esponenziale, funzione logaritmica;
![]() - somma
dei primi n termini di una progressione
geometrica.
- somma
dei primi n termini di una progressione
geometrica.
![]()
![]()
![]()
SAPER FARE
![]() - operare
con le percentuali;
- operare
con le percentuali;
![]() - risolvere
equazioni di primo e secondo grado;
- risolvere
equazioni di primo e secondo grado;
![]() - risolvere
equazioni esponenziali con i logaritmi;
- risolvere
equazioni esponenziali con i logaritmi;
![]() - leggere
un grafico su un piano cartesiano;
- leggere
un grafico su un piano cartesiano;
![]() - disegnare
il grafico di semplici funzioni;
- disegnare
il grafico di semplici funzioni;
- operare per interpolazione lineare ORARIO CORSO IGEA E CORSO MERCURIO
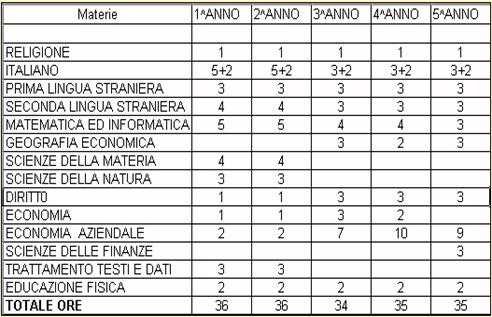 CORSO
IGEA
CORSO
IGEA
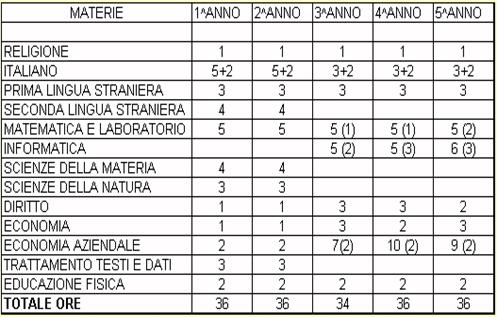
CORSO MERCURIO
La politica
finanziaria La politica
del bilancio Il bilancio
dello Stato SCIENZE DELLE FINANZE


DIRITTO
ECONOMIA
APPUNTI
OPERAZIONE FINANZIARIA DI CAPITALIZZAZIONE
TERMINI E SIMBOLI
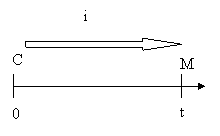 i tasso d'interesse unitario
i tasso d'interesse unitario
t durata dell'investimento
C capitale investito
M montante
I interesse maturato
M = C + I
REGIME FINANZIARIO DELL'INTERESSE SEMPLICE
L'interesse maturato è direttamente proporzionale al capitale impiegato, alla durata e al tasso d'interesse unitario
I = Cit
Legge di capitalizzazione semplice:
M = C(1 + it)
Il regime di cap. semplice viene generalmente applicato per periodi inferiori all'anno.
REGIME FINANZIARIO DELL'INTERESSE COMPOSTO
Gli interessi maturati alla fine di ogni periodo sono capitalizzati per il periodo successivo.
Legge di capitalizzazione composta:
M = C(1 + i)t
(GRAF1)
Una legge di capitalizzazione è scindibile se per trasferire un capitale nel tempo è indifferente che ciò avvenga in una sola volta o con due o più spostamenti successivi.
La legge di capitalizzazione composta è scindibile, quella semplice no.
Due tassi, relativi a due diversi periodi di capitalizzazione, sono equivalenti, quando conducono, a parità di capitale e di tempo, ad uguali montanti.
Se indichiamo con i il tasso annuo e con ik il tasso relativo a un periodo di 1/k di anno, in regime composto, l'equivalenza tra i e ik è data dall'equazione:
1 + i = (1 + ik)k
OPERAZIONE FINANZIARIA DI SCONTO
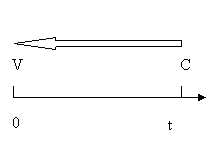 TERMINI E SIMBOLI
TERMINI E SIMBOLI
V valore attuale del capitale C
o somma scontata
C capitale o valore nominale
S sconto è il compenso che spetta
a colui che rende anticipatamente
il capitale C
V = C- S
SCONTO COMMERCIALE
Lo sconto commerciale SC è proporzionale al valore nominale, al tasso di sconto d e al tempo di anticipo t.
SC = Cdt
SCONTO RAZIONALE
Lo sconto razionale è l'interesse semplice, a un dato tasso i, calcolato sulla somma scontata V.
SR = Vit
V = C(1 + it)-1
SCONTO COMPOSTO
Lo sconto composto è calcolato come interesse composto, a un dato tasso i, sulla somma scontata V.
V = C(1 + i)-t
L'operazione di sconto si effettua in questi casi:
PRINCIPIO DI EQUIVALENZA FINANZIARIA
In un regime, due somme, disponibili in tempi diversi, si dicono equivalenti in un dato tasso, se i loro valori al tempo t, sono uguali.
In altre parole possiamo affermare che un'operazione finanziaria è equa se l'insieme delle prestazioni, valutate ad un tempo t, uguaglia l'insieme delle controprestazioni, valutate anch'esse al tempo t.
Poiché la legge composta è scindibile, non ha importanza l'epoca che scegliamo per il confronto: se due capitali hanno lo stesso valore ad una certa epoca, lo hanno ad un'epoca qualunque.
Due capitali che sono equivalenti ad un certo tasso, non sono equivalenti ad un tasso diverso.
RENDITA
Si dice rendita una successione di somme esigibili o pagabili in epoche diverse.
In genere si studiano rendite periodiche a rata costante e si classificano in base al periodo, alla scadenza delle rate, alla durata o alla decorrenza.
Rispetto al periodo una rendita può essere:
-annua -frazionata -poliennale.
Rispetto alla scadenza delle rate può essere:
-anticipata (pagamento all'inizio di ogni periodo)
-posticipata (pagamento alla fine di ogni periodo).
Rispetto alla durata la rendita è detta:
-temporanea -perpetua.
Rispetto alla decorrenza:
-immediata (l'inizio coincide con il momento in cui si stipula il contratto)
-differita (l'inizio è più tardi).
Montante di una rendita immediata posticipata
Tale montante è la somma dei montanti di ciascuna rata calcolati alla fine dell'ultimo periodo.
M = R![]()
M montante; R rata; i tasso; n rate.
Il calcolo del montante di una rendita si usa nei problemi di costituzione di un capitale.
Valore attuale di una rendita immediata posticipata
Il valore attuale di una rendita è il suo valore nel momento in cui è stipulato il contratto con cui si costituisce la rendita. E' la somma dei valori attuali delle singole rate che la compongono.
Resta inteso che la valutazione, però, può essere effettuata in qualsiasi istante.
V = R![]()
Il calcolo del valore attuale di una rendita si usa nei problemi di rimborso di un prestito.
RIMBORSO DI UN PRESTITO
AMMORTAMENTO
Per il rimborso di un debito D si possono seguire, in generale, tre vie:
il debitore pagherà in una sola volta a una data scadenza il capitale più l'interesse, cioè il montante (rimborso globale);
il debitore pagherà periodicamente gli interessi sul debito e, alla scadenza convenuta, in una sola volta l'intero capitale (rimborso globale con pagamento periodico degli interessi);
il debitore pagherà periodicamente gli interessi e anche una parte del capitale, in modo da estinguere a poco a poco il debito (rimborso graduale).
Del terzo tipo si distinguono due diverse forme:
ammortamento a quote costanti di capitale (uniforme);
ammortamento a rata costante (progressivo).
Ammortamento uniforme
Simboli: Qk indica la quota di capitale costituente la k-esima rata;
Rk indica l'importo della k-esima rata;
Ik indica l'interesse da pagare con la k-esima rata;
Dk indica il debito residuo dopo aver pagato la k-esima rata;
Ek indica il debito estinto dopo aver pagato la k-esima rata.
D indica il debito iniziale.
Qk = D/n Ek = kQk Dk = D - Ek Ik = iDk-1 R = Qk + Ik
Ammortamento progressivo
![]() D = R
D = R![]() R =
R = ![]()
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026