·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

Tabella 1.2    Integrali immediati di alcune funzioni elementari

·& 656j91g nbsp;   da cui

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;      da cui

·& 656j91g nbsp;   da cui
e

·& 656j91g nbsp;   da cui

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

Tabella 1.3    Integrazione per sostituzione

 

Tabella 1.4    Integrazione per parti

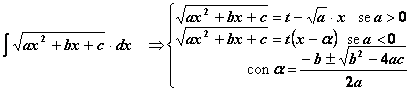
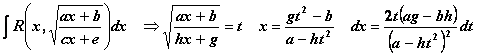
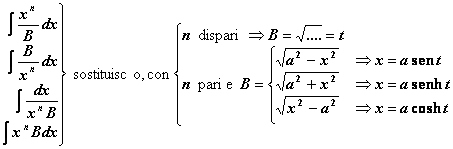
Tabella 1.5    Integrazione di funzioni razionali fratte

1.& 656j91g nbsp; se ammette radici reali distinte (di molteplicità 1) si ottiene:

2.& 656j91g nbsp; se ammette radici reali rispettivamente di molteplicità

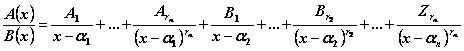
3.& 656j91g nbsp; se ammette radici reali di molteplicità e radici complesse coniugate:

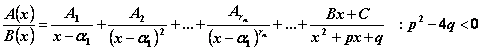
In questi casi si ottengono integrali del tipo facilmente determinabili, e altri del tipo riconducibili (attraverso completamenti di quadrati e procedimenti di somma/sottrazione al numeratore) ad integrali del tipo

4.& 656j91g nbsp; se le radici complesse coniugate hanno molteplicità diversa da 1, si applica la formula di Hermite: date di molteplicità , e una coppia di radici complesse di molteplicità (con polinomio di grado inferiore di una unità rispetto al denominatore):

Tabella 2.1    Sviluppi di Mc Laurin per alcune funzioni elementari

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

·& 656j91g nbsp;  

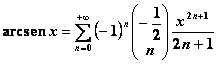
·& 656j91g nbsp;  

·& 656j91g nbsp;   con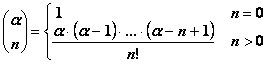

convergente per e per se

Tabella 2.2    Serie notevoli

·& 656j91g nbsp;   progressione aritmetica:

·& 656j91g nbsp;   progressione geometrica:

per

·& 656j91g nbsp;   binomio di Newton:    

Tabella 3.1: Funzioni trigonometriche

·& 656j91g nbsp;   Relazioni generali

sec

·& 656j91g nbsp;   Somma e sottrazione

  

·& 656j91g nbsp;   Duplicazione

   

·& 656j91g nbsp;   Bisezione

 

·& 656j91g nbsp;   Parametriche

·& 656j91g nbsp;   Werner

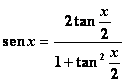
Tabella 3.2: Funzioni iperboliche

·& 656j91g nbsp;   Relazioni generali

  

   con

    con

con

·& 656j91g nbsp;   Somma e sottrazione

·& 656j91g nbsp;   Duplicazione

·& 656j91g nbsp;   Bisezione

   

  

·& 656j91g nbsp;   Parametriche

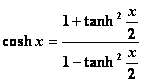
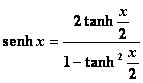
·& 656j91g nbsp;   Werner