NUMERI COMPLESSI

Numeri Immaginari

Non esiste alcun numero reale il cui quadrato sia 545e41f –1; creiamo allora un numero, al di fuori dell’insieme dei reali, che abbia tale caratteristica, e chiamiamolo i : unità immaginaria.

Si ha, per definizione:

i

Dato che si conservano le proprietà algebriche, si ha anche di conseguenza:

(-i)

Esistono due numeri, nell’insieme I dei numeri immaginari, il cui quadrato fa –1: i e –i .

Come per i numeri reali, vale che

i · 1 = i i ·

Se b è un numero reale, il prodotto bi si chiama numero immaginario.

bi = ib

I numeri bi e –bi si dicono numeri immaginari opposti.

Per le potenze ad esponente intero valgono le consuete proprietà valide per i reali, dunque si ha:

i

i¹ = i ;

i

i³ = i² · i = -1 · i = -i

cioè le prime quattro potenze di i sono: 1, i, -1, -i. Le successive si riproducono indefinitamente nello stesso ordine (i alla 4° sarà i² · i² = -1 · -1 = 1, ecc.). Allo stesso modo:

i²³ = i(4·5)+3 = 1(5) · i³ = i³ = i² · i = -i

Per calcolare iª , dunque, si divide a per 4: resterà

a = 4k + r (dove con k si indica il quoziente, con r il resto).

Si avrà:

iª = 1(k) ּ i(r) = 1 ּ i(r ) = i(r) dove r = 0,1,2,3

Risulta che l’addizione e la sottrazione di numeri immaginari dà come risultato un numero immaginario, mentre il prodotto e il quoziente di due numeri immaginari è un numero reale.

8i + 6i = 14i;

21i – 7i = 14i;

4i ּ (-2i) = -8i² = -8 · -1 = 8

-√2i • ½i = √2/2 i² = -√2/2

Il quadrato di un numero immaginario è sempre un numero reale negativo.

Numeri Complessi

Un numero complesso è un numero del tipo:

a + bi

dove a è la parte reale,

b è il coefficiente immaginario.

L’insieme di tali numeri costituisce il campo dei numeri complessi.

Se b, cioè il coefficiente immaginario, è nullo (b=0), il numero complesso a +bi si riduce al numero reale a;

se è a=0, il numero a +bi coincide con il numero immaginario bi.

Gli insiemi R dei numeri reali e I dei numeri immaginari, dunque, sono entrambi sottoinsiemi di C, insieme dei numeri complessi.

Due numeri complessi sono uguali quando hanno uguali le parti reali e i coefficienti immaginari:

a + bi = c + di se e solo se a = c , b = d

Se due numeri complessi non sono uguali, si dicono disuguali, ma non si può stabilire quale tra loro sia più grande o più piccolo, quale maggiore e quale minore, perché nei complessi non si ha la relazione di ordinamento che invece è presente sulla retta reale.

Un numero complesso è uguale a zero se ha nulli sia la parte reale sia il coefficiente immaginario:

a + bi = 0 se e solo se a = 0, b = 0

Bisogna ora distinguere tra due concetti: quello di coniugato e quello di opposto:

Due numeri complessi che hanno la stessa parte reale e opposti coefficienti immaginari, si dicono complessi coniugati

Sono coniugati, ad esempio: 8 + 3i e 8 – 3i

14 + ¾ i e 14 - ¾ i

Due numeri complessi si dicono opposti quando sono numeri opposti tra loro sia le parti reali, sia i coefficienti immaginari.

Sono opposti, ad esempio: 2 + 5i e -2 – 5i

√2 - 0.2 i e -√2 + 0.2 i

La somma di due numeri complessi si esegue sommando le due parti reali e sommando i due coefficienti immaginari.

(2 + 3i) + (5 – 7i) = (2+5) + (3-7)i = 7 – 4i

La differenza di due numeri complessi è semplicemente la somma del primo con l’opposto del secondo.

Si ha: (a + bi) - (a – bi) = 2bi , cioè la differenza di due numeri complessi coniugati è un numero immaginario.

Il prodotto di due numeri complessi è dato dall’uguaglianza:

(a +bi)(c +di) = (ac – bd) + (bc + ad)i

Infatti, se svolgiamo:

(a + bi)(c + di) = ac + adi + bci + bdi² = ac + i(ad + bc) – bd = (ac – bd) + (bc + ad)i

In particolare si ha: (a + bi)(a – bi) = a² + b² , cioè il prodotto di un numero complesso per il suo coniugato è un numero reale positivo, ed è uguale al quadrato della parte reale + il quadrato del coefficiente immaginario.

Se l’ultima relazione la leggiamo al rovescio, otteniamo che nell’insieme dei numeri complessi la somma di due quadrati è decomponibile nel prodotto di due numeri complessi coniugati:

a² + b² = (a + bi)(a – bi) oppure: a² + b² = (b + ai)(b – ai)

Es: 9x² + 4y² = (3x + 2yi)(3x – 2yi) = (2y + 3xi)(2y – 3xi)

2 + 9 = (√2 + 9i)(√2 – 9i) = (9 + √2 i)(9 - √2 i)

Il reciproco di a + bi (diverso da zero) si indica con 1 ed è definito come quel numero

a +bi

che, moltiplicato per a + bi, dà 1.

Proviamo a moltiplicare sopra e sotto per il suo coniugato:

1 a - bi a - bi

= =

a + bi (a + bi)(a – bi) a² + b²

a - bi

Dunque il reciproco di a + bi è

a² + b²

Per quoziente di due numeri complessi si intende il prodotto del primo per il reciproco del secondo.

1 3 + i 3 + i

Es: (2 + 5i) : (3 – i) = (2 + 5i) · = (2 + 5i) · = (2 + 5i) · =

3 – i 9 - i² 9 + 1

(2 + 5i) (3 + i) (6 – 5) + (15 + 2)i 1 + 17 i 1 17

= = = + · i

10 10 10 10 10

Definite così le proprietà formali delle operazioni fondamentali, si può operare con in complessi allo stesso modo che con i reali, avendo l’accortezza di sostituire –1 ad i² .

Così, per l’elevamento a potenza si applicano le regole consuete, tenendo presente, come abbiamo già detto, che i² = -1, e che le prime quattro potenze di i sono 1, i, -1, -i, e così si ripetono all’infinito.

Es: (√2 – 5i)² = (si sviluppa il quadrato del binomio): 2 + 25i² -2·5·√2i = -23 -10·√2i

Risoluzione di equazioni di secondo grado nell’insieme dei numeri complessi

Operando con i numeri reali, le soluzioni di un’equazione algebrica di secondo grado si possono trovare solo se il suo determinante (o discriminante) è positivo o nullo, mentre niente se ne può dire se è negativo. I numeri complessi, e in particolare i numeri complessi coniugati, rappresentano le soluzioni di tali equazioni a determinante negativo.

Data l’equazione nella forma ax² + bx + c = 0

il determinante risulta essere ∆ = b² - 4ac

Le soluzioni si calcolano con la formula:

-b ± √∆

X =

2a

Se ∆ > 0 si hanno due soluzioni reali

Se ∆ = 0 si ha una sola soluzione reale

Se ∆ < 0 non ci sono soluzioni reali; infatti si dovrebbe fare l’operazione di estrazione di radice di un numero negativo, e questo nei reali è impossibile.

Ma adesso che lavoriamo nei complessi, l’operazione è lecita, quindi esistono soluzioni anche se ∆ < 0.

Infatti, se ∆ < 0, allora - ∆ > 0, quindi:

√∆ = √ - (- ∆) = √ -1 • √ -∆ = ± i • √ -∆

e qui √-∆ è un numero reale, perché -∆ > 0.

La formula, dunque, esprime due numeri complessi coniugati dati da:

-b ± i · √-∆

X =

2a

Es Risolvere l’equazione x² -7x +25 = 0, con x € C

∆ = (-7)² - (4 · 1 · 25) = -51 , quindi non ci sono soluzioni reali. Applichiamo la formula:

7 ± √-51 7 ± i · √51

x = x = e troviamo così due numeri complessi coniugati .

Rappresentazione geometrica dei numeri complessi

Esiste una corrispondenza biunivoca tra le coppie di numeri reali e i punti di un piano: basti pensare al piano cartesiano, dove ad ogni punto è associata una coppia di numeri e viceversa. Dato che i numeri complessi sono a tutti gli effetti composti da una coppia di numeri reali (parte reale e coefficiente immaginario) possiamo dunque pensare di rappresentarli come punti di un piano cartesiano.

Y Fissiamo quindi sul piano un sistema di assi cartesiani di origine

O. Il numero complesso a + bi è caratterizzato dalla coppia di

numeri reali a e b. Il punto P, di ascissa “a” e di ordinata “b”,

a P è la rappresentazione geometrica del numero complesso a + bi.

b

o x

Quando b = 0, il numero complesso si riduce ad un semplice numero reale (infatti b, il coefficiente immaginario, è zero) , e in effetti il punto P giace sull’asse x, che corrisponde quindi alla retta reale. L’asse x si dice asse reale

Quando a = 0, è la parte reale ad annullarsi, e si ha un numero immaginario. Il punto P giace sull’asse y, che risulta quindi l’asse immaginario.

L’origine O è l’immagine dello zero complesso: a = 0, b = 0.

Il piano considerato come luogo dei punti che sono immagini geometriche dei numeri complessi, si dice piano di Gauss.

Nel piano di Gauss, due numeri complessi coniugati hanno per rispettive immagini due punti simmetrici rispetto all’asse reale x;

due numeri complessi opposti sono invece rappresentati da punti simmetrici rispetto all’origine O degli assi.

2 + i

2 - i (coniugato di 2 + i)

-4 -3 -2 -1 1 2 3 4

-3 + 4i

3 – 4i (opposto di –3 + 4i)

3i (numero immaginario)

Corrispondenza tra vettori e numeri complessi

P (a ; b)

v 

0

Consideriamo il numero complesso a + bi e la sua rappresentazione sul piano di Gauss, cioè il punto P.

Prendiamo poi il vettore v che abbia la “coda” nell’origine O e la “punta” nel punto P.

Si ha che i numeri a e b, parte reale e coefficiente immaginario del numero, risultano le componenti cartesiane del vettore v: a è la componente lungo l’asse delle ascisse, b quella lungo l’asse delle ordinate.

Diremo allora che il vettore v è associato al numero complesso a + bi e viceversa.

Esiste quindi una corrispondenza biunivoca tra i numeri complessi e i vettori del piano: ad ogni numero complesso è associato un vettore, e ad ogni vettore è associato un numero complesso.

Consideriamo i due numeri complessi = a + bi e = c + di.

Ad essi sono associati i due vettori v1=OP e v2=OQ , dove P è il punto di ascissa a e ordinata b: P(a;b), e Q è il punto di ascissa c e ordinata d: Q(c;d).

v1 quindi rappresenta

v2 rappresenta

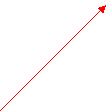
R(a+c ; b+d)

Q(c;d)

V1+v2

V2

P(a;b)

V1

Sommiamo v1 e v2 con la regola del parallelogrammo: la diagonale OR risulta il vettore somma: v = v1+v2.

Si può dimostrare che a tale vettore corrisponde un particolare numero complesso, cioè la somma dei due numeri φ e ω. ( v rappresenta )

La somma dei vettori associati a due numeri complessi è il vettore associato alla somma dei numeri complessi considerati.

Modulo e argomento di un numero complesso

Consideriamo il numero complesso a + bi, rappresentato sul piano di Gauss dal vettore OP, dove P è il punto di ascissa a e ordinata b.

La lunghezza di OP(cioè la distanza del punto P dall’origine O) si può calcolare facilmente, essendo note le sue coordinate a e b:

d(P,O) = √ a² + b²

Tale numero si dice modulo del numero complesso a + bi ,e si indica ponendo il numero complesso tra due sbarre verticali.

| a + bi | = √a² + b²

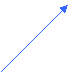
P

|a+bi|

Il vettore OP, inoltre, forma un angolo Φ con il semiasse b

delle ascisse: quest’ angolo è detto argomento del   Φ

numero complesso.    O a H

Si conviene che Φ sia un angolo positivo o nullo minore di un angolo giro:

0 ≤ Φ < 360°

Consideriamo ora il triangolo rettangolo POH: si ha che l’angolo Φ è tale che:

HP

tg = . Ma P è l’immagine del numero complesso a+bi, e sappiamo che

OH HP=b e OH=a; quindi si ha:

b

tg =

a

Si ha che:

Lo zero complesso ha modulo nullo, poiché ha come immagine il punto O, origine del piano di Gauss.

Il modulo di ogni numero complesso, escluso lo zero, è un numero reale positivo.

Quando il numero complesso è un numero reale, il suo modulo coincide con il valore assoluto del numero reale (infatti le immagini dei numeri reali nel piano di Gauss sono punti dell’asse x).

L’argomento di un numero reale positivo è l’angolo nullo, mentre l’argomento di un numero reale negativo è l’angolo piatto.

Il modulo di un numero immaginario è il valore assoluto del suo coefficiente.

Se il coefficiente di un numero immaginario è positivo, l’argomento di tale numero immaginario è l’angolo retto, mentre se è negativo, l’argomento è tre angoli retti (270°).

L’argomento dello zero complesso è indeterminato (il segmento OP degenera nel punto O).

Due numeri complessi coniugati hanno moduli uguali:

|a + bi| = √a² + b² e |a – bi| = √a² + (-b)² = √a² + b² .

Gli argomenti di due numeri complessi coniugati sono angoli esplementari, Φ e

360° -Φ (infatti le immagini di due numeri complessi coniugati sono punti simmetrici

rispetto all’asse reale x).

Poiché (a + bi)(a – bi) = a² + b² , si può dire che il prodotto di due numeri complessi

coniugati è il numero reale uguale al quadrato del loro modulo.

Θ Forma trigonometrica dei numeri complessi

Sia a + bi un numero complesso, P la sua immagine geometrica, m il suo modulo e θ il suo argomento.

Si ha che:

P

b a = m · cos ; b = m ·sen

a

Allora si può scrivere:

a + bi = m · cos θ + i ·m sen θ

cioè:

a + bi = m · (cos θ+ i · sen θ)

che è la rappresentazione in forma trigonometrica del numero complesso a + bi (a + bi è la forma algebrica).

Per determinare univocamente un numero complesso con la sua forma trigonometrica, occorrono due informazioni: il modulo e l’argomento del numero.

Sappiamo che il modulo di a + bi è:

m = √ a² + b²

Sappiamo poi che a = m cos θ e b = m sen θ, da cui si ricava che

cos θ = a/m e sen θ = b/m;

ma noi sappiamo, grazie alla formula precedente, quant’è il modulo, quindi:

a  b

cos = ; sen

√ a² + b² √ a² + b²

Già con queste formule si può ricavare θ, se questo è un angolo notevole.

Altrimenti si divide la seconda per la prima, ottenendo

b

tg (a = 0)

a

e l’angolo si può trovare eseguendo, con una calcolatrice, arctg b/a.

Se è a > 0 , cioè cos θ > 0,

allora θ è un angolo del 1° o del 4° quadrante, quindi si può assumere θ = arctg b/a.

Se invece è a < 0, cioè cos θ < 0,

allora θ è un angolo del 2° o del 3° quadrante, e si assumerà quindi θ = π + arctg b/a

In particolare:

i numeri reali (b = 0) hanno per argomento 0 o π ( 0 i reali positivi, π i reali negativi);

i numeri immaginari (a = 0) hanno per argomento π/2 o 3π/2 , secondo che il coefficiente dell’unità immaginaria i sia positivo o negativo.

Es. Scrivere in forma trigonometrica il numero - √2 + √2 i

a = - √2 ; b = √2

m = √ a² + b² = √ 2 + 2 = 2

a - √2 b √2

cos = = ; sen = =

m 2 m 2

Si ne deduce immediatamente che è θ = 3π/4.

Si può anche seguire il procedimento completo:

tg = b/a = -1

E’ a < 0, quindi: θ = π + arctg (-1) = π + (- π/4) = 3π/4

Adesso si può scrivere il numero in forma trigonometrica:

- √2 + √2 i = 2 ( cos 3π/4 + i · sen 3π/4).

Prodotto di due numeri complessi in forma trigonometrica:

m1(cosθ1 + i senθ2) · m2(cosθ2 + i senθ2) = m1 m2 [cos (θ1+θ2)+ i sen (θ1 + θ2)]

Quoziente di due numeri complessi in forma trigonometrica:

m1 (cos 1 + i sen 1) m1

= · [cos ( 2) + i sen( 2)]

m2 (cos 2 + i sen 2) m2

Potenza di un numero complesso:

[ m (cosθ + i senθ)]ª = mª ·[cos (aθ) + i sen (aθ)] (formula di De Moivre)

Radici n – esime di numeri complessi:

ª √ m (cos θ + i sen θ) = ª √ m · [ cos ( θ/a + k · 2π/a) + i sen ( θ/a + k · 2π/a)]

con k = 0, 1, 2, . , n-1

Θ Radici n – esime dell’unità

L’equazione

xⁿ = a

con n appartenente ai naturali (escluso lo zero) e a qualsiasi, ha n soluzioni nell’insieme C dei numeri complessi (cosiderando x appartenente a C).

Le soluzioni sono espresse dalla radice ennesima di a ( ⁿ √ a ), che ha quindi, nell’insieme C, n valori distinti.

Se consideriamo il caso particolare a = 1, ci riduciamo a studiare il problema di determinare le radici ennesime dell’unità: esse sono le soluzioni dell’equazione xⁿ = 1, con x elemento di C.

Sappiamo che per n = 2 le soluzioni dell’equazione sono due, +1 e –1 che, in C, si esprimono scrivendo

x = √1

Vediamo quando n = 3, cioè quando l’eq. x³ = 1 è soddisfatta da x = ³√1.

Risolviamo in C:

x³ - 1 = 0

(x – 1) (x² + x + 1) = 0

x – 1 = 0 oppure x² + x + 1 = 0

x1 = 1 ; x2 = -1/2 + i · √3/2 ; x3 = -1/2 – i · √3/2

Rappresentiamo questi tre numeri (le radici terze dell’unità) sul piano di Gauss come A1, A2, A3:

il modulo di ciascun numero è 1, i loro rispettivi argomenti sono

θ1 = 0 , θ2 = 2π/3 , θ3 = 4π/3

A2

I tre punti stanno tutti su una circonferenza di centro

O e raggio 1; i tre punti, inoltre, sono i vertici di un

A1 triangolo equilatero inscritto nella circonferenza di

raggio unitario, con centro nell’origine degli assi e

A3 avente uno dei vertici sul semiasse positivo della x.

In modo del tutto analogo si possono trovare i quattro valori di √ 1 , risolvendo l’equazione

4

X = 1

Questa, infatti, è uguale a:

(x² - 1) (x² + 1) = 0

(x – 1) (x + 1) (x – i ) (x + i) = 0

le soluzioni sono: x1 = 1 ; x2 = -1 ; x3 = i ; x4 = -i

Rappresentiamo questi quattro valori con i quattro punti B1, B2, B3, B4 sul piano di Gauss:

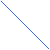
B2

Essi rappresentano i vertici del quadrato (poligono

regolare di 4 lati) inscritto nella circonferenza di

B3 B2 centro O e raggio 1, con uno dei vertici sul

B1 semiasse positivo positivo delle x, e uno sul

semiasse negativo (due soluzioni reali, 4

soluzioni complesse).

Generalizzando, si può affermare che le radici ennesime dell’unità, se è n > 2, sono rappresentate dai vertici del poligono regolare di n lati, avente uno dei vertici sul semiasse positivo delle x e inscritto nella circonferenza di raggio unitario con il centro nell’origine degli assi.

Per rappresentare sul piano di Gauss le n radici ennesime dell’unità, si segna sull’asse x il punto P a distanza 1 dall’origine ( OP = 1); si divide la circonferenza, di centro O e raggio OP , in n parti congruenti a partire da P , determinando sulla circonferenza i punti P , P , . . , Pn-1 che risultano i vertici del poligono regolare P P P Pn-1 di n lati inscritto in tale circonferenza.

6

Ad esempio, se si dovesse risolvere l’equazione X – 1 = 0 (con X appartenente a C), basterebbe calcolare le sei radici seste del numero 1, rappresentate dai vertici di un esagono regolare, inscritto nella circonferenza con centro nell’origine degli assi e raggio unitario (due di questi sei vertici appartengono all’asse x, e sono quindi soluzioni reali dell’equazione).