EQUAZIONI DIFFERENZIALI

y' = dy .

dx

La precedente equazione differenziale, perciò, si può anche scrivere così:

dy . = x ²

dx

INTEGRALE DI UNA EQUAZIONE DIFFERENZIALE-------- ----- ------ -------------

Sia data un'equazione differenziale di ordine n.

Una funzione di equazione y = f (x) si dice soluzione o integrale della prima se, sostituendo la sua espressione e quelle delle sue derivate nell'equazione differenziale data, questa si trasforma in una identità.

Chiamiamo integrale generale la soluzione di un' equazione differenziale del tipo:

y = f (x) + c

rappresentando con c una qualsiasi costante aggiuntiva.

Chiamiamo integrale particolare una funzione la cui equazione si ottiene sostituendo al parametro c, dell'integrale generale, un qualsiasi valore numerico.

ESERCIZIO DI ESEMPIO-------- ----- ------ -------- ----- ------ ----- ----- ---------

y' = x ²    equazione differenziale del primo ordine

dy . = x ² sostituiamo ad y' il rapporto di differenziali

dx

dy = x ² dx utilizziamo le proprietà delle equazioni in modo da poter calcolare l'integrale

∫ dy = ∫ x ² dx applichiamo l'integrale ad entrambi i membri per ottenere la funzione y

y = x ³ + c troviamo così l'integrale generale

3

ESERCIZIO DI ESEMPIO CON CONDIZIONE-------- ----- ------ ----- ----- --------------

Dopo aver trovato l'integrale generale, è possibile che un esercizio ci imponga una condizione per trovare l'integrale particolare.

y' = e ^{-½ x}    equazione differenziale del primo ordine

dy . = e ^{-½ x} sostituiamo ad y' il rapporto di differenziali

dx

dy = e ^{-½ x} dx utilizziamo le proprietà delle equazioni

∫ dy = ∫ e ^{-½ x} dx applichiamo l'integrale ai membri per ottenere la funzione y

y = - 2 ∫ - ½ e ^{-½ x} dx semplifichiamo in modo da poter calcolare l'integrale

y = - 2 e ^{-½ x} + c troviamo l'integrale generale

ponendo la seguente condizione e volendo calcolare c :

y ( 0 ) = 1

y ( x ) = - 2 e ^{-½ x} + c

c = ?

avremo :

1 = - 2 e ⁰ + c

c = ?

da cui ricaveremo il valore c = 3 e quindi avremo l'integrale particolare: y = - 2 e ^{-½ x} + 3

EQUAZIONE DIFFERENZIALE A VARIABILI SEPARABILI-------- ----- ------ ----

Si dice che una equazione differenziale, ad esempio del primo o 535b17f rdine, è a variabili separabili se, ricordando quanto detto sulla rappresentazione di y' come rapporto di differenziali, l'equazione differenziale stessa si può scrivere nella forma:

q ( y ) dy = p ( x ) dx

Con q (y) e p (x) funzioni continue. Questo nuovo concetto ci permette di isolare le variabili.

ESERCIZIO DI ESEMPIO-------- ----- ------ -------- ----- ------ ----- ----- ---------

2xy - y' = 0 equazione differenziale del primo ordine.

2xy - dy . = 0 sostituiamo ad y' il rapporto di differenziali

dx

dy . = 2xy

dx utilizziamo le proprietà delle equazioni

dy = 2xy dx   

A questo punto andiamo ad isolare le variabili, ottenendo dy . = 2x dx

y

dy = ∫ 2x dx applichiamo poi il segno d'integrale ad entrambi i membri

y

log | y | = x ² + c calcoliamo gli integrali riportando un'unica costante c che

assorbe le due costanti c1 e c2 ottenute effettuando le due integrazioni

e ^{log | y |} = e ^{x ² + c} | y | = e ^{x ² + c}

| y | = e ^{x ²} e ^c applichiamo le proprietà delle potenze e per eliminare il modulo della

y modifichiamo l'espressione in questo modo:

y = ± e ^c e ^{x ²} infine sostituiamo a ± e ^c una variabile k

y = k e ^{x ²} otteniamo così l'integrale generale.

EQUAZIONI DIFFERENZIALI LINEARI DI 1° ORDINE-------- ----- ------ -----------

Un'equazione differenziale si dice lineare se è di primo grado rispetto alla funzione incognita y e alle sue derivate, ed è del tipo:

y' = p (x) y + q (x)

con p (x) e q (x) come funzioni continue.

EQUAZIONI OMOGENEE-------- ----- ------ -------- ----- ------ ----- ----- --------

L'equazione differenziale si dice omogenea quando tutti i suoi termini hanno lo stesso grado, come:

y' = p (x) y

Un'equazione di questo tipo è a variabili separabili e quindi si può facilmente risolvere:

y' = p (x) y  equazione differenziale omogenea

dy . = p (x) y sostituiamo ad y' il rapporto di differenziali

dx

dy . = p (x) dx utilizziamo le proprietà delle equazioni e isoliamo le variabili

y

∫ dy . = ∫ p (x) dx applichiamo l'integrale ai membri per ottenere la funzione y

y

log | y | = ∫ p (x) dx + c calcoliamo gli integrali facendo tutti i passaggi

e ^{log | y |} = e ^{∫ p (x) dx + c} | y | = e ^{∫ p (x) dx + c}

| y | = e ^{∫ p (x) dx} e ^c applichiamo le proprietà delle potenze e per eliminare il modulo della

y modifichiamo l'espressione in questo modo:

y = ± e ^c e ^{∫ p (x) dx} infine sostituiamo a ± e ^c una variabile k

y = k e ^{∫ p (x) dx} otteniamo così l'integrale generale.

EQUAZIONI NON OMOGENEE-------- ----- ------ -------- ----- ------ ----------

L'equazione differenziale si dice non omogenea quando non tutti i suoi termini hanno lo stesso grado, come:

y' + p (x) y = q (x)

Per risolvere una equazione di questo tipo applichiamo un metodo detto metodo di Lagrange o metodo della variazione della costante arbitraria.

Esempio:

y' + xy = x  equazione differenziale non omogenea

Si risolve prima di tutto l'equazione omogenea associata all'equazione data, che si ottiene eliminando il termine q (x) che, nell'esempio, è rappresentato dal secondo membro x.

y' + xy = 0  equazione differenziale omogenea associata

dy . = - xy sostituiamo ad y' il rapporto di differenziali

dx

dy . = - x dx utilizziamo le proprietà delle equazioni e isoliamo le variabili

y

∫ dy . = ∫ (- x) dx applichiamo l'integrale ai membri per ottenere la funzione y

y

log | y | = - ½ x ²+ c eseguiamo tutti i passaggi

e ^{log | y |} = e ^{- ½ x ²+ c} | y | = e ^{- ½ x ² + c}

| y | = e ^{- ½ x ²} e ^c applichiamo le proprietà delle potenze e per eliminare il modulo della

y modifichiamo l'espressione in questo modo:

y = ± e ^c e ^{- ½ x ²} infine sostituiamo a ± e ^c una variabile k

y = k e ^{- ½ x ²} otteniamo così l'integrale generale.

A questo punto calcoliamo la derivata dell'integrale generale ottenuto:

y' = k' e ^{- ½ x ²}  + k e ^{- ½ x ²} ( - x)

indicando con k' la derivata di k, non essendo questa una costante.

Infine, sostituiamo le due funzioni trovate y ed y' nell'equazione differenziale non omogenea di partenza :

k' e ^{- ½ x ²}+ k e ^{- ½ x ²} ( - x) + x ( k e ^{- ½ x ²} ) = x

y' y

Eseguiamo le opportune semplificazioni:

k' e ^{- ½ x ²}    - x k e ^{- ½ x ²} + k e ^{- ½ x ²}- x = 0

k' e ^{- ½ x ²} - x = 0 k' = x .

e ^{- ½ x ²}

Passiamo ora a calcolare k' e k come abbiamo sempre fatto con y' e y:

dk . = x . sostituiamo ad k' il rapporto di differenziali

dx e ^{- ½ x ²}

dk = x e ^{½ x ²} dx utilizziamo le proprietà delle equazioni

∫ dk = ∫ x e ^{½ x ²} dx applichiamo l'integrale ai membri per ottenere la funzione k

k = e ^{½ x}+ c otteniamo così la funzione k

La funzione k calcolata va ora sostituita nell'espressione della funzione y = k e ^{- ½ x ²} :

y = (e ^{½ x}+ c ) e ^{- ½ x ²} y = 1 + c e ^{- ½ x ²}

L'espressione ottenuta alla fine è la soluzione dell'equazione differenziale di partenza.

EQUAZIONI DIFFERENZIALI DEL 2° ORDINE-------- ----- ------ ----- ----- ------------

Un'equazione differenziale del secondo ordine è un'equazione in cui compare la variabile indipendente x, una funzione incognita y, la sua derivata prima y' e la sua derivata seconda y" ( tra le derivate può anche comparire solamente y").

Questo tipo di equazioni si risolvono eseguendo una doppia integrazione, come nell'esempio:

y" = 2x equazione differenziale del secondo ordine

dy' . = 2x sostituiamo ad y" il rapporto di differenziali dy'/dx

dx

dy' = 2x dx utilizziamo le proprietà delle equazioni

∫ dy' = ∫ 2x dx eseguiamo la prima integrazione per ottenere la funzione y'

y' = x ² + c otteniamo la funzione y'.A questo punto procediamo per la funzione y

dy . = x ² + c sostituiamo ad y' il rapporto di differenziali dy/dx

dx

dy = (x ² + c ) dx utilizziamo le proprietà delle equazioni

∫ dy = ∫ (x ² + c ) dx eseguiamo la seconda integrazione per ottenere la funzione y

y = x³ . + cx + c1 otteniamo la soluzione finale

3

DISEQUAZIONI IN DUE INCOGNITE-------- ----- ------ -------- ----- ------ --

Le disequazioni in due incognite o in due indeterminate, sono della forma:

F ( x ; y ) ≥ 0

<

Risolverle graficamente significa determinare la parte di piano in cui i punti hanno coordinate che verificano la disequazioni stessa. Questa parte di piano è detta regione delle soluzioni ammissibili.

ESERCIZIO SULLA RISOLUZIONE DELLE DISEQUAZIONI IN DUE INCOGNITE-------

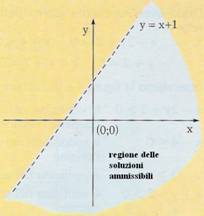
Risolvere la disequazione:    x - y + 1 > 0

Prima di tutto si disegna la retta x - y + 1 = 0 dando dei valori alle variabili x e y :

A questo punto si prende un punto indagine, ad esempio ( 0 , 0 ) e si verifica in quale parte di piano la disequazione è soddisfatta.

Punto indagine: ( 0, 0 )

x - y + 1 > 0 0 - 0 + 1 > 0

L'espressione numerica è vera perciò la disequazione nel punto indagine è soddisfatta e la regione delle soluzioni ammissibili è quella rappresentata in figura.

ESERCIZIO SULLA RISOLUZIONE DI UN SISTEMA DI DISEQUAZIONI----- ----- ---------

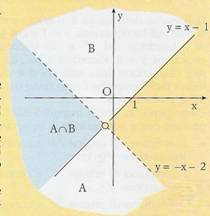
Risolvere il seguente sistema di due disequazioni in due indeterminate:

x + y + 2 < 0

y ≥ x - 1

Si disegnano prima di tutto le due rette x + y + 2 = 0 e y = x - 1 dando dei valori alle variabili x e y.

Si verificano poi quali sono le singole regioni delle soluzioni ammissibili prendendo uno o più punti indagine.

In questo caso prendiamo come unico punto indagine p = ( 0, 0 ) e andiamo a osservare che:

x + y + 2 < 0 0 + 0 + 2 < 0 falso

y ≥ x - 1 0 ≥ 0 - 1 vero

Quindi coloriamo le due parti di piano in cui le disequazioni sono singolarmente soddisfatte. La parte di piano denominata A ∩ B che fa da intersezioni alle due regioni, sarà la regione delle soluzioni ammissibili del sistema.

POLIGONO DELLE SOLUZIONI-------- ----- ------ -------- ----- ------ ---------

Un sistema che ammette soluzioni si dice possibile, altrimenti viene dette impossibile.

Quando un sistema ammette soluzioni rappresentate dai punti di un poligono, si parla di poligono delle soluzioni.

ESERCIZIO SUL POLIGONO DELLE SOLUZIONI-------- ----- ------ ----- ----- --------

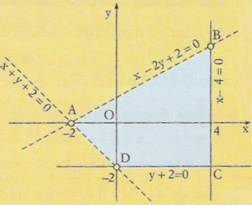
Determinare il poligono delle soluzioni del seguente sistema:

x - 2y + 2 > 0

x - 4 ≤ 0

y + 2 ≥ 0

x + y + 2 > 0

Tracciamo prima di tutto i grafici delle quattro rette:

x - 2y + 2 = 0

x - 4 = 0

y + 2 = 0

x + y + 2 = 0

Dopodichè troviamo le rispettive ragioni di piano delle soluzioni ammissibili, utilizzando un unico punto indagine di coordinate ( 0, 0 ) e otteniamo che:

x - 2y + 2 > 0 0 - 0 + 2 > 0 vero!

x - 4 ≤ 0 0 - 4 ≤ 0 vero!

y + 2 ≥ 0 0 + 2 ≥ 0 vero!

x + y + 2 > 0 0 + 0 + 2 > 0 vero!

Quindi, come intersezioni delle varie parti di piano, avremo l'area rappresentata nella figura.

FUNZIONI DI DUE VARIABILI-------- ----- ------ -------- ----- ------ -----------

Una funzione reale di due variabili reali è una legge che permette di associare a ogni coppia ordinata di numeri reali ( x ; y ) appartenente a un dominio D, uno e un solo numero reale z, del tipo:

z = f ( x ; y )

Il numero reale z si dice immagine della coppia ( x ; y ). Viceversa la coppia ( x ; y ) si dice contro-immagine del valore z.

DOMINIO E CODOMINIO-------- ----- ------ -------- ----- ------ ----- ----- --------

Il dominio D, se non precisato, è l'insieme di tutte le coppie ordinate ( x ; y ) per le quali è possibile determinare il valore di f ( x ; y ) .

Il condominio C, invece, è l'insieme dei valori o insieme di variabilità di f, formato dai valori z che hanno almeno una contro-immagine ( x ; y ) appartenente al dominio D.

RAPPRESENTAZIONE DI UNA FUNZIONE DI DUE VARIABILI----- ----- --------- ----- --------

Il grafico di una funzione reale di una variabile reale è l'insieme reale dei punti del piano cartesiano tra le cui coordinate ( x ; y ) sussiste la relazione y = f (x).

Grafico di una funzione di due variabili:

sia f ( x ; y ) una funzione di due variabili e sia D il suo dominio. A ogni coppia ordinata ( x , y ) appartenente a D possiamo associare il corrispondente valore z = f ( x ; y ) della funzione.

Il grafico, approssimato, si può ottenere in diversi modi:

  disegnando un grafico per punti;

  costruendo i grafici sezione;

  tracciando le curve di livello.

GRAFICI SEZIONE-------- ----- ------ -------- ----- ------ ----- ----- -----------------

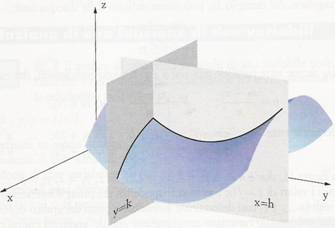
Per rappresentare il grafico di una funzione di due variabili, possiamo separare la sua superficie con piani paralleli ai piani coordinati xz o yz, che vengono detti piani di sezione.

Si determinano così, su questi piani di sezione, delle curve che ne costituiscono l'intersezione con la superficie di equazione z = f ( x ; y ).

Ad esempio, per ottenere un grafico sezione del grafico di

z = f ( x, y )

scegliamo come piano parallelo il piano caratterizzato dall' equazione y = k , con k costante. Poiché tutti i punti di questo piano hanno ordinata k, possiamo dire che:

z = f ( x, k )

Questa equazione a una variabile reale, (dove x è la variabile indipendente e z la dipendente), viene rappresentata graficamente.

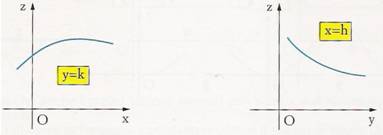
Allo stesso modo si costruisce un grafico di un piano parallelo caratterizzato dall'equazione x = h. La curva ottenuta sarà di equazione:

z = f ( h, y )

Dopo aver disegnato alcuni grafici sezione, ci basterà congiungere le curve ottenute per avere un'idea chiara del grafico di f ( x , y ).

LINEE DI LIVELLO-------- ----- ------ -------- ----- ------ ----- ----- ----------------

Le linee di livello o curve di livello di una funzione, si ottengono sezionandone il grafico con piani paralleli, ciascuno dei quali è il luogo geometrico dei punti dello spazio aventi quota uguale a una costante k e perciò sarà caratterizzato dall'equazione z = k.

Data quindi una funzione di due variabili, una curva di livello è costituita dall'insieme dei punti del grafico di tale funzione aventi tutti la stessa quota .

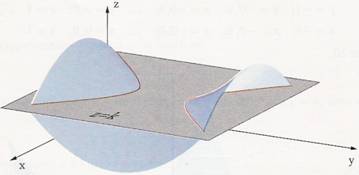
Ad esempio se l'equazione della funzione è

z = f (x, y)

le coordinate dei punti della curva di livello k sono caratterizzate dalle relazioni:

z = k

f ( x , y ) = k

se rappresentiamo graficamente tali linee di livello otteniamo, al variare di k, una serie di curve la cui unione è il dominio della funzione f ( x , y ).

DERIVATE PARZIALI-------- ----- ------ -------- ----- ------ ----- ----- -------------

Con il termine derivate parziali indichiamo le seguenti scritture (1) f ' x e f' y (2).

  La (1) rappresenta la derivata di una funzione unicamente rispetto alla variabile x.

Esempio:

Sia f ( x, y ) = x ³ + y ² - 3x

la sua derivata parziale sarà :

f' x = 3 x ² - 3

in quanto il termine y² verrà considerato come una costante aggiuntiva, e sappiamo che la derivata di una costante ha valore zero.

  La (2) rappresenta la derivata di una funzione unicamente rispetto alla variabile y.

Utilizzando perciò l'esempio di prima:

f ( x, y ) = x ³ + y ² - 3x

la sua derivata parziale sarà :

f' y = 2 y

in quanto i termini x ³ e - 3x verranno considerati come costanti aggiuntive, e sappiamo che la derivata di una costante ha valore zero.

DERIVATE PARZIALI DEL SECONDO ORDINE-------- ----- ------ ----- ----- -----------

Con il termine derivate parziali del secondo ordine indichiamo le seguenti scritture:

(1) f" xx (2) f" yy (3)f" xy (4) f" yx

  La (1) rappresenta la derivata rispetto ad x di una derivata parziale rispetto alla variabile stessa. Si parla praticamente di una doppia derivazione.

Esempio:

Sia f ( x, y ) = y ( x ³ - x )

la sua derivata parziale rispetto alla variabile x sarà :

f' x = 3 x ² y - y

in quanto il termine y² verrà considerato come una costante moltiplicativa, e sfruttiamo le proprietà delle derivate.

A questo punto deriviamo f' x rispetto alla variabile x ed otteniamo:

f" xx = 6xy

utilizzando sempre le proprietà delle derivate.

Questo meccanismo vale anche per f" yy che è la derivata rispetto ad y di una derivata parziale rispetto alla variabile stessa. (2)

  La (3) e la (4) rappresentano, invece, le derivate di derivate parziali ma rispetto alla variabile opposta.

Utilizzando l'esempio di prima:

f ( x, y ) = y ( x ³ - x )

le sua derivate parziali saranno :

f' x = 3 x ² y - y

f' y = x ³ - x

La derivata parziale del secondo ordine f" xy sarà la derivata rispetto ad y della derivata

parziale rispetto alla variabile x, ed avremo:

f" xy = 3 x ² - 1

La derivata parziale del secondo ordine f" yx sarà, invece, la derivata rispetto ad x della derivata parziale rispetto alla variabile y, ed avremo:

f" yx = 3 x ² - 1

Come è facilmente notabile le due derivate di secondo ordine sono uguali.

PUNTI STAZIONARI-------- ----- ------ -------- ----- ------ ----- ----- ---------------

Sia f ( x , y ) una funzione di due variabili definita e parzialmente derivabile in un insieme A.

Se nel punto P ( x_o, y_o ) interno all'insieme A si annullano entrambe le derivate parziali di f, ossia se:

f ' x ( x_o, y_o ) = f ' y ( x_o, y_o ) = 0

diremo che il punto P è un punto stazionario.

Per determinare i punti stazionari di una funzione, occorre calcolarne le derivate parziali e risolvere il sistema di equazioni di incognite x e y che si ottiene per annullare entrambe le derivate parziali:

f ' x ( x_o, y_o )

f ' y ( x_o, y_o )

Le soluzioni di questo sistema, sono le coordinate dei punti stazionari della funzione f.

HESSIANO, PUNTO DI SELLA, PUNTI MINIMO E MASSIMO-------- ----- ------ ---

Per determinare di che tipo è il punto stazionario trovato come soluzione al sistema, si ricorre all' Hessiano.

Si dice Hessiano di una funzione f ( x , y ), dotata di derivate parziali del secondo ordine, la funzione delle due variabili x e y così definita:

H ( x , y ) = f" xx f" xy = f" xx f " yy - f" xy f" yx

f" yx f " yy

Sia f ( x , y ) una funzione di due variabili definita in un insieme A e sia P ( x_o, y_o ) un punto stazionario di f:

  Se H ( x_o, y_o ) > 0 allora :

o   Se f" xx < 0 , Po è un punto massimo;

o   Se f" xx > 0 , Po è un punto minimo.

  Se H ( x_o, y_o ) < 0 allora Po è detto punto di sella

  Se H ( x_o, y_o ) = 0 non si può affermare nulla sulla natura del punto Po.

SERIE NUMERICHE-------- ----- ------ -------- ----- ------ ----- ----- ---------------

Chiamiamo serie numerica o semplicemente serie la somma di infiniti termini di una successione.

Una successione è una funzione particolare che ha come dominio l'insieme dei numeri naturali.

La serie è rappresentabile nel seguente modo:

∑ a_n

ⁿ⁼¹

dove n è l'indice che varia nell'intervallo [ 1, + ∞ ) e a_n è il termine generale.

Per poter lavorare sulle serie, consideriamo un determinato intervallo che chiamiamo serie ridotta di ordine n, che è la somma dei primi n termini della successione, e si indica con S_n.

CARATTERE DELLA SERIE-------- ----- ------ -------- ----- ------ ----- ----- ----

Per determinare il comportamento di una serie andiamo ad analizzare il carattere di essa, cioè andiamo a studiare il limite per n che tende ad infinito della ridotta di ordine n:

lim   S_n = l

ⁿ

Se tale limite è finito diremo che la serie è convergente.

Se il limite è infinito diremo che è divergente.

Se il limite invece non esiste diremo che la serie è o indeterminata o oscillante .

SERIE DI MENGOLI-------- ----- ------ -------- ----- ------ ----- ----- ---------------

_{+ ∞}

1 .

_n=1 n ( n + 1 )

È una serie particolare che ci può fare da riferimento per determinare il carattere di altre serie.

Andiamo a studiarla nel seguente modo:

1) scomponiamo il termine generale per vederne il comportamento:

a_n = 1 . = 1 + n - n = 1 + n - n = 1 - 1 .

n ( n + 1 ) n ( n + 1 ) n(n+1) n(n+1) n n + 1

2) osserviamo che il termine generale è riconducibile alla sottrazione di due termini

3) Calcolandone il limite con n tendente a +∞ otteniamo il valore finito 1 per cui possiamo

affermare che la serie risulta essere convergente.

SERIE GEOMETRICA-------- ----- ------ -------- ----- ------ ----- ----- -------------

Chiamiamo serie geometrica la somma di infiniti termini avente per termine generale è una potenza:

_{+ ∞}

∑ qⁿ = 1 + q +q² +.+ qⁿ + .

ⁿ⁼⁰

la cui base si indica con q e l'esponente con n. Si può notare che il rapporto tra uno dei termini della serie e il suo precedente è q che viene per questo detto ragione.

Se q = 0    la serie converge e ha per somma il valore 1.

Se q = 1    la serie diverge e ha la seguente forma: 1 + 1 + 1 + . + 1 + .

Se q = - 1 la serie è indeterminata e ha la seguente forma : 1 - 1 + 1 - 1 + 1 - 1 .

Per studiare il carattere della serie per gli altri valori di q , utilizziamo la seguente uguaglianza:

1 + q +q² +.+ qⁿ + . = 1 - q ⁿ⁺¹ .

1 - q

Da cui ricaviamo, calcolandone il limite per n tendente a infinito, l'espressione:

1 .

1 - q

E quindi abbiamo i seguenti casi:

  se |q| <1 cioè -1 < q < 1 la serie è convergente

  se q < - 1 e q > 1 la serie è divergente

CRITERIO DI CAUCHY-------- ----- ------ -------- ----- ------ ----- ----- -----------

Criterio di Cauchy o condizione necessaria per la convergenza :

Tutte le serie convergenti hanno il termine generico infinitesimo, ovvero il limite per n che tende a infinito di An tende a 0.

Si tratta di una condizione necessaria ma non sufficiente in quanto non vale il contrario. Infatti esistono serie il cui termine generale è infinitesimo ma non sono convergenti.

SERIE ARMONICA-------- ----- ------ -------- ----- ------ ----- ----- -----------------

La serie armonica è la serie costruita sommando i reciproci dei numeri interi positivi, ovvero:

_{+ ∞}

∑ 1 .

ⁿ⁼⁰ n

ed è una serie divergente. Il termine generale è infinitesimo per n->∞ perciò la serie armonica è un chiaro esempio del teorema di Cauchy , ed anch'essa esprime una condizione necessaria, ma non sufficiente per la convergenza di una serie.

PRIMO CRITERIO DEL CONFRONTO-------- ----- ------ -------- ----- ------ -

Date le due serie a termini positivi :

_{+ ∞ + ∞}

∑ a_n e ∑ b_n

^{n=1 n=1}

sia, per n ≥ 1

a_n ≤ b_n

_{( minorante ) ( maggiorante)}

1) se la serie maggiorante è convergente, allora anche la serie minorante è convergente e

la somma della a_n è minore o uguale alla somma della b_n.

2)se la serie minorante è divergente, allora anche la serie maggiorante è divergente.

CRITERIO DEL RAPPORTO-------- ----- ------ -------- ----- ------ ----- ----- ----

Data la serie a termini positivi:

_+∞

∑ a_n = a₁ + a₂ +.+ a_n +.

ⁿ⁼¹

se esiste finito il limite

lim a_n + 1

ⁿ a_n

allora:

la serie converge se 0 ≤ l < 1

la serie diverge se l > 1

se il limite non esiste, o ha valore 1, il criterio del rapporto non fornisce alcuna indicazione sul

carattere della serie in esame.

CRITERIO DELLA RADICE-------- ----- ------ -------- ----- ------ ----- ----- -----

Data la serie a termini positivi:

_+∞

∑ a_n = a₁ + a₂ +.+ a_n +.

ⁿ⁼¹

se esiste finito il limite

lim ⁿ √ a_n

ⁿ

allora:

la serie converge se 0 ≤ l < 1

la serie diverge se l > 1

se il limite non esiste, o ha valore 1, il criterio del rapporto non fornisce alcuna indicazione sul

carattere della serie in esame.