|
|
| |
NOZIONI INTRODUTTIVE E NOZIONI
GLI INSIEMI
L'insieme è come una collezione qualsiasi di oggetti, in numero finito o infinito.
In un insieme finito il n° degli oggetti che lo costituiscono si dice anche ordine; un insieme infinito si dice anche di ordine infinito. Gli oggetti che costituiscono un insieme sono detti i suoi elementi.
Gli insiemi sono indicati con lettere maiuscole dell'alfabeto; gli elementi con lettere minuscole.
Per indicare l'appartenenza o meno dell'elemento x all'insieme A si scrive "x Є A" e "x Є A
L'insieme privo di elementi è detto insieme vuoto, indicando con il simbolo 0.
N è l'insieme dei n° naturali
Z è l'insieme dei n° interi relativi
Q è l'insieme dei n° razionali, cioè le frazioni n/m dove n e m sono n° interi relativi e m ≠ 0
R è l'insieme dei n° reali
C è l'insieme dei n° complessi
Simboli:
significa "per ogni";
significa "esiste almeno un/o/a";
! significa "esiste uno ed un solo";
![]() si legge "implica";
si legge "implica";
![]() si legge "se e
soltanto se";
si legge "se e
soltanto se";
![]() Esempio: p q significa che p e q sono
equivalenti;
Esempio: p q significa che p e q sono
equivalenti;
si legge "e";
V si legge "o".
SOTTOINSIEMI
Un insieme A si dice sottoinsieme dell'insieme B se ogni elemento di A appartiene a B.
Si scrive A ≥ B e si legge "A contenuto in B" o "A incluso in B". in simboli:
![]()
![]() A B (x Є A x
Є B)
A B (x Є A x
Є B)
OPERAZIONI TRA INSIEMI
Definizione: Dati 2 insiemi A e B, si dice insieme unione di A e di B l'insieme AUB avente come elementi gli oggetti che appartengono ad almeno uno tra A e B.
A B =
Definizione: Dati 2 insiemi A e B, si dice insieme intersezione di A e di B l'insieme A B avente come elementi gli oggetti che appartengono sia ad A che a B.
A ∩ B =
Esempio:
=
∩ =
2 insiemi A e B, si dicono disgiunti se non hanno elementi in comune, cioè A B = 0
Definizione: Dati 2 insiemi A e B, si dice insieme differenza di A e di B l'insieme A\B avente come elementi gli oggetti che appartengono ad A e non a B.
A \ B =
Esempio:
\ =
Se la differenza viene effettuata tra un insieme X e un suo sottoinsieme A, si parla di complementare del secondo insieme nel primo, denotata Сx (A)
![]() Definizione: Dati 2 insiemi A e B, si dice differenza simmetrica di A e di B
l'insieme A B avente come elementi gli oggetti che appartengono ad A e non a B e gli
oggetti che appartengono a B e non ad A.
Definizione: Dati 2 insiemi A e B, si dice differenza simmetrica di A e di B
l'insieme A B avente come elementi gli oggetti che appartengono ad A e non a B e gli
oggetti che appartengono a B e non ad A.
![]() A B = U = (A\B) (B\A)
A B = U = (A\B) (B\A)
![]() Esempio: = =
Esempio: = =
Definizione: Dati 2 insiemi A e B non vuoti, si dice insieme prodotto cartesiano di A e di B l'insieme A x B avente come elementi le coppie ordinate di elementi di A e di B.
A x B =
Esempio: Se A = e B = , si ha:
A x B =
CORRISPONDENZE E FUNZIONI
Funzione: E' una relazione che lega 2 grandezze fisiche, economiche o qualitative attraverso una legge matematica. Queste 2 variabili verranno chiamate x e y.
x viene detta variabile indipendente;
y viene detta variabile dipendente, perché dipende dalla x, per cui: y = f (x)
Dominio: L'insieme delle x si chiama dominio di funzione o campo di esistenza; ed è l'insieme di tutti i valori di x per i quali è possibile calcolare il valore della funzione, la variabile di x si chiama dipendente.
![]()
![]()
![]() Funzione Denominazione Dominio Esempio
Funzione Denominazione Dominio Esempio
y = mx + q funz. lineare D = y = 2x - 5
D =
y = ax2 + bx + c funz. quadratica D = y = 2x2 - 3x - 1
D =
N(x) x3 - 2x + 1
![]()
![]() y = funz.
algebrica D = y =
y = funz.
algebrica D = y =
D(x) fratta x2 - 3
D =
![]()
![]()
![]() y = n√f(x) funz. irrazionale
"n" pari D = y = x2 - 3
y = n√f(x) funz. irrazionale
"n" pari D = y = x2 - 3
D =
![]()
![]() "n" dispari D = y = 3 x + 4
"n" dispari D = y = 3 x + 4
D =
y = log x funz. logaritmica D = y = log (x2 - 1)
D =
y = ex funz. esponenziale il D di questa funz. coincide y = ex2+3x
con quello dell'esponente D =
y = sin f(x) sin[(x2 +2x -7)3(x -2)]
y = cos f(x) funz. goniometrica il D di queste funz. coincidono D =
![]()
![]()
![]() y = tg f(x) con
quello del loro argomento
y = tg f(x) con
quello del loro argomento
sin x2 +2x -8
D =
Esempi: y = 3x + 2 → D = V x Є R
y = 2√2x - 1 → essendo pari → D = 2x ≥ 1 → x ≥ 1/2 → D = V x Є R: x ≥ ½
y = 3√2x - 1 → essendo dispari → D = V x Є R
4x2 - 2
![]() y = → x + 2
≠ 0 → x ≠ -2 → D = x Є R: x ≠ -2
y = → x + 2
≠ 0 → x ≠ -2 → D = x Є R: x ≠ -2
x + 2
y = loga (1 - x) → 1 - x > 0 → x < 1 → D = x Є R: x < 1
y = e-x^2 → D = x R
Codominio: l'insieme delle y si chiama codominio, le variabili di y si chiamano variabili dipendenti.
Definizione: Una funzione è detta:
Iniettiva: se ogni elemento di A ha al più una controimmagine in B;
A B
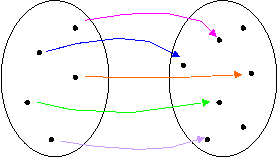
Suriettiva: se ogni elemento di A ha almeno una controimmagine in B;
A B
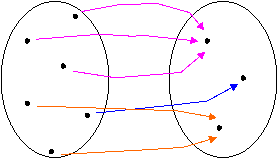
Biunivoca: se è sia iniettiva sia suriettiva; quindi se ad ogni punto di A corrisponde un punto di B.
A B
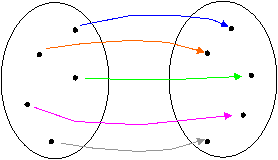
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025