ed è detto derivata prima di f in x₀.

Osservazioni:

Il rapporto

si chiama rapporto incrementale di f relativo a x₀.

Poiché è lecito porre x=x₀+h, se si ha che e dunque si può equivalentemente scrivere

Se si considera il limite per  () si parla di derivata destra e si indica con f'₊(x₀). Analogamente si definisce la derivata sinistra, che si indica con f'_-(x₀).

Si dimostra che f è derivabile in x₀ se e solo se f'₊=f'_-=f'.

Si dice che f è derivabile in un intervallo A se lo è in ogni punto di A.

Esempi:

v La funzione f(x)=k con k costante è derivabile in ed f'(x)=0 per ogni x in . Infatti si ha

v La funzione f(x)=x è derivabile in ed f'(x)=1 per ogni. Infatti

v Ogni funzione lineare f(x)=ax+b, , è derivabile in ed f'(x)=a per ogni. Infatti

Controesempio

v La funzione f(x)=|x| è derivabile per ogni x di diverso da zero. Infatti

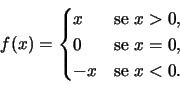
Allora

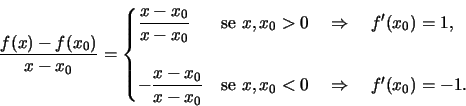
Considerando x₀=0 si ha

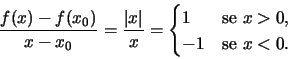
Quindi f'₊(0)=1, mentre f'_-(0)=-1 e dunque f non è derivabile in zero (esso è detto punto angoloso).

Vale il seguente importante teorema:

Teorema   Se f è derivabile in x₀, allora f è continua in x₀.

Osservazione   Il teorema stabilisce la relazione fra la continuità e la derivabilità di una funzione. Vale la pena di sottolineare il contenuto del Teorema, poiché si tende spesso a dar per scontata proprio la parte non vera: nelle ipotesi del teorema, la derivabilità di f(x) (in un punto x₀ o in un intero intervallo I) implica la sua continuità (nello stesso punto x₀ o nello steso intervallo I), ma non vale il viceversa: ad esempio f(x)=|x| è continua in x₀=0, ma è ivi non derivabile. Brevemente, si usa spesso scrivere

Un'ulteriore precisazione: quanto detto significa che dalla continuità non si può dedurre la derivabilità, ma non significa che una funzione continua non possa essere anche derivabile. Anzi, la maggior parte degli esempi di funzioni che incontriamo in questo libro sono funzioni continue e derivabili in tutto il loro dominio di definizione.

Infine si noti che se una funzione non è definita in un punto o in un intervallo, allora non ha senso parlare della sua continuità e/o derivabilità in quel punto o in quell'intervallo, semplicemente perchè essa ivi non esiste.

Significato geometrico di derivata

Per introdurre graficamente il concetto di derivata, fissiamo un punto x₀nel piano cartesiano che appartenga all'insieme di definizione di y=f(x) e consideriamo il punto P₀(x₀,f(x₀)) che appartiene al grafico G_f della funzione. Consideriamo inoltre un nuovo punto P(x,f(x)) sul grafico di f, distinto da P₀, la cui ascissa x appartenga ancora all'insieme di definizione di f. Per come abbiamo scelto le cose (figura 3.1) la retta s passante per P₀ e Pè una secante del grafico di f.

Fissato P₀, immaginiamo di poter avvicinare P a P₀sul grafico G_f: la posizione della retta secante cambia progressivamente fino a raggiungere una posizione limite quando P coincide con P₀: quella della retta t tangente al grafico di f in P₀ (figura 3.2. )

Il coefficiente angolare della retta secante s è

e lo si rappresenta mediante il rapporto degli incrementi e . Questa frazione è nota come rapporto incrementale di f(x) in x₀. Nel caso in esame, al tendere di P a P₀ si ha che tendono a zero sia la differenza (cioè la distanza di x da x₀), che la differenza (cioè la distanza di f(x)da f(x₀)). Portando il ragionamento al limite, si deve calcolare il limite del rapporto incrementale

Se questo limite esiste esso è chiamato derivata di f in x₀ ed è dunque il coefficiente angolare della retta tangente t al grafico di f in P₀.

Precisazioni sul significato geometrico

Abbiamo dimostrato che se f è derivabile in (a,b) allora è anche continua in (a,b): quindi G_f è un arco di curva continua nel piano cartesiano ed è perciò lecito in fig. 3.1 immaginare di poter avvicinare P a P₀.

Pertanto se f è derivabile in x₀, allora geometricamente esiste la retta tangente a G_f in P₀, di coefficiente angolare finito dato da (fig3.2) L'equazione di tale retta è:

dove il termine noto q=f(x₀) si ottiene immediatamente da

Osservazioni:

Il secondo membro della (3.2) può essere usato per approssimare la funzione f(x):

Tale approssimazione è detta approssimazione del prim'ordine (fig.3.3) Il valore a secondo membro di (3.2) approssima tanto meglio f(x) quanto più x è vicino ad x₀ (poichè in x₀ si ha

Se

per definizione f non è derivabile in x₀, ma geometricamente esiste ugualmente la retta tangente a G_f in (x₀,f(x₀)) ed è una retta parallela all'asse delle ordinate. Si dice in questo caso che f ha un flesso a tangente parallela all'asse delle ordinate, ossia a tangente verticale.   

Due applicazioni importanti della nozione di derivata, come accennato all'inizio del capitolo, sono la nozione di velocità e quella di accelerazione in meccanica.

Calcolo della derivata

Teorema (Regole di derivazione)   Siano f e g due funzioni derivabili in e k una costante: allora

sono derivabili in x₀s e valgono le seguenti relazioni:

i)

,

ii)

(fg)'(x₀)=f'(x₀)g(x₀)+f(x₀)g'(x₀),

iii)

(kf)'(x₀)=kf'(x₀),

iv

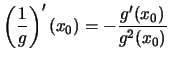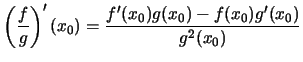(per ),v) (per ).

Le formule date nel teorema 9per una coppia di funzioni si estendono al caso di n>2 funzioni.

Esempi:

La funzione f(x)=xⁿ, , è derivabile per ogni x₀ e la derivata è

f'(x₀)=nx₀^n-1.

Più in generale, se la funzione è un polinomio di grado n si scrive

Ad esempio è Dx³=3x².

La derivata del reciproco di una potenza, cioè di , si ottiene da v) e risulta

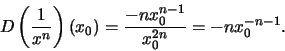
Così ad esempio Dx^-3=-3x^-4.

Esercizi: .

Calcolarein x₀, ove .
Soluzione:

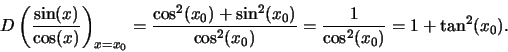
Dire se la funzioni ed sono derivabili e determinarne la derivata.
Soluzione: sono derivabili come prodotto di funzioni derivabili e si ha

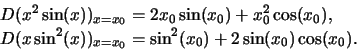
Determinare la retta tangente al grafico di nel punto di ascissa uguale a uno.
Soluzione:

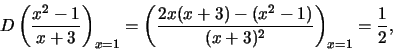
allora

Teorema (Derivata della funzione composta)   Se f(x) e g(x) sono funzioni derivabili e ha senso considerare , allora tale funzione composta è derivabile in x₀(g lo è in f(x₀)) e risulta

La formula (3.3) è anche nota come regola della catena.

Esempi:

Per la funzione , ponendo f(x)=y=ax+b e , si ottiene

.

.

.

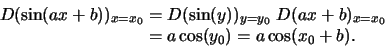
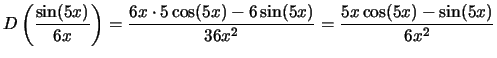Teorema (Derivata della funzione inversa)  

Sia f invertibile e sia f^-1 l'inversa. Se f è derivabile in x₀ con , allora f^-1 è derivabile in y₀=f(x₀) e

dove x₀=f^-1(y₀). 

Geometricamente, l'equazione (3.4) dice che il coefficente angolare della retta tangente al grafico della funzione inversa f^-1 nel punto Q di coordinate (y_Q,f₁(y_Q))=(f(x_P),x_P), è il reciproco del coefficente angolare della retta tangente al grafico di f(x) nel generico punto P(x_P,f(x_P)), cioè (fig. ):

Esempi:

Consideriamo , che è l'inversa di y=x²: allora

Per la funzione potenza y=xⁿ l'inversa è , quindi

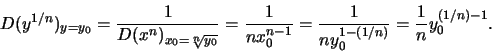
La funzione è l'inversa di , , , allora

Questo risultato discende dal fatto che per e dunque dalla relazione trigonometrica fondamentale si ricava

Analogamente, poiché è l'inversa di si ha

Esercizi:

Sono derivabili in x₀=0 le funzioni e ? Suggerimento: sia f che g sono funzioni composte: calcolando i limiti a destra e a sinistra del rapporto incrementale per f(x) si ha che valgono . Pertanto 0 è un punto dove esiste un flesso a tangente verticale. Per g(x) i due limiti valgono rispettivamente e : in tal caso si dice che 0 è un punto cuspidale.

Osservazione   Se la derivata di f è una funzione derivabile, si può considerare la derivata di f': tale funzione si indica con f'' e si chiama derivata seconda di f, o anche derivata del second'ordine di f. Se f è derivabile tre volte (cioè se anche f''è derivabile) allora possiamo considerare la funzione f''', che si chiama derivata terza di f, e così via.

Esempio:

Le funzioni e sono entrambe derivabili risulta:

ossia sono entrambe derivabili infinite volte. Per le funzioni potenza con esponente intero risulta

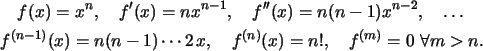
In pratica, la derivata di ordine n di una potenza n-esima è la costante n! e tutte le derivate di ordine superiore ad n sono nulle. Ad esempio