|
|
| |
LE EQUAZIONI DIFFERENZIALI
INTRODUZIONE
Un'equazione differenziale è un'equazione matematica avente come incognita una funzione y =f (x), che definisce una relazione tra x, y e le derivate successive di y, calcolate rispetto alla variabile x.
Una equazione differenziale è detta di ordine n quando stabilisce una relazione tra y, x e le prime n derivate di y rispetto a x; nel caso più generale, essa può essere espressa nella forma:
F (x, y, y', y'', ... , yn) = 0
Risolvere, o integrare, un'equazione differenziale significa trovare tutte le sue soluzioni, ovvero quelle funzioni che verificano l'uguaglianza; esse sono infinite e dipendono da un numero di costanti pari all'ordine n dell'equazione stessa.
L'insieme di tutte le soluzioni è detto Integrale Generale espresso come:
y = Φ (x,c1,c2....cn)
Ogni funzione che si ottiene dall'integrale generale assegnando particolari valori alle costanti c1,c2....cn viene chiamata Integrale particolare.
TEOREMA DI CHAUCHY
Se la funzione f(x,y) e la sua derivata parziale ![]() sono continue nei
punti interni ad un certo dominio D e se
sono continue nei
punti interni ad un certo dominio D e se ![]() è un punto interno a D, allora esiste une ed una sola
soluzione dell'equazione:
è un punto interno a D, allora esiste une ed una sola
soluzione dell'equazione:
![]()
definita in un certo intorno di x0, per la
quale risulta ![]() cioè per il punto
cioè per il punto ![]() passa una sola curva
integrale dell'equazione.
passa una sola curva
integrale dell'equazione.
EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE
Si definisce equazione differenziale del primo ordine un equazione del tipo:
F (x,y,y') = 0
Nella quale la x e la y possono anche non comparire , mentre la y' deve esplicitamente figurare (altrimenti l'equazione non risulterebbe di natura differenziale.
Prendiamo in esame 5 tipi di equazioni differenziali del primo ordine con i rispettivi metodi per la risoluzione:
METODI DI RISOLUZIONE DI EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE
EQUAZIONI A VARIABILI SEPARABILI
Questo tipo di equazioni hanno la proprietà di ridursi alla seguente forma:
![]()
Essendo:
![]() si ottiene che:
si ottiene che:![]()
Dividendo i due membri per g(y) e integrando si ottiene il valore di y:
![]()
ESEMPIO 1

EQUAZIONI LINEARI
Prende il nome di equazione differenziale lineare quella equazione che è di primo grado rispetto alla funzione incognita y e alla sua derivata prima y'; può essere scritta così:
![]()
Dove f(x) e g(x) sono funzioni continue della variabile x in un intervallo [a,b]:
Posto,
![]()
L'integrale generale è dato dalla relazione:
![]()
ESEMPIO 2

EQUAZIONI OMOGENEE
Si chiama equazione differenziale omogenea del primo
ordine, un'equazione che si può scrivere sotto la forma:![]() .
.
Per risolverla si pone:
![]() ovvero
ovvero ![]() la cui derivata
è
la cui derivata
è ![]()
Sostituita nell'equazione si ottiene: ![]()
![]() un'equazione a
variabili separabili.
un'equazione a
variabili separabili.
ESEMPIO 3
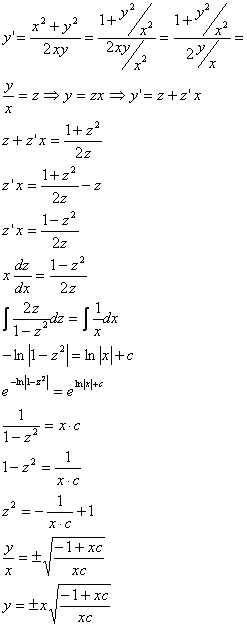
EQUAZIONI DI BERNOULLI
E' definita equazione di Bernoulli un'equazione differenziale del primo ordine che si può ricondurre alla forma:
![]()
Le funzioni f(x) e g(x) sono continue in un certo intervallo [a,b].
Si può essere trasformata in un equazione lineare di primo grado, dividendo entrambi i membri per ya:
![]()
si pone: ![]()
sostituendo si ottiene: ![]()
ESEMPIO 4
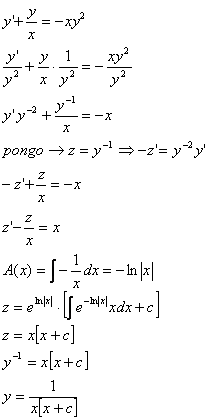
EQUAZIONI ESATTE
Un'equazione del primo ordine del tipo:
![]()
con M(x,y) ed N(x,y) due funzioni
continue, insieme alle loro derivate parziali prime, in un intorno R del punto ![]() , si dice esatta quando il suo primo membro è esatto, ovvero
quando risulta:
, si dice esatta quando il suo primo membro è esatto, ovvero
quando risulta:
![]() , in tutti i punti
interni ad R.
, in tutti i punti
interni ad R.
Il suo integrale generale è dato dalla funzione:
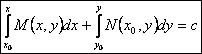
EQUAZIONI DIFFERENZIALI DEL SECONDO ORDINE
Si definisce equazione differenziale del secondo ordine un equazione del tipo:
F (x,y,y',y'') = 0
Nella quale la x, la y e la y' possono anche non comparire , mentre la y'' deve esplicitamente figurare (altrimenti l'equazione non risulterebbe del secondo ordine, ma di uno inferiore o del tutto non differenziale.
EQUAZIONI OMOGENEE A COEFFICIENTI COSTANTI
Sono equazioni del tipo:
![]()
con a, b e c costanti reali.
Per determinare l'integrale generale si risolve un'equazione di 2° grado, detta "equazione caratteristica dell'equazione differenziale", avente per coefficienti a, b e c:
![]()
Ricordando che un'equazione di II grado può avere soluzioni:
o REALI E DISTINTE
o REALI E COINCIDENTI
o COMPLESSE CONIUGATE
si distinguono i 3 casi.
In questo caso l'integrale generale dell'equazione differenziale è dato da:
![]()
ESEMPIO
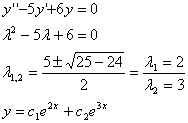
In questo caso l'integrale generale dell'equazione differenziale è dato da:
![]()
ESEMPIO
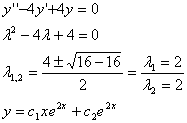
In questo terzo caso le soluzioni della equazione differenziale sono di natura complessa, ovvero costituite da una parte reale e una parte immaginaria.
Trovate le due soluzioni:![]()
Si scrive l'integrale generale:
![]()
ESEMPIO
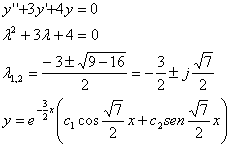
EQUAZIONI NON OMOGENEE A COEFFICIENTI COSTANTI
Sono equazioni differenziali del tipo:
![]()
Nella quale g(x) viene detto "termine forzante".
L'integrale generale è dato dalla formula:
![]()
Dove ![]() è l'integrale generale
dell'equazione omogenea associata:
è l'integrale generale
dell'equazione omogenea associata:![]() e
e ![]() è un integrale
particolare.
è un integrale
particolare.
Nel caso in cui g(x) è un polinomio di grado n l'integrale particolare, è:
ESEMPIO SPIEGAZIONE

Si sostituisce nell'equazione originaria
Si confrontano i risultati
Non compare nessun valore per c quindi esso può assumere qualsiasi valore
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025